UWB MIMO近场成像雷达稀疏阵列设计方法研究
2019-10-16张小虎苏卫民
张小虎 顾 红 苏卫民
(南京理工大学 南京 210094)
0 引言
近年来,由于在藏匿武器的检测、穿墙成像、地质勘探、以及倍受关注的医疗诊断等领域有着广泛的应用和社会市场需求,雷达近场成像[1-5]受到越来越广大的关注。在大部分的近场成像应用中,主要是对小场景进行成像,对成像分辨率的要求高。例如在藏匿武器的检测应用中,须要对距离天线约为0.5m,成像区域大小为0.5×0.5m场景进行成像,成像系统在2个维度方向都要达到1~2cm的分辨率。遵循奈奎斯特空间采样定理,均匀阵列的阵元间距应满足小于或等于半波长(λ/2),以抑制不希望的栅瓣产生[6]。同时为了达到cm级分辨率,设计的阵列天线的有效孔径长度至少要为波长的50倍,天线孔径至少需要101个阵元数目来填充。不幸的是,制造如此密集的阵列将带来巨大的开销,以及需求很高的制作工艺,并且庞大的阵元数意味着较大的数据流,使得需要消耗大量的硬件资源来处理和计算接收到的回波数据,实时成像变得难以实现。
因此在达到相同的分辨率的情形下,阵列稀疏的和较少的阵元使用数目成为了设计近场高分辨成像系统的目标。但是阵列的稀疏会导致栅瓣的产生,于是最典型的抑制栅瓣的方法是设计非周期阵或随机阵[7],这样可以将栅瓣的能量分散到整个天线孔径当中去。尽管非周期阵列不会产生栅瓣,但是这种方法设计的稀疏阵列往往会遭遇到旁瓣高的问题[6]。利用多发多收(MIMO)方式是来实现阵列稀疏的一条好途径,Zhuge[8]利用MIMO阵列的等效孔径在近场中很大程度等于发射孔径和接收孔径的卷积特性,将设计稀疏MIMO阵列的任务,分解成了单独设计发射子阵和接收子阵的任务,然后通过合成设计的子阵来得到没有冗余统一加权的等效阵列。使用超宽带信号(UWB)来替换原有的窄带发射信号也是实现阵列稀疏的一个方法,Schwartz[9]定义了判定阵列稀疏的标准为d≥cT(d为阵元间距、c为电磁波的传播速度、T为发射脉冲信号的持续时间),提出了在宽带脉冲信号的激励下,发射的波形只会在天线主瓣附近发生干涉,并将该区域命名为干涉区(IR)。阵列孔径越大,UWB脉冲持续时间越短,阵列越稀疏,则干涉区(IR)会变得越小,成像系统的分辨率也会越高。Anderson[10]更加指出利用超宽带阵列进行成像时,为了增加成像的分辨率,可以简单的将阵列中的阵元间距拉大,而不需考虑栅瓣产生的问题。
UWB技术可以极大地提高成像的分辨率,MIMO使得阵列设计更加灵活和稀疏,将UWB与MIMO结合的成像技术也开始越来越受到广范地研究,但是到目前为止,UWB MIMO近场高分辨成像雷达的阵列设计方法和理论还不够完善。本论文针对以上问题,提出了一种基于等效相位中心原理(PCA)的UWB MIMO近场成像雷达稀疏阵列的设计方法。由于等效相位中心的近似会造成误差的产生,误差在天线远场区可以忽略不计,但在天线近场区,影响会变得尤为突出,因此须要对误差进行了相应的补偿。随后,论文通过数值仿真工具(FDTD)进行仿真,考察了阵列的波束方向图,并分别对单个点目标和分布式目标进行成像,仿真结果验证了该阵列设计方法的有效性和应用于近场高分辨成像的可行性。
1 等效相位中心原理与误差补偿
假设MIMO雷达有M个发射阵元、N个接收阵元,目标的分布函数为o(x0,y0),任一发射阵元的坐标为(xt,m,yt,m),任一接收阵元的坐标为(xr,n,yr,n),两阵元间距为lm,n,如图1所示。Rt,m和Rr,n分别表示为发射阵元到目标的距离和接收阵元到目标的距离,它们的直角坐标表示形式为:
(m=0,1,…,M-1)
(1)
(n=0,1,…,N-1)
(2)
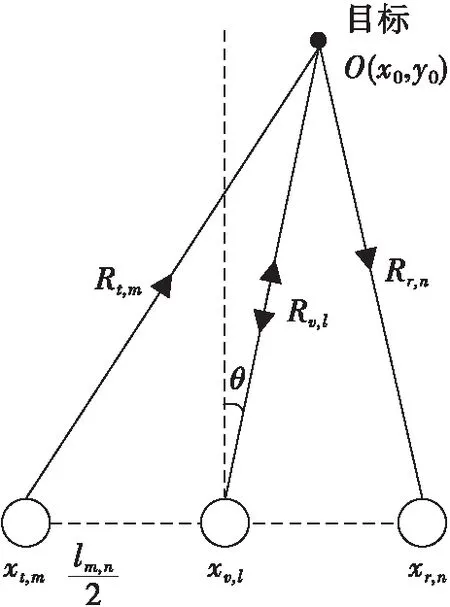
图1 等效相位中心示意图
等效相位中心近似原理是用一个虚拟阵元来近似代替一对发射接收分置的阵元,虚拟阵元位于发射和接收阵元连线的中心位置,图1中,xv,l为虚拟阵元位置,虚拟阵元到目标的距离可以表示为:
(l=0,1,…,MN-1)
(3)
用一个虚拟阵元来近似代替一对发射接收分置的阵元会带来路程差,定义路程差为:
ΔR(lm,n,Rv,l,θ)=Rt,m+Rr,n-2Rv,l
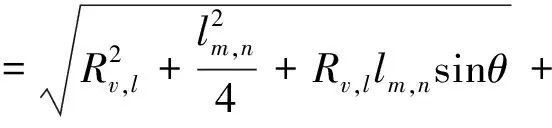

(4)
式(4)中,θ为虚拟阵元到目标之间的连线与阵列法线方向的夹角。在远场条件下,目标与虚拟阵元之间的距离Rv,l远大于发射和接收阵元之间的距离lm,n,路程差ΔR≈0或ΔR≤λ/4,对应的相位误差小于π/2。因此在远场条件下,使用等效相位中心近似处理带来的误差可以忽略不计。但在近场条件下,不再满足Rv,l≫lm,n的关系,近似处理带来的误差不再可以忽略。
图2给出了当采用发射信号频率为10GHz、θ角为0°、目标与虚拟阵元的距离Rv,l为0.5m时,ΔR关于lm,n的变化曲线图。由于在θ角为0°时,路程差ΔR最大,因此本文后面的讨论中,都只讨论θ角等于0°时的情形。图中虚线的值为λ/4,由图中可以看出,当lm,n>0.125m时,曲线ΔR已经和虚线相交,路程差造成的相位误差已经大于π/2。使用等效相位中心原理设计满足近似路程差小于λ/4的阵列天线,lm,n的取值范围直接决定着天线的最大孔径,如果是SIMO雷达,天线的孔径最大可以设计为2·(lm,n)max,如果是MIMO雷达,天线最大孔径要小于(lm,n)max。使用孔径为0.125m的MIMO阵列对0.5m处的目标成像,很难达到1~2cm的成像分辨率, 因此须要对等效相位中心近似产生的误差进行补偿校正,来扩大lm,n的取值范围。

图2 发射信号频率为10GHz、θ角为0°、Rv,l为0.5m时,ΔR关于lm,n的变化曲线
将ΔR展开为关于lm,n的二阶泰勒级数,用作路程差补偿项:
(5)
采用ΔR的二阶泰勒级数来校正等效相位中心的路程差,产生的近似误差[11]可以表示为:
(6)
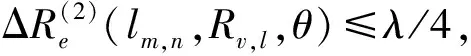

图3 发射信号频率为10GHz、θ角为0°、Rv,l为0.5m时,关于lm,n的变化曲线
2 UWB MIMO阵列的设计
本文主要是针对检测人身上携带藏匿武器的应用,来设计的UWB MIMO稀疏线阵。在该应用场景中,目标距离天线大约为0.5~1m,为了能识别出大部分的藏匿武器或危险品,成像系统需要达到1~2cm的分辨率。由于本文设计的是线阵,只能重构出距离和方位的二维像,要得出目标的三维像,需要机械带动线阵在垂直方向对目标进行扫描。本文先只研究设计的线阵在距离向和方位向的成像效果。
2.1 UWB信号的选择
信号带宽、中心频率、天线的孔径大小以及潜在目标的距离都是影响近场成像雷达成像分辨率的因素。距离向的分辨率主要是受信号带宽的影响,计算公式为:
(7)
其中B为信号的-10dB带宽,c为光的传播速度。方向维的分辨率受信号带宽影响很小,主要由信号的中心频率和天线的孔径大小来决定,计算公式为:
(8)

综合以上考虑,采用广义的高斯脉冲信号(GGP),式(9)为信号的时域表达式,其中E0为在t0时刻脉冲的峰值幅度;α为尺度因子,它控制着脉冲信号的频谱;ΔT为脉冲的有效持续时间。当设计的MIMO阵列有效孔径长度约为1m时,选取发射信号的中心频率为10GHz,-10dB带宽为10GHz,根据公式(8)和公式(9)进行计算,对距离天线0.5m处目标进行成像,可以在距离向和方位向都实现1.5cm的分辨率。
(9)
2.2 MIMO阵列的布阵
根据2.1节分析得知,当发射信号的中心频率为10GHz(λc=0.03m)时,设计的MIMO阵列有效孔径长度要约为1m,才能实现方位向1.5cm的分辨率。并且根据第二章节的分析,使用ΔR的二阶泰勒级数来校正等效相位中心造成的路程差时,阵列中发射和接收阵元距离lmn最大为0.51m。本文使用等效相位中心原理来设计稀疏阵,希望实际物理阵元之间间距能尽量的拉大,但产生的均匀虚拟阵阵元间距仍然小于或等于λc/2,以满足奈奎斯特空间采样定理。根据以上约束条件,阵列的布阵方式如下:
1)确定发射阵元数M和接收阵元数N;
2)接收阵元均匀分布,阵元的间距ΔRx;
3)两发射阵元对称分布于接收阵元的两侧,阵元间距为(N-1/2)ΔRx;
4)为了增加虚拟阵元的分布密度,可以在发射阵元中加入子阵,子阵中阵元的间距为ΔRx/nsubTx,nsubTx为每一个子阵中发射阵元的个数。最后设计出的MIMO阵列,虚拟阵元间距为ΔRx/(2·nsubTx),且均匀分布无重叠。

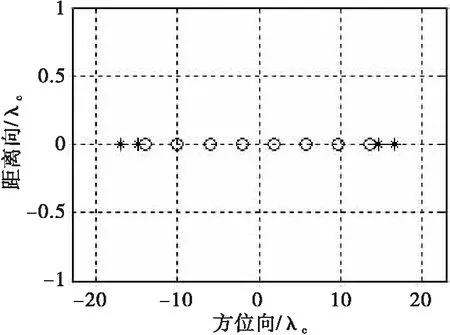
图4 MIMO阵列拓扑结构

图5 虚拟阵列示意图
3 成像算法
本文使用Kirchhoff偏移算法[12]来对目标进行成像。在均匀各向同性的介质当中,将原本向量类型的波动方程简化为标量波动方程,使得Kirchhoff偏移算法可以用来研究和计算电磁波的传播。Kirchhoff偏移算法的基本原理是,将接收平面接收到的时域电磁波信号,反向传播至目标所在的平面,然后对电磁波的标量波动方程做积分。
Kirchhoff偏移算法的基本公式为:
(10)
其中
(11)
式(10)中,u(r,t)为采集到的回波数据,Rv,l为等效阵元到目标的距离,θ为等效阵元到目标之间的连线与阵列法线方向的夹角,lm,n为发射阵元与接收阵元的距离,它们之间的几何关系如图1所示。r′为被偏移到的成像点坐标向量,r为回波数据采集点的坐标向量,v为电磁波的传播速度。式(11)中的第二项即为等效相位中心的误差补偿项。Kirchhoff偏移算法与后向投影算法(BP)相比,虽然计算量有一点点的增加,但是Kirchhoff偏移算法是从波动方程出发推导出来的,避免了BP算法一些不良的特性,更加适用于高分辨率成像应用中。
4 计算电磁仿真
为了验证设计的阵列成像性能,本文采用有限时域差分法(FDTD)来进行仿真。先来考察设计的阵列在近场条件下的波束方向图,获取阵列的近场方向图的方法是:选取广义的高斯脉冲信号作为发射信号,信号的中心频率为10GHz,-10dB带宽为10GHz,在阵列中心的正前方0.5m处,放置一个直径为1cm的球形散射体(球形散射体的大小小于阵列的横向分辨率即可),散射体的相对介电常数为4。然后使用Kirchhoff偏移算法,将所有接收到的回波数据进行聚焦,得到了二维点扩散函数(PSF)的图像。找寻PSF的图像最大值,并沿着方位向进行切割,得到的图像用来表示该阵列的近场波束方向图,如图6所示。
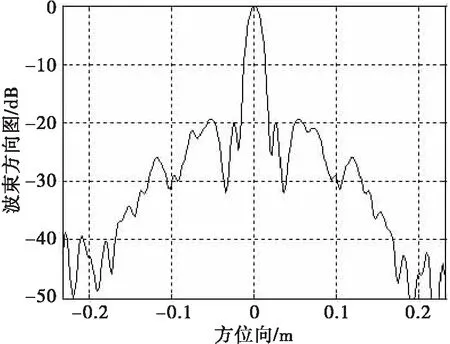
图6 阵列在近场区的波束方向图
图6中可以看出,在-3dB处,波束宽度为1.6cm,阵列的旁瓣大部分都在-20dB以下,在成像区域,没有出现明显的栅瓣,设计的阵列达到了预想的指标。图7为放置在阵列中心的正前方0.73m处,相对介电常数为4,电导率为0.01S/m的点目标成像效果图,显示的动态范围为-17dB,图中看不到旁瓣造成的虚影。图8展示了不补偿等效相位中心近似造成的路程差的情形,显然图像没有得到聚焦,可见采用ΔR的二阶泰勒级数作为误差补偿项是正确有效的。

图7 点目标的成像效果图

图8 不补偿路程差的散焦效果图
当对分布式目标进行成像时,情况会变得很复杂。来自于各个散射体的旁瓣相互混叠,如果旁瓣混叠得过高,则会形成错误的目标或者使得原本的目标形状发生改变。所以分布式目标的成像效果对阵列的旁瓣特性很敏感,下面来考察对分布式目标进行成像的情形。图9给出了目标的分布图,目标是沿着距离向分布的,构成目标的材料相对介电常数为4,电导率为0.01S/m。图10为分布式目标的成像效果图,显示的动态范围为-17dB,由于发射的电磁波大都被左半部平行于方位向的目标反射回去,所以基本上看不到分布式目标左上半部分的像,但被电磁波照射到的目标部分,得到了正确清晰的像。
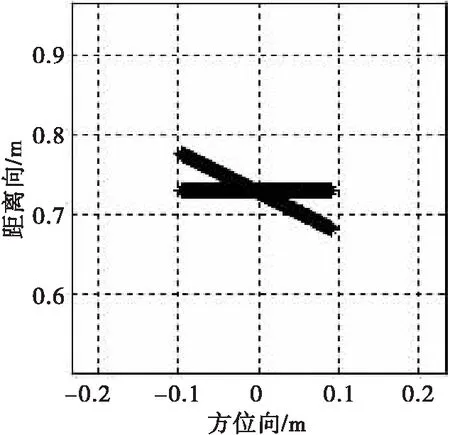
图9 目标分布图

图10 分布式目标的成像效果图
5 结束语
本文以近场高分辨成像为研究对象,提出了一种基于等效相位中心原理设计UWB MIMO近场成像雷达稀疏阵列的方法。文章首先分析了在天线的近场区域,等效相位中心近似产生的误差是不可忽略的,于是采用路程差的泰勒级数展开式做近似补偿。然后以藏匿武器检测成像的应用背景,给出基于等效相位中心原理设计UWB MIMO稀疏阵列的方法,该设计方法也可以用在其它应用背景中。最后论文通过数值仿真工具(FDTD)进行仿真,分析了设计的阵列波束方向图特性,并分别对单个点目标和分布式目标进行成像,仿真结果均符合设计指标,验证了该阵列设计方法的有效性和应用于近场高分辨成像的可行性。
