基于非渗透包装的米威化饼干二组分食品间水分扩散特性研究
2019-10-15程学雨钱奕含卢立新
程学雨 - 钱奕含 - 卢立新,2 -,2
(1. 江南大学,江苏 无锡 214122;2. 江苏省食品先进制造装备技术重点实验室,江苏 无锡 214122)
多组分食品日新月异,组分的不同会导致组分间水分扩散产生差异,对多组分食品间水分扩散的研究可为多组分食品的保质、防潮及货架期预测等提供借鉴[1]。多组分食品一般是由高、低两种不同水分活度的食品或高、中、低3种不同水分活度的食品组成,水分一般是由水分活度高的组分向水分活度低的组分扩散。
在食品储存保质研究中,国内外对水分扩散的研究主要集中在对单组分食品的研究和由单组分食品组合形成的多组分食品的研究,对真正在售的多组分食品水分扩散研究较少。王雪媛等[2]对苹果片短波干燥过程中水分扩散特性和玻璃化转变温度的变化规律进行了研究;陈思羽等[3]对玉米果穗水分迁移规律等进行了研究;李兴军等[4]利用重量法对大豆水分吸附速率和有效扩散系数进行了研究;Souraki等[5]通过对青豆在盐溶液中渗透过程的研究,建立了青豆水分和溶质扩散的数学模型;Shirkole等[6]利用物理化学特性对辣椒的吸附现象和水分迁移率进行建模。而对于由单组分食品组合形成的多组分食品,Chu等[7]对韧性饼干、猪肉脯及山楂片利用Fick第二定律解析模型求得水分扩散理论模型;陈亚慧等[8]通过对饼干和琼脂凝胶在非渗透条件下水分扩散研究,得到饼干的水分有效扩散模型,并进行了试验验证;郝发义[9]对饼干、果丹皮及凝胶的水分扩散系数模型进行了表征,并利用有限元分析对水分扩散过程进行了模拟;Jens[10]通过对含葡萄干、烤杏仁、花生和香蕉片二元或三元混合物的封闭系统中水分传递进行了研究;O" Connor等[11]对即食面包和美国干酪片间水分迁移的抑制进行了研究。对目前市场上在售的多组分食品如三明治、夹心饼干等的研究尚未见报道,对多组分食品水分扩散的研究仍停留在理论阶段,并未对在售食品进行实际研究,在售多组分食品因组分的特性、占比等不同,各组分间的水分扩散更为复杂。
试验拟对二组分食品—米威化饼干进行试验研究,结合其等温吸湿模型及水分有效扩散系数理论求解Fick第二定律微分方程,建立非渗透包装条件下二组分食品间的水分扩散模型,并通过水分吸附动力学试验对理论模型进行验证,为米威化饼干等同类的多组分食品防潮保质包装等研究提供技术支撑。
1 材料与方法
1.1 材料
米威化饼干:主要配料有小麦粉、乳糖、食用植物油、代可可脂巧克力制品、糯米粉、白砂糖、淀粉、乳粉,食品添加剂等,亿滋食品(北京)有限公司;
高阻隔性PET/AL/PE复合膜:上海易诺包装材料有限公司。
1.2 仪器与设备
恒温恒湿试验机:THS-AOC-100AS型,庆声科技有限公司;
电子分析天平:AB204-N型,梅特勒—托利多集团;
电热恒温鼓风干燥箱:DHG-9030A型,上海精宏实验设备有限公司;
有色印字连续封口机:FRW-1980型,中国华联机械有限公司。
1.3 方法
1.3.1 等温吸湿试验 在温度23 ℃、相对湿度0.35~0.90 条件下对米威化饼干中的馅料和饼皮分别进行等温吸湿试验,采用静态称重法称量各湿度阶段馅料和饼皮的重量,并计算平衡含水率,最后通过理论模型拟合得到等温吸湿模型。
1.3.2 饼皮水分有效扩散系数试验 划分10个相对湿度阶段,对3组样品进行试验,取平均值。预先准备好3套带盖有机玻璃容器,尺寸和饼皮尺寸相同,确保饼皮中水分为单方向扩散,分别称量3组样品的初始质量,计算得到3组样品的初始含水率X0,然后将玻璃容器及样品放入设置好初始条件的恒温恒湿箱中,在相对湿度条件为35%~45%,70%~80%时,每隔10 h进行称重并改变湿度条件,湿度条件为50%~65%时,每隔15 h进行称重并改变湿度条件,因饼皮在中高水性范围内吸水较多,故增加中高水分活度阶段的吸水时间,确保结果准确。动力学试验的条件设置如表1所示。分别计算该湿度阶段的平均含水率和平衡含水率,采用Crank[12]无限大平板模型计算各湿度阶段的扩散系数值Deff。
(1)

表1 饼皮水分吸附动力学试验的条件设置
式中:
X——平均含水率,g/g;
X0——初始含水率,g/g;
Xe——平衡含水率,g/g;
L——饼皮厚度,m;
t——时间,s。
1.3.3 饼皮和馅料间水分扩散模型的建立与验证 将馅料放置于有机玻璃容器的底部,饼皮至于馅料的上部,并用高阻隔性薄膜进行密封,降低环境湿度影响。非渗透包装条件下二组分食品间水分扩散的数学模型如图1所示。

图1 二组分食品间水分扩散的数学模型
Fick第二定律适用于均匀介质中物质的非稳态扩散过程,采用该定律进行二组分食品间水分扩散理论推导时,因两组分的水分活度相差大且扩散时间短,故高水分活度组分含水率不会发生显著变化,认为该组分的水分扩散系数为常数即D1恒定不变。故Fick第二定律可以表示为[13]:
(2)
(3)
式中:
X1——高水分活度组分馅料的含水率,g/g;
X2——低水分活度组分饼皮的含水率,g/g;
D1——高水分活度组分馅料的扩散系数,m2/s;
D2——低水分活度组分饼皮的扩散系数,m2/s;
e1——高水分活度组分馅料的厚度,m;
e2——低水分活度组分饼皮的厚度,m。
其中,D1不随含水率X1变化;D1随含水率X2的变化,可根据Tong & Lund经验模型[14]进行拟合:
(4)
式中:
ai——模型参数;
D0——模型参数;
n——常数,通常取1~5(根据拟合效果确定)。
通过采用线上法求解模型,三点中央差分法对原微分方程处理,Fick第二定律可以进一步表示为[7]:
(5)
(6)
在非渗透包装条件下水分沿厚度方向单向扩散,故该方程的初始条件和外界边界条件为:
X1(x,0)=X10,
(7)
X2(x,0)=X20,
(8)
(9)
(10)
式中:
X10——馅料的初始含水率,g/g;
X20——饼皮的初始含水率,g/g。
假设在水分扩散过程中两组分接触面上的水分活度瞬时达到平衡,两组分接触面的边界条件可以根据两组分的等温吸湿模型及水分迁移原理得到。
通过Matlab中ode15s算法结合式(2)~(8)及边界条件进行求解,可求得饼皮(X2)的含水率和时间的数值解。
非渗透包装条件下进行饼皮和馅料间水分扩散模型验证,采用高阻隔性铝箔复合膜和有机带盖玻璃容器创造密闭环境,试验过程中将样品放置于有机玻璃容器中并确保水分在二者间是单向扩散,然后将高阻隔性铝箔复合膜用热封机封口,再将密封好的样品放入温度为23 ℃ 的恒温恒湿箱中。因前期水分扩散较快,随着时间的推移水分扩散逐渐变慢,故前期测量时间间隔短,后期测量时间间隔长,分别计算出对应时间下的含水率。设3次平行试验,取平均值。
2 结果与分析
2.1 饼皮和馅料的等温吸湿模型
通过静态称重法及Matlab中Levenberg and Marqu-art算法对等温吸湿试验数据拟合,得到拟合曲线及对应的模型参数,结果表明最适合表征饼皮和馅料的等温吸湿模型分别为Lewicki模型和Peleg模型[15],两种模型的拟合相关系数分别为0.995 4,0.998 1,拟合效果好。拟合曲线分别见图2、3。
馅料的等温吸湿模型如式(11)。
X1=3.638(aw)43.35+0.067 29(aw)0.303 6。
(11)
饼皮的等温吸湿模型如式(12)。
(12)

图2 饼皮等温吸湿模型拟合曲线
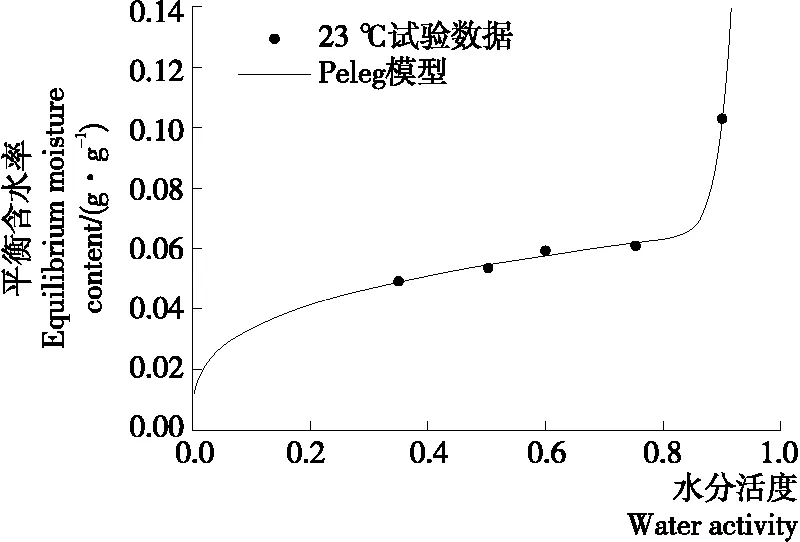
图3 馅料等温吸湿模型拟合曲线
2.2 米威化饼干饼皮的水分扩散系数模型
利用Crank无限大平板模型方程计算各湿度阶段的水分扩散系数,再利用Matlab中Levenberg and Marquart算法对含水率和水分扩散系数与Tong & Lund经验模型拟合,得出最适合表征饼皮水分扩散系数的模型,拟合曲线见图4。
结果表明,n=3时拟合效果最好,拟合指标R2=0.966 2,饼皮的水分扩散模型为:
Deff=1.657×10-11×exp(173.2X-763.3X2-200.7X3)。
(13)
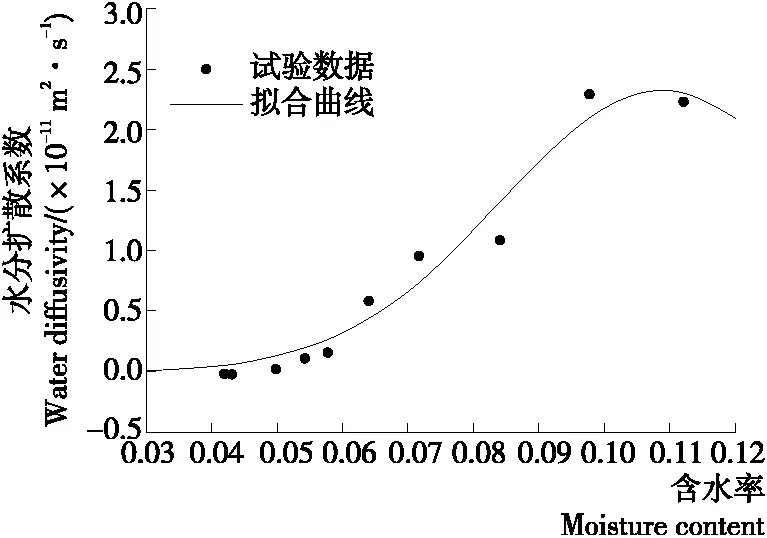
图4 饼皮水分扩散系数和含水率的关系
由图4可知,饼皮含水率在4%~12%时,饼皮的有效扩散系数为1×10-12~2.5×10-11m2/s;饼皮的扩散系数随含水率的增大呈先增加后下降趋势,主要是由于初期含水率低,饼皮内部结构孔隙会急剧吸水,导致水分扩散系数急剧增加,后阶段由于含水率的增加导致饼皮内部结构发生改变,水分的增加会降低饼皮的孔隙率,水分扩散由气态扩散转化为液态扩散,故扩散速率会降低[14]。
2.3 米威化饼干二组分间水分扩散模型验证
通过Fick第二定律结合各组分初始条件、边界条件及等温吸湿模型求得各组分间水分扩散的含水率与时间变化的关系并与试验数据进行比较。试验过程中仅对含水率边界为0.12 g/g前的理论模型部分进行验证。
分析得出,含水率介于0.02~0.12 g/g时,试验数据和理论模型的吻合度高,相关系数R2=0.978 5,具有较高的可靠性,表明该理论模型能很好地反映米威化饼干中饼皮的水分扩散。通过该模型的建立可以为米威化饼干的包装材料选择及防潮保质、货架期的预测提供指导。
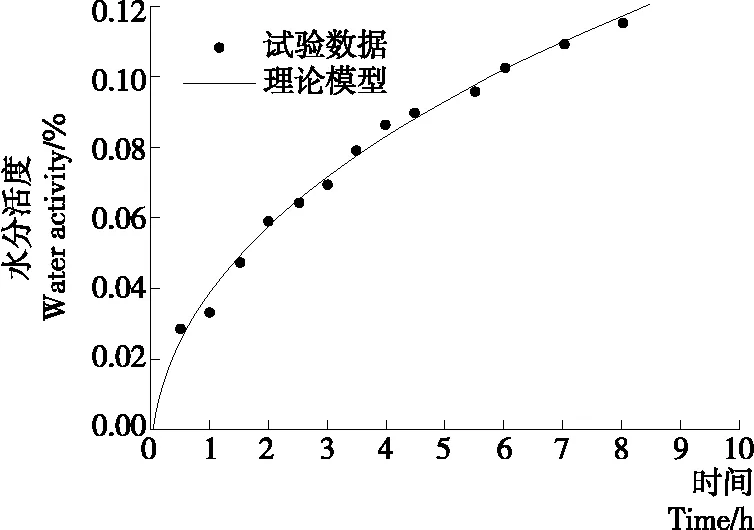
图5 饼皮水分吸附动力学试验数据和数值解模型比较
Figure 5 Comparison between the experimental and model-calculated values of moisture content in crust
3 结论
在非渗透条件下通过结合米威化饼干各组分的等温吸湿模型,利用Matlab求解Fick第二定律的偏微分方程得出饼皮含水率和时间的数值解模型;并采用米威化饼干中的馅料及饼皮进行水分吸附动力学试验验证。结果表明,含水率介于0.02~0.12 g/g时,理论模型与试验数据吻合性高,证明该方法对米威化饼皮水分扩散系数模型的预测具有较高的可靠性。文章仅考虑非渗透条件下水分在组分间的扩散,下一步将研究渗透包装条件下包装外界环境中水分扩散到食品中,为多组分食品防潮包装货架期的预测提供依据。
