考虑加筋体三维变形的桩承式路堤沉降计算方法

2019-10-15崔晓艳王康宇

天津大学学报(自然科学与工程技术版) 2019年12期

庄妍，崔晓艳，王康宇

(1. 东南大学土木与交通学院混凝土及预应力混凝土结构教育部重点实验室，南京 210096；2. 浙江工业大学建筑工程学院，杭州 310023)

加筋体材料是一种新型的岩土工程材料，随着在公路、铁路、水利等工程中的成功应用，加筋体材料目前已经渗透到土木工程的各个领域，在国家基本建设中发挥着重要的作用[1].加筋体在挡土墙中的使用，成功取代了传统的重力式挡土墙，筋材通过与土体之间的相互作用，从而起到限制了土体的位移、保证土体结构稳定的作用.相比之下，加筋挡土墙省时又经济[2].加筋体与桩相结合可以有效地加固软土地基上修建的路堤，能加强应力从路堤填土到桩帽之间的荷载传递，从而减小了路堤表面的不均匀沉降[3-4].但目前对加筋机理的研究还落后于工程实践，加筋体在工程实际中的性状还需要进一步研究.

Giroud等[5-6]对土工格栅的在加筋路堤中的作用进行了一系列研究，提出了张拉薄膜理论，认为土工格栅等加筋材料能促进路堤荷载向桩上传递.赵明华等[7]以单桩有效影响范围内的路堤与复合地基为分析对象，引入大挠度环形薄板考虑加筋垫层的“柔性筏板效应”与“拉膜效应”.Abusharar等[8]对加筋体进行受力分析，考虑加筋体上下表面上作用的剪应力，结合几何尺寸与加筋体变形的关系，建立了加筋体拉力与加筋体变形的函数关系，通过水平与竖直方向上力的平衡方程求解出加筋体的变形.但目前大多方法均认为加筋体的变形为二次抛物线[8-10]，这与桩承式路堤中加筋体的三维变形特点不相符[11-12].因此，有必要对加筋体在工程实际中的变形与受力性状做进一步研究.

加筋体在桩承式路堤中的工作性状，需要结合路堤中的土拱效应与软土的承载作用进行分析.国内外学者提出了不同的土拱模型和计算方法：1943年，Terzaghi通过 Trapdoor试验[13]分析了土拱应力分布特点，得出了土拱效应的存在条件.1987年，Guido等[14]在室内试验的基础上，提出了带有经验性质的理论，采用楔形拱假设，认为土拱的形状为正四棱锥.1988年，Hewlett等[15]提出了基于试验的理论模型，土拱的形状认为是半圆形的具有均匀厚度的拱，研究发现土拱的破坏发生在土拱的拱顶和拱角处，并据此求解出桩土应力比，但在研究中没有考虑加筋体对土拱效应的影响，并且没有考虑软土的承载作用力.英国规范 BS8006[16]基于 Marston的方法对正方形布桩时土拱效应进行了分析.其假设桩顶以上路堤必须有足够的高度才能形成完整土拱，并将能在路堤中形成完整拱的最小路堤高度称为临界高度[17-19].当路堤的高度大于临界高度时，加筋体中的拉力不再随路堤高度的变化而发生改变，这与数值模拟结果并不相符[20].费康等[21]对桩承式路堤中的土拱效应进行了三维模型试验研究，分析了应力折减系数大小和填土中的竖向应力分布特点，但研究中只考虑了软土的沉降，没有考虑软土的承载作用力.

从现有研究中发现，桩承式加筋路堤中的荷载传递特性没有形成一种系统化的研究，且已有的研究中较少能把桩、软土、路堤以及加筋体整体考虑在内进行分析.本文结合加筋体的三维变形特点，推导外界荷载作用时加筋体的三维变形表达式，并据此推导出加筋体的应变、加筋体上作用的竖向应力以及加筋体拉力的求解公式.本文还将加筋体变形三维效应的解析方法应用于桩承式路堤中，从而推求桩承式路堤中考虑土拱效应、加筋体作用以及软土承载作用的简化计算方法.并将结合具体工程实例，从而验证该简化计算方法的正确性.

1 加筋体变形三维效应

1.1 加筋体的三维变形表达式

在目前的研究中，为简化分析，加筋体的变形假设为二次抛物线[8-10]，这与加筋体三维变形的特点不相符.根据 Jones等[11]、Zhuang等[12]研究结果可知，在桩的支撑作用下，加筋体受外力荷载作用时，加筋体的变形形状近似于椭圆抛物面(如图1所示).

图1 椭圆抛物面示意Fig.1 Schematic of the elliptic paraboloid

因此加筋体的三维变形形状可以假设为椭圆抛物面，其表达式为

式中m、n、c为未知参数，其大小与桩间距、桩帽尺寸以及加筋体的最大竖向变形有关.

为求解加筋体的三维变形方程，建立空间直角坐标系，如图 2所示.其中，2桩对角线的中心点为原点O，原点O与桩中心的连线为x轴，垂直于x轴并通过相邻桩中心点的射线为y轴，垂直于Oxy所在平面且过坐标原点的射线为z轴.

图2 空间直角坐标系的建立Fig.2 Establishment of a rectangular coordinate system in space

相邻2桩中心点之间的距离用s来表示，桩帽的边长用a来表示(如图2所示).在4桩的中心O点处，加筋体发生最大竖向变形δmax，可知点(0，0，-δmax)在加筋体变形的曲面上.加筋体在桩帽边缘处的竖向变形为 0，说明点均在加筋体变形的曲面上，将以上 3点代入式(1)可得

因此，加筋体的三维变形方程为

1.2 加筋体应变

在Oxz平面上，加筋体的变形曲线方程为

则

对式(6)进行积分，可得变形后加筋体的长度l′为

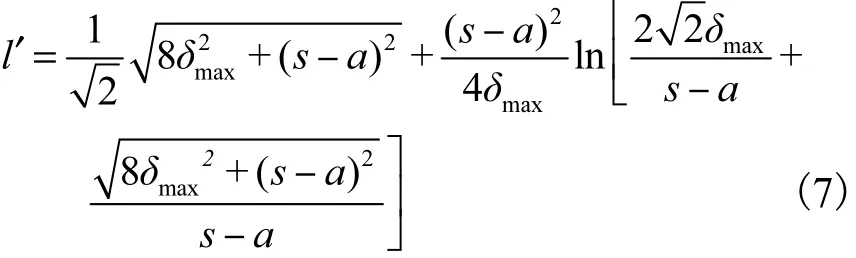
根据定义，可以计算出加筋体的应变为

1.3 加筋体上作用的竖向应力

根据英国加筋土及加筋填土规范 BS8006[16]可知，加筋体所受的拉力T计算式为

式中：WT为作用在加筋体上的竖向荷载；ε为加筋体的应变；a为桩帽边长，对于圆桩需计算其等效边长aeq，且有

式中D为桩的直径.

加筋体上作用的荷载WT的表达式为

式中σg为作用在加筋体上的竖向应力.

将式(11)代入式(9)可得

式中kg为加筋体的抗拉刚度.

由于1/6ε远大于1，式(12)可以近似表示为

因此，可知作用在加筋体上的竖向应力σg为

将式(8)代入式(14)，即可求出加筋体上作用的竖向应力.

2 加筋体变形三维效应在桩承式路堤理论分析中的应用

将加筋体变形的三维效应应用于桩承式路堤中，s为桩间距，a为方形桩帽的边长.以推求桩承式路堤中考虑土拱效应、加筋体作用以及软土承载作用的简化计算方法.

2.1 整体竖向平衡方程的建立

取桩承式路堤底部四桩中心处的微单元体进行受力分析(如图3所示)[22]，可得

图3 路堤底部四桩中心微单元体受力分析Fig.3 Stress analysis of the elements at the centerline of piles

化简式(15)可得

式中：sσ为作用在软土表面上的竖向应力；σG为土拱效应作用下，作用在路堤底部软土中心位置处的竖向应力；sσ与σG的计算过程分别如下文所示.

2.2 软土的竖向承载力

考虑软土发生弹性变形，则软土上作用的竖向应力为sσ，其求解公式为

式中：δmax为软土表面的最大沉降，由于加筋体布置在路堤底部，临近软土上方，因此，加筋体的最大竖向变形认为与软土表面的最大沉降相等；k为地基反力系数，对于分层地基，k的计算公式为

式中：hs为软土厚度；E0为多层软土压缩模量的代表值.当软土表面上作用竖向应力σs时，分层地基的沉降δ计算公式为

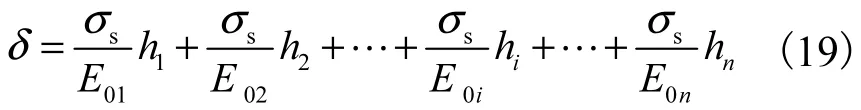
式中：hi为第i层土的厚度；E0i为第i层土的压缩模量，土的压缩模量可以通过弹性模量Ei与泊松比vi换算，即

根据sσ＝E0δ/hs，并结合式(19)，可得

将式(21)代入式(17)，可以求解出软土上作用的竖向应力.

2.3 土拱效应作用下路堤底部的竖向应力

2.3.1 桩为正方形布置

基于不均匀拱厚，Zhuang等[23]对 Hewlett等[15]土拱理论中内外拱高度进行了修正，得到结果如下.

当土拱破坏发生在拱顶时，σG的表达式为

式中：γ为路堤填料的重度；hout为土拱外拱的高度；hin为土拱内拱的高度，表达式分别为

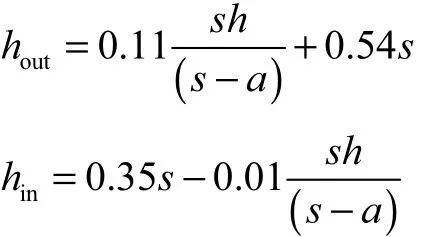
当土拱破坏发生在桩帽处时，σG的表达式为

其中

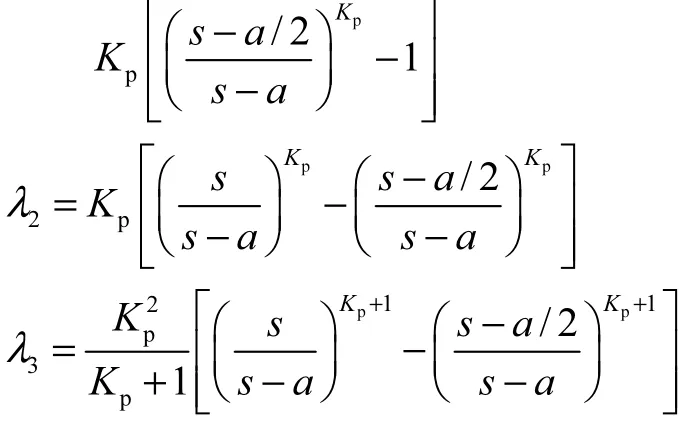
2.3.2 桩为梅花形布置

桩为梅花形布置的平面图如图 4所示，其中，桩间距为s，桩帽边长为a，分析单元如图4中阴影部分所示.建立空间直角坐标系，其中，AC与BD的交点为原点O，AC所在的射线为x轴，BD所在的射线为y轴，垂直于 Oxy所在平面且过坐标原点的射线为 z轴.桩为梅花形布置时，假设ABCD所在区域上作用1个空间土拱与4个平面土拱(如图5所示)，由图5可知每个桩帽上作用4个拱脚.

图4 方桩为梅花形布置时土拱形状Fig.4 Shape of the arching for the piles arranged in a triangular pattern

1) 土拱破坏发生在拱顶

取空间土拱拱顶的微单元体进行受力分析得

径向应力rσ与切向应力θσ之间的关系为θσ＝Kpσr则式(24)的通解为

式中c为积分常数.

假设在梅花形布置情况下，外拱土拱的高度为OO′(如图 4所示)，则边界条件为：当时则方程(25)的解为

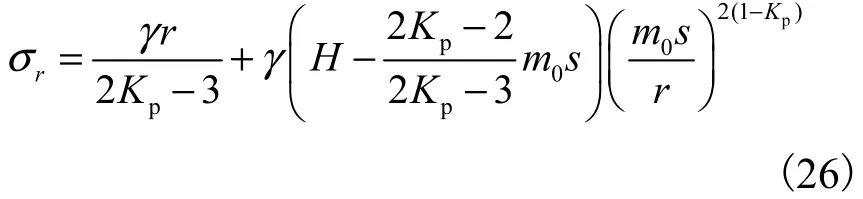
则作用在内拱位置处(r＝m0s-a/2)的竖向应力σin可表示为

则作用在路堤底部软土中心的应力Gσ为

2) 土拱破坏发生在桩帽

由前文假设可知，图4所示的ABCD区域中，相邻2桩帽上作用的为平面土拱，4桩中心作用的为三维土拱.土拱在桩帽上的作用区域如图 5所示，为了方便计算作用在桩帽上的荷载，采用与正方形桩帽面积a2相同的圆来近似代替，可知圆的半径约为1.12a.从图 5中可以看出，每个桩帽上作用 6个拱脚，每个拱脚上作用的荷载为cP′，则每个桩帽上作用的竖向荷载Pc＝6cP′.

图5 桩帽上作用土拱区域Fig.5 Area of the arching acting on the pile cap

根据桩帽上作用的是平面土拱，取桩帽边缘处微单元进行受力分析，该微单元的应力平衡方程为

根据边界条件，当r＝s/2-0.56a时，rσ＝KpσG，可计算出该微分方程的解为

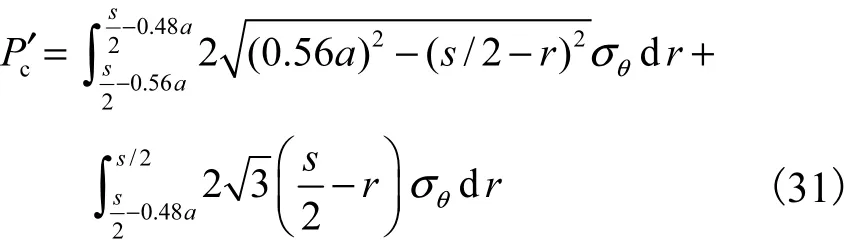
根据θσ＝Kpσr，并将式(30)代入式(31)，可知的表达式为

则作用在桩帽上的荷载Pc为

根据图 6可知，在ABCD区域由一个完整的桩帽与所在区域的路堤填料组成，根据竖直方向上整体力的平衡方程可得

将式(32)、(33)代入式(34)，可以计算出作用在路堤底部软土中心的竖向应力σG的表达式.

将路堤底部软土中心的竖向应力σG、加筋体上的竖向应力σg以及软土上作用的竖向应力σs代入式(16)，即可求解出未知量σmax，则桩承式路堤中加筋体上所作用的竖向应力、加筋体中的拉力、软土表面处所作用的竖向应力均可求解，进而桩承式加筋路堤中软土中心上方至路堤表面的竖向应力分布规律即可获得.

图6 桩帽上荷载的计算Fig.6 Calculation of the load acting on the pile cap

3 解析方法的验证

将桩承式路堤中，考虑加筋体变形三维效应的理论分析方法应用于以下两个工程实例中，以验证该理论分析方法的正确性，该理论分析方法的计算流程如图7所示.

图7 计算流程Fig.7 Flow chart of calculation

3.1 上海高速公路实例

上海某高速公路采用 PCC桩承式路堤[24]，路堤高为5.6m，重度为18.5kN/m3.PCC桩为方形布置，桩间距为 3.0m，桩帽为圆形，直径为 1.0m，单层加筋体铺设在桩帽的顶端，加筋体的刚度为1.18MN/m.软土分为 5层，总厚度为 25m，其参数如表 1所示，其中每层土的压缩模量E0i用式(20)计算获得.

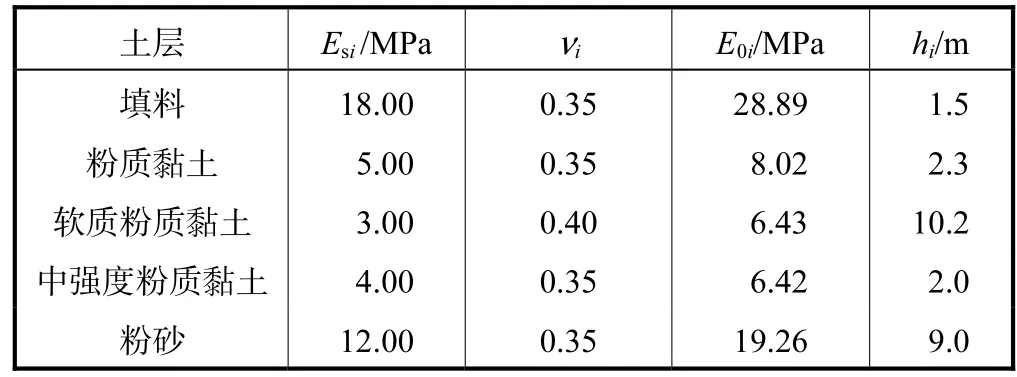
表1 上海高速公路软土基本参数Tab.1Summary of subsoil properties of the Shanghai highway

采用本文提出的理论分析方法计算不同桩间距下，该高速公路路段软土表面的最大沉降，如图 8所示.从图 8中可以看出：随着桩间距的增加，软土表面的最大沉降基本呈现线性增加的趋势，当桩间距由2.0m 增大到 3.5m 时(桩间距增大 75%)，软土表面的最大沉降增大约86%.当桩间距为3m时，理论方法计算出软土表面的最大沉降约为70mm，现场实测值为 87mm，误差为 19.5%，说明了该理论分析方法的正确性.

图8 本文方法与现场监测结果对比(上海高速公路)Fig.8 Comparison between the results from the proposed analytical method and on-site measurements(Shanghai highway)

3.2 大型室外试验

该室外试验路段采用桩承式路堤[25]，路堤的高度为 1.08m，路堤的重度为 18.0kN/m3.其中，桩为方形布置，桩间距为 2.5m，桩帽为方形，边长为0.8m，单层加筋体铺设在桩帽的顶端，加筋体的刚度为 1.3MN/m.软土分为两层，总厚度为 12.5m，其参数如表2所示.

表2 室外试验软土基本参数Tab.2 Properties of soft layers for the outdoor experiment

图9为理论分析方法与现场监测结果的对比，可以看出：随着桩间距的增加，软土表面的最大沉降逐渐增大，当桩间距由2.0m增大到3.5m时(桩间距增大 75%)，软土表面的最大沉降增大约 95%.当桩间距为 2.5m时，理论方法计算出软土表面的最大沉降约为 113mm，现场实测值为 100mm，误差为13.0%，验证了该理论分析方法的正确性.