一种设备状态监测的贝叶斯正则化BP神经网络

2019-10-15孙发友蒙祖强

网络安全技术与应用 2019年10期

◆孙发友蒙祖强

◆孙发友蒙祖强

（广西大学计算机与电子信息学院广西 530004）

设备全过程监测是有效消除设备隐患的重要环节，依据设备运行数据快速、准确、可靠的创建运行状态模型是建立故障早期预警的关键。以火电厂为例，由于火电厂现场生产环境复杂，正常状态设备会产生异常数据，本文首先将采用两倍差法进行数据清洗剔除异常数据，其次利用因子分析算法提取综合指标，最后基于贝叶斯正则化BP神经网络建立预测状态模型。将模型输出预测值与实测值进行计算产生设备状态信息。实验结果表明，预测模型输出值与实际状态值匹配度超过90%，已经达到实际生产环境要求，具有推广价值。

数据清洗；综合指标；贝叶斯正则化；BP神经网络；预测模型

现场运行设备的状态是一个实时动态变化的过程，通过在整个电厂建立主要生产设备运行状态的早期故障监测预警，构建起厂级的数据挖掘和设备健康管理系统，从而大大降低设备潜在的事故发生概率，缩短关键设备的非计划停机时间，提高设备的可靠性和可利用率[1]，降低设备维护运行成本。为此，需要解决一下问题：

（1）设计从设备日常运行的海量数据中自动过滤异常数据的算法。

（2）每个设备实时监测了多方面的特征参数，基于筛选过的数据，设计提取代表设备状态的综合指标的算法，从而优化监测数据处理的维度和监测成本。

（3）建立设备状态预测模型，能依据现有的设备状态值输出预测设备状态值。利用预测值与实际值的相似度产生设备状态信息。

设备状态数据为结构化数据，并且其数据分布为非正态分布。为了达到实验目标，采用基于贝叶斯正则化BP神经网络模型，加快数据收敛，同时该状态预测模型需要能够进行数据的自我学习，即依据自身已有的数据预测未来的数据。实验表明该模型具有拟合曲线光滑，较好的数据泛化能力，具备推广应用前景。

本文使用MATLAB进行贝叶斯正则化BP神经网络的模拟。

1 相关原理与算法

1.1 剔除异常数据-两倍差算法

1.1.1 概念与原理

通过实践发现设备大部分数据不符合正态分布[2]，故采用两倍标准差法进行的数据清洗，形成设备健康数据库，保证采集的数据符合设备监测的需要。

选取设备正常运行的一段时间内测点的特征数据值，计算该组数据的平均值`、方差。对于区间[`-，`+]内的数据予以保留，超出范围的属于异常数据，予以剔除。相关公式为：

平均值：

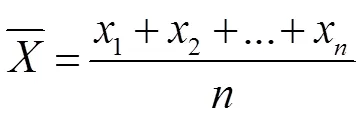
方差：

假设有测点{1，2，…，P}，第条纪录为{1k，2k，…，X}。现在假设共有条数据。则第条纪录予以保留必须满足如下条件：

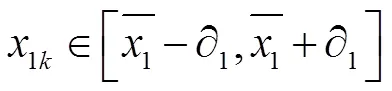
两倍差算法是在实验开始时，对原始异常数据的过滤。

1.1.2 算法描述

算法名称：两倍差算法输入：X 输出：二维数组Y 伪代码：BeginS1：[1…n]，[1…n]；/*定义平均值矩阵，方差矩阵*/S2：for var i←1 to 矩阵X的列数 dosum←0；/*定义列求和变量sum */for var j←1 to矩阵X的行数 dosum←sum+矩阵X的i行j列数据；End[i] ←sum/矩阵X的行数；/*参照公式（1）求第i列平均值*/sum←0； /*sum变量清零，为求方差做初始化 */for var j←1 to矩阵X的行数 dosum←sum+(矩阵X的i行j列数据-[i])2End[i] ←sum/（矩阵X的行数-1）；/* 参照公式（2）求第i列方差*/Endfor var i←1 to 矩阵X行数 dofor var j←1 to 矩阵X列数 domin←[j]-[j]， max←[j]+[j]； /*参照公式（3）求第i列数据范围*/if（矩阵X的i行j列数据 max） then中断；end ifif（j=n） then /*参照公式（3）表明第i行数据都在指定范围内*/矩阵Y中添加矩阵X的第i行。end ifendendEnd.

1.2 样本综合得分-因子分析法

因子分析以较少的几个因子反映原资料的大部分信息[3]。利用重新组合后的相互无关的综合因子来代原来指标（综合因子必须满足“累计方差贡献率“>80%），以降低数据处理的维度和监测成本，形成降维健康样本集。通过因子分析法计算得到因子综合得分，为神经网络提供数据源。

1.2.1 因子分析的数学模型

1.2.2 因子分析适用性检验

适应性分析是检验数据适合神经网络训练的基础，将两倍差过滤的数据进行检验后，再进行因子分析。适用性检验采用以下方法：

（1）巴特莱特球体检验。

在spss中的因素分析时有关于bartlet 球形检验的选项，如果sig值小于0.05，则数据呈球形分布[6]。

（2）KMO 检验.

KMO取值范围为[0，1]。KMO值越接近于1，意味着变量间的相关性越强，原有变量越适合作因子分析。kmo度量标准：0.9以上表示非常适合；0.8表示适合；0.7表示一般；0.6表示不太适合；0.5以下表示极不适合[7]。

1.2.3 因子分析步骤

（1）数据归一化。

归一化是将数据按比例缩放，使之在特定小区间范围，消除数据的单位影响，将其转换为单位无关的纯数值。本次实验中根据数据特点，将数据统一映射到[-1，1]区间上。

（2）矩阵标准化。

（3）求解矩阵特征值、特征向量。

（4）求得方差贡献率（含累计）。

特征值>1的原则，确定前个提取因子的累计贡献率不低于80%，则前个因子来代表评价。

（5）利用方差最大方差法旋转获得因子载荷矩阵，建立便于解释意义的因子模型。

（6）通过回归算法获得因子得分系数，从而获得因子得分表达式。

假设数据归一后的矩阵为：

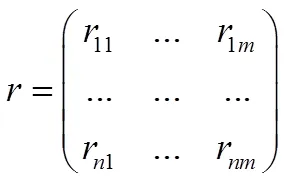
有个综合因子，并且因子得分系数矩阵为：

则第行数据（r1，…，r）的个得分因子计算公式为：

…..

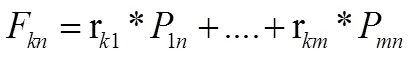
（7）计算因子综合得分：以各因子的方差贡献率为权，各因子的线性组合得到各综合评价指标函数[8]。

通过公式（8）获得因子综合得分，为神经网络提供数据源。

1.2.4 算法描述

算法名称：样本综合得分输入：过滤后的数据矩阵Y 输出：综合得分数数组S=[] 伪代码：BeginS1： [sig，KMO] ←对Y进行巴特莱特球体检验、KMO检验S2：if（sig>0.05）or（KMO<0.7）then /*详见1.2.2节*/S3：结束；S4：end if/*步骤S5~S21的描述，详见1.2.3节*/S5： r←矩阵Y归一化； /*参照公式（5）*/S6： vec[1..p]←提取矩阵r的特征向量；S7： val[1..p] ←提取矩阵r的特征值；S8： fai[1..p]←从val[1..p]获取方差贡献率；S9： psai[1..p]←从val[1..p]获取累计方差贡献率；S10： num←0； /*公因子个数*/S11： for var i←1 to psai.length do /*求公因子个数*/S12： if（psai[i]>0.85） thenS13： num←i；S14：中断；S15：end ifS16： endS17： A←根据vec[1..p]获取荷载矩阵；S18： B←根据A获得旋转荷载矩阵；S19： P←根据B与r计算出得分数据矩阵/*参照公式（6）*/S20： F←P*Y /*参照公式（7）计算每行因子得分值，F为矩阵*/S21： S[1..n] ←矩阵F* fai[1..p]；/*参照公式（8）计算因子综合得分*/End

1.3 贝叶斯正则化方法的BP神经网络

1.3.1 基本BP神经网络

BP神经网络是一种多层的前馈神经网络，特点是利用信号正向传播，而通过逆向传播调整连接权重和网络节点阀值[8]。通过多次训练是的预测模型的输出值逼近期望值。

（1）BP神经网络学习过程

详细流程可以描述如图1。

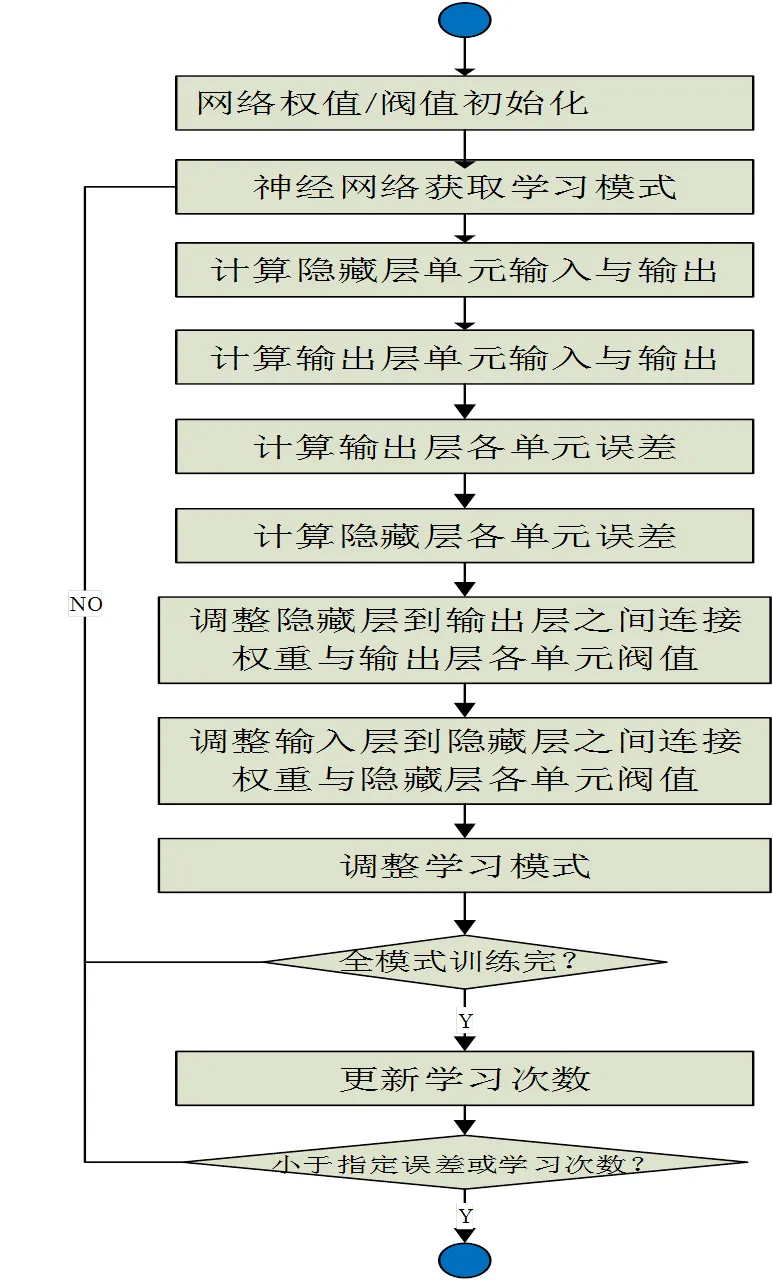
图1 BP学习流程图

（2）隐层神经元数选取

在BP神经网络中，输入层和输出层的节点个数都是确定的，而隐含层节点个数不确定。隐含层节点需要适当，节点少网络处理能力变弱，节点过多则使网络结构变复杂且增加处理复杂度。隐层结点数的选择问题未有统一结论实践证明，大部分情况可一采用公式：

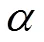
1.3.2 贝叶斯正则化的BP神经网络

BP神经网络对于训练的数据能很好拟合，但是训练集外的数据拟合就很差强人意，即网络存在过拟合现象，泛化能力较弱。

网络结构和样本训练的策略是决定BP神经网络的关键要素。因此可以从这两个方面入手，提高网络泛化能力。训练策略包括在训练样本中加入噪声、提前停止法等方法；网络结构优化方法则包含正则化法、数据集扩增、修剪法等[9]。

实验表明提高BP神经网络泛化能力有效途径是正则化。贝叶斯正则化是在平方误差性能函数的基础上，加入惩罚函数，实现对性能函数的修正，提高网络泛化能力。平方误差函数的公式为：

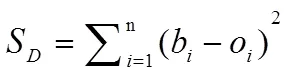
此时网络所有权值均方误差：

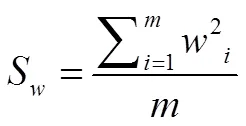
在贝叶斯正则化方法中引入了惩罚函数后，修正后的性能函数变为：

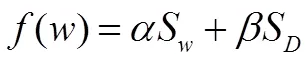
1.3.3 贝叶斯正则化方法

贝叶斯正则化的目标是得到最好性能、最小参数化的神经网络，从而解决拟合的问题[10]。假设训练数据集中的噪声和向量（包含网络所有权值和偏置值的向量）服从高斯分布，则权值函数密度与修正后的性能函数为：

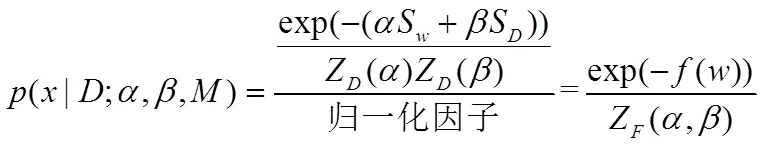
表达式中参数的含义如下：

（4）：代表了所选取的网络结构。

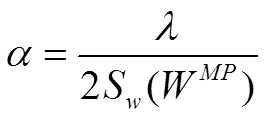
公式中参数含义如下：

（2）为神网络参数总个数

通过高斯-牛顿法近似计算矩阵，该算法能有效地提高BP神经网络的泛化能力。

1.3.4 算法描述

本次实验隐藏层神经单元个数计算采用公式（9）。

本次实验中采用matlab作为工具，BP神经网络函数选用如表1。

表1 BP神经网络选用函数表

训练函数采用trainbr，表明采用贝叶斯正则化算法的BP神经网络，如表2。

表2 BP网络训练参数配置表

1.4 BP神经网络预测模型的选取

1.4.1 概念与原理

BP神经网络做预测有两种形式：

（1）依据已有数据预测未来的数据。即已经知道前-1个值，预测第个值。

输入数据集与预测结果集的个数为：

=-（14）

输入数据集：

预测结果集:

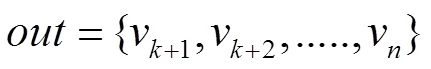
（2）依据已知的属性，预测未知的属性。即某对象有个属性，已知-1个属性值，预测第个属性的值。

火电厂设备状态检测测点数据矩阵为：

1.4.2 算法描述

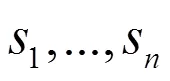
按照1.4节采用了“依据已有数据预测未来的数据”的预测模型方案。针对该方案，本次实验采用每5个数据预测1个结果，即如果有个数据则有-5组预测数据和结果。

算法名称：提取训练数据输入：数据集矩阵S=[]，步长step=5 输出：in={ n-5组预测数据}与 out={ n-5组预测结果} 伪代码：Begin/*返回训练输入、输出数据集*/function [in，out]=GetTrainData（S，step）len← S.length -step； /*参照公式（14） */t_in[1..len]，t_out[1..len]；for var i←1 to len doif（i+step>len） /*超出训练数据个数退出*/终止循环；end if[c_in，c_out]=in_out（S，i，step）；t_in[i]←t_in[i]+c_in；t_out[i]←t_out[i]+c_out；endin←t_in； /*参照公式（15）输入数据集 */out←t_out； /*参照公式（16）输出数据集*/end function/*参照公式（15），（16）的数据结构，返回一组输入数据、一个输出数据*/function [m_in，m_out]=getData（arrary，start ，step）stop=start+step-1；res[1..step]；for var i←start to stop dores[i]←arrary[i]；endm_in←res； /*输入数据集*/m_out←arrary[stop+1]； /*输出数据*/end functionend

测试数据集获取算法与此雷同，不再描述。

1.5 火电厂状态预警方法

设计一个设备状态得分算法，合理表示设备状态。通过不同状态做出提示。假设实时数据样本综合得分值为，神经网络产生的预测值为。

（1）实时数据样本综合得分由因子分析算法计算得出。

（2）预测值为由训练后的神经网络产生。

通过实时值与预测值之间的相似度比较结果，可以划定设备状态，包括正常、注意、严重、异常状态。相似度计算公式为：

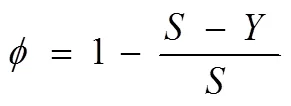
表3 设备状态预警表

2 实验分析

本文实验数据的均来自电厂的原始数据，由于电厂设备众多，本次实验选择了气泵前置泵作为研究对象，该设备有7个测点，由于数据量巨大，本文仅列出部分测点数据（表4）：

表4 汽泵前置泵测点数据值

首先，将原始数据通过两倍差算法进行过滤（图2），筛选过后的数据整体在某一个范围波动，完成过滤异常数据的目的。

其次，过滤后的数据，通过因子分析提取公共因子（图3），由于前2个主成分其累计方差贡献率为92.231%，故存在2个公共因子。通过因子得分系数与旋转方差，计算得到样本综合得分数据集（表5），为神经网络提供数据源。

最后，基于样本综合得分数据集，通过贝叶斯正则化BP神经网络建立预测模型。同时针对预测模型进行测试，测试结果如图4。该神经网络参数设置输入数据节点=5，隐藏层节点=7，输出节点=1。为了对比效果，将同样的数据集采用基本梯度下降法BP神经网络建立预测模型，测试效果如图5。

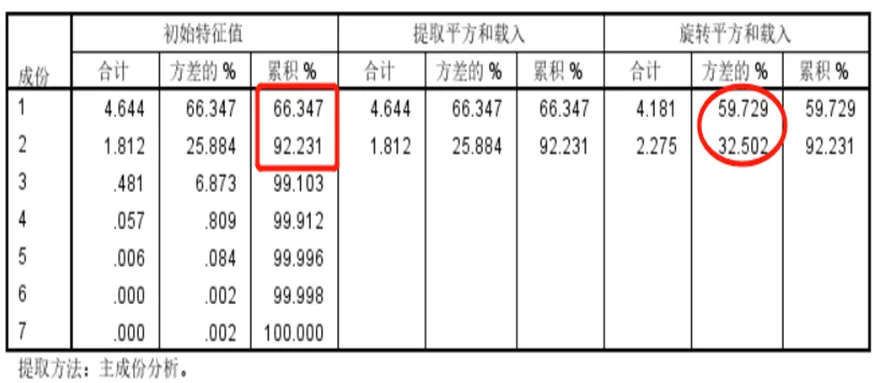
图3 解释的总方差

表5 成分得分系数矩阵

图4 BP神经网络实际值(红)与预测值(蓝)曲线

图5 梯度下降法实际值(红)与预测值(蓝)曲线

从实验中可以看出，通过两倍差法过滤后的曲线比较平滑，为建立预测模型提供数据基础。通过因子分析找到影响设备状态的关键因素，有效降低了数据处理的复杂度，并获得样本综合得分的数据集。最后，基于贝叶斯正则化BP神经网络建立的预测模型，其拟合效果非常好，预测模型输出值与实际值高度相似，达到生产环境的实际要求。基于此，可以通过预测模型输出值与实际值之间的相似度及时提供设备可靠的预警信息。