基于卷积自编码器的图像压缩

(成都理工大学 四川 成都 610059)

一、介绍

自动编码器有潜力解决日益增长的有损压缩算法的需求。根据不同的情况，需要不同计算复杂度的编码器和解码器。开发一种新的编解码器可能需要数年时间，但基于神经网络的更通用的压缩框架可能能够更快地适应这些不断变化的任务和环境。不幸的是，有损压缩本质上是一个不可微的问题。我们的目标是直接优化自动编码器产生的速率失真权衡。通过提出了一种简单而有效的方法来处理基于四舍五入的量化的不可微性，并逼近生成系数编码的不可微代价。

通过使用这种方法，我们可以获得与jpeg2000相似或更好的性能。然而，与jpeg2000不同的是，我们的框架可以针对特定的内容(例如缩略图或非自然图像)、任意指标进行优化，并且易于推广到其他方面。

二、压缩自编码器

定义一个压缩自编码器(CAE)有三个组件:编码器f，解码器g和概率模型Q，

f:N→M,g:M→N,Q:M→[0,1].

(1)

由Q定义的离散概率分布用于根据比特数的频率将比特数赋给表示，即熵编码。这三个组件可能都有参数，我们的目标是优化使用少量比特和具有较小失真之间的权衡，

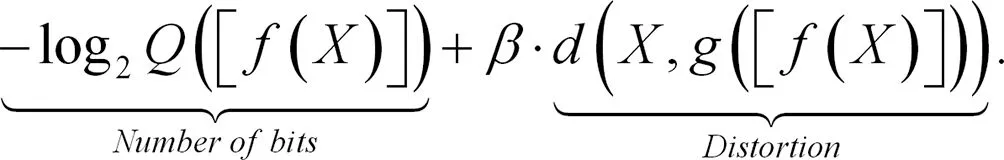
(2)

这里,β控制的权衡,方括号表示量化舍入到最接近的整数,和d措施引入失真编码和解码。编码器的量化输出是用于表示图像并无损存储的代码。遗憾的是，我们不能使用基于梯度的技术直接优化方程(2)，因为Q和[·]是不可微的。下面两部分提出了解决这个问题的方法。

(一)量化与可微替代。我们建议用光滑近似r的导数代替它在反向传播的后向传递过程中的导数(Rumelhart等人，1986)，即有效地定义导数为

(3)

重要的是，并没有完全用光滑的近似来代替舍入函数，而只是用它的导数来代替，这意味着在前向传递中仍然像往常一样进行量化。从经验上看，发现等式r(y)=y和更复杂的选择一样有效。这使得该操作易于实现，因为我们只需将梯度传递给编码器，而无需修改解码器。注意，如果d是可微的，那么相对于解码器s参数的梯度可以不用近似计算。与相关方法相比，我们的方法的优点是不改变解码器的梯度，因为前向传递保持不变。

接下来，将讨论其他作者提出的替代方法。受抖动理论联系的启发，Ballé等(2016)提出用加性均匀噪声代替量化，

[f(X)]≈f(X)+u.

(4)

另一方面，Toderici等人(2016a)使用了随机形式的二值化(Williams,1992)。将这一思想推广到整数，我们定义了以下随机四舍五入操作:

{y}≈⎣y」+ε,ε∈{0,1},P(ε=1)=y-⎣y」,

(5)

其中⎣.」为楼层操作员。在向后传递过程中，导数被期望的导数代替，

(6)

(二)熵率估计。由于Q是一个离散函数，不能对它的参数求导，我们先用概率密度Q表示模型s分布q，从而将不可微比特数上界，

(7)

上界由：

(8)

其中第二步是从Jensen ‘s不等式推导而来(参见Theis等人，2016)。上界的无偏估计是通过从单位立方体中采样u得到的[-.5,.5[M。如果我们使用可微密度，这个估计在z上是可微的，因此可以用来训练编码器。

(三)可变比特率。在实践中，我们常常希望对所使用的比特数进行精确的控制。实现这一点的一种方法是训练一个自动编码器，以适应不同的速率失真权衡。但这将要求我们培训和存储大量潜在的模型。为了降低这些成本，我们通过引入比例参数λ∈M，对一个预先训练的不同速率的自动编码器进行了微调，

-log2q([f(x)°λ]+u)+β·d(x,g([f(x)°λ]/λ)).

(9)

这里，°表示点乘和除法也按点乘执行。为了减少可训练比例尺的数量，它们可以进一步跨维度共享。例如，当f和g是卷积的时候，我们共享跨空间维度的尺度参数，但不共享跨通道的尺度参数。

三、相关工作

与这样的做法最密切相关的是Ballé等人(2016)的工作。主要的区别在于处理量化和熵率估计的方式。Ballé等人(2016)所使用的变换由单一线性层和一种对比度增益控制形式组成，而本文的框架依赖于更标准的深度卷积神经网络。

Toderici等(2016a)提出使用递归神经网络(RNNs)进行压缩。与本文工作中的熵编码不同，网络试图将给定比特数的失真最小化。图像以迭代方式编码，并在每个步骤中执行解码，以便能够在下一次迭代中考虑残差。这种设计的一个优点是它允许图像的渐进编码。缺点是它的压缩比本文的方法耗费更多的时间，因为本文使用高效的卷积神经网络，并且在编码阶段不需要解码。

Gregor等人(2016)探索了使用变分自编码器与循环编码器和解码器对小图像进行压缩。这种类型的自动编码器被训练成最大化对数可能性的下界，或者等价地最小化

(10)

其中p(y|x)为编码器，q(x|y)为解码器。而Gregor等人(2016)使用编码器的高斯分布,我们可以联系他们的工作方法Ballé等人(2016)通过假设它是制服,p(y|x)=f(x)+u。果我们还假设固定方差的高斯可能性,q(x|y)=Ν(x|g(y),σ2Ι),目标函数可以写

(11)

这里C是一个常数，它包含编码器的负熵和高斯似然的归一化常数。注意,这个方程是相同的率失真的权衡与β=σ-2/2和量化取代添加剂均匀噪声。然而，并不是所有的失真都有一个等价的公式作为一个变分自动编码器(Kingma & Welling,2014)。只有当e-d(x,y)在x中可归一化且归一化常数不依赖于y时，这才成立，否则C就不是常数。

四、结论

在未来的工作中，希望探索不同指标下压缩自编码器的优化方法。Bruna 等人(2016)提出了一个很有前景的方向，他使用基于训练的用于图像分类的神经网络的度量获得了有趣的超分辨率结果。Gatys等人(2016)使用了类似的表示方法，在感知意义风格转移方面实现了突破。感知度量的另一种选择可能是使用生成的对抗网络(GANs;Goodfellow等，2014)。基于Bruna等人(2016)和Dosovitskiy & Brox等人(2016)的工作，Ledig等人(2016)最近将GANs和基于特征的度量标准结合起来，展示了令人印象深刻的超分辨率结果。