曲线段钢轨焊接接头不平顺对轮轨动力响应的影响研究*
2019-10-14张克平石广田和振兴张小安包能能
张克平 石广田 和振兴 张小安 包能能 石 蕊
(兰州交通大学机电工程学院,730070,兰州//第一作者,硕士研究生)
目前,城市轨道交通正线线路均采用平顺性较好的无缝线路。但无缝线路钢轨间焊接接头是其最薄弱的环节之一[1]。受焊接材料、焊接工艺水平、养护维修等多方面因素的影响,在车轮反复辗压作用下,钢轨焊接接头会发生低塌等病害[2],形成焊接接头不平顺。钢轨焊接接头不平顺会造成巨大的轮轨冲击,影响行车安全性和乘坐舒适性。
针对钢轨焊接接头不平顺对轮轨系统动力响应的影响,国内外学者开展了大量的研究工作。文献[1]建立车辆-轨道耦合动力学模型及有限元模型,分别研究了高速铁路钢轨焊接接头实测不平顺和理论不平顺对轮轨动力响应的影响规律;文献[3]通过建立高速铁路车辆-道床垂向耦合模型及有限元模型,研究了钢轨焊接接头不平顺对车体、轮轨、弹条和轨道板等动力响应的影响规律;文献[4]研究了重载货车通过时,钢轨焊接接头不平顺对轮轨动力响应的影响规律,并将焊接接头不平顺作用下轮轨动力响应的理论计算结果与实测结果进行了对比分析。
本文运用车辆-轨道耦合动力学理论[5],建立了地铁A型车的车辆-轨道空间耦合动力学仿真模型,分别对曲线段两种典型焊接接头不平顺激扰下的城市轨道车辆轮轨动力响应规律展开研究,并对现有《地铁设计规范》规定的钢轨焊接接头不平顺限值进行了验证。
1 模型建立及参数选择
1.1 车辆-轨道耦合模型
由于车辆通过曲线时既有垂向运动又有横向运动,且横向运动规律受轨道超高和行车速度的影响较为显著。因此,本文基于车辆-轨道耦合动力学理论,采用UM(Universal Mechanism)动力学仿真软件,建立车辆-轨道耦合系统动力学模型[5],模型如图1所示。

图1 车辆-轨道空间耦合系统模型
该模型主要由车辆模型、轨道模型及轮轨相互作用关系模型组成[7]。车辆模型选用地铁A型车模型。轨道模型中:轨枕模型选择UM软件默认的柔性钢轨和刚性轨枕;柔性钢轨将左右两股钢轨均视为连续弹性离散点支撑无限长Euler梁;刚性轨枕具有垂向、横向振动及转向运动自由度;钢轨与轨枕,以及轨枕与轨下基础的垂向和横向均通过线性弹簧和阻尼元件连接;相邻的道床支撑单元通过剪切刚度和剪切阻尼连接;模型将道床离散为刚性质量块,使其只有垂向运动自由度;道床块之间由剪切刚度和剪切阻尼原件连接。轮轨相互作用关系是通过轮轨接触来实现两个子模型系统间耦合的;车轮踏面外形选择Chinese LMA,钢轨轨头外形选择T60轨。
相对于在直线段,在曲线段不仅轮轨受力更为复杂,而且相同列车运行速度下由焊接接头激扰造成的轮轨冲击也明显更大。因此,研究曲线路段焊接接头不平顺激扰对轮轨力的影响更具代表性。线路的曲线段模型如图2所示,其中轨道外轨超高设为119 mm。
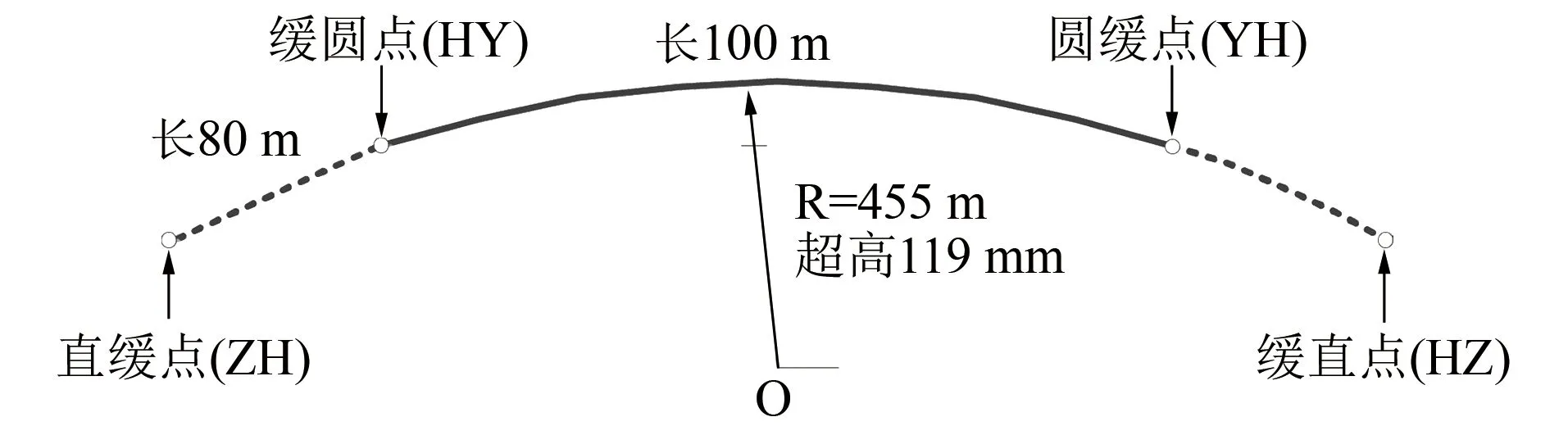
图2 线路的曲线段模型
1.2 钢轨焊接接头不平顺模型
钢轨焊接接头不平顺是城市轨道交通无缝线路的典型不平顺。最常见的钢轨焊接接头不平顺主要有单一余弦型谐波不平顺和叠加型短波不平顺两种[6],其中单一余弦型谐波不平顺又可分为凹型和凸型两种。
由于我国铁路标准对焊接接头不平顺的打磨标准要求按焊接区长度为1 m考虑,所以凹型谐波不平顺和凸型谐波不平顺的数学函数均可用波长为1 m的单一余弦函数式来表示,只是其不平顺方向相反[6]。其函数式如式(1)所示。由于波长较短的凸形焊接接头不平顺在实际铺设及养护维修作业过程中已经被打磨掉,所以本文只考虑凹型谐波不平顺,如图3所示。叠加型短波不平顺模型则为1 m凹型余弦谐波上叠加一更短谐波不平顺,如图4所示,其描述函数见式(2)。
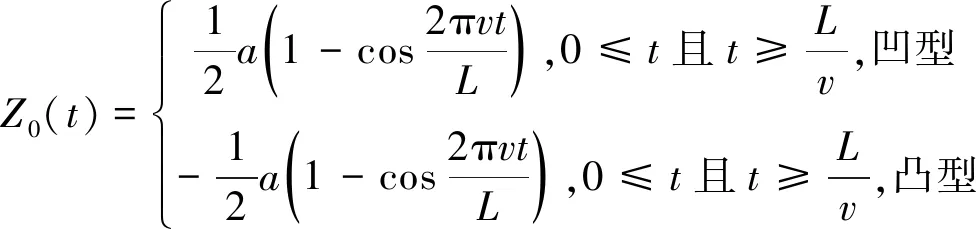
(1)

(2)
式中:
Z0(t)——激扰位移;
a——不平顺波深;
L——不平顺波长;
v——行车速度;
λ——短波不平顺波长;
a1——长波不平顺波深;
a2——短波不平顺波深。
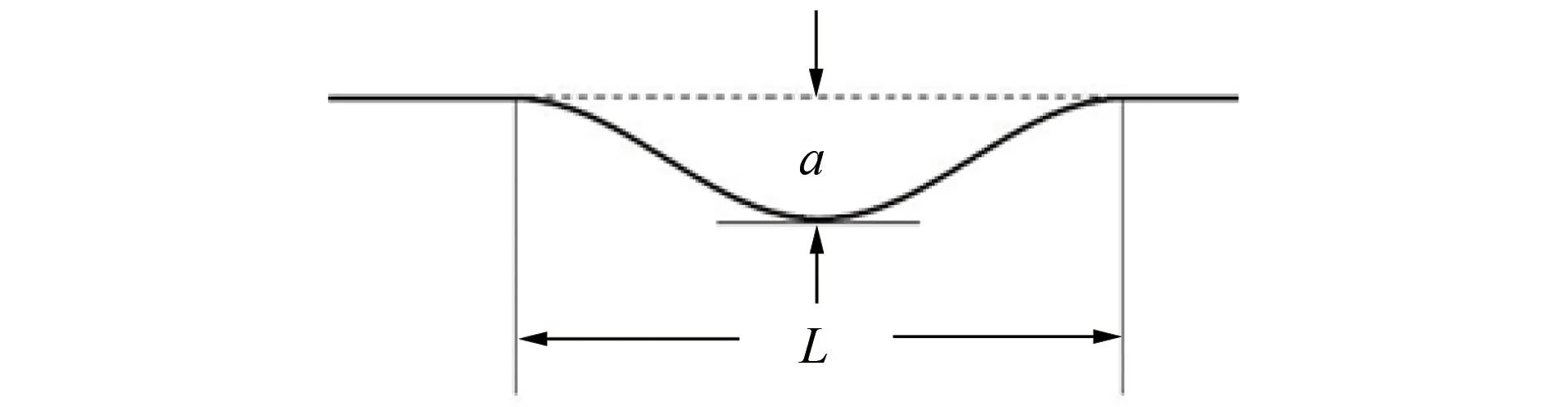
图3 凹型余弦型谐波不平顺

图4 叠加型短波不平顺模型
2 两种不平顺模型对应的动力响应
根据GB 50157—2013《地铁设计规范》7.2.3条规定[9],超高允许值[h]≤120 mm,欠超高允许值[hq]≤61 mm,过超高允许值[hg]≤50 mm,超高顺坡率不大于2%。针对本文所选曲线段119 mm超高值,通过超高计算公式分别确定了三个速度工况,即过超高时的速度为48 km/h,正常速度为68 km/h,欠超高时的速度为81 km/h,分别对曲线段两种典型焊接接头不平顺模型激扰下不平顺波长和波深对轮轨动力响应的影响规律展开研究。
2.1 波长对轮轨动力影响
图5为余弦型焊接接头不平顺激扰下不平顺波长对轮轨动力影响曲线,不平顺波深a0=0.30 mm。由图5可知,当钢轨焊接接头不平顺采用如图3所示的余弦型谐波不平顺时,随着不平顺波长λ0的增大,轮轨垂向力和轮重减载率均呈逐渐减小的趋势。当λ0<0.7 m时,轮轨垂向力变化幅度较大;当λ0为0.7~1.2 m时,轮轨垂向力变化幅度明显减小;当λ0>1.2 m时,轮轨垂向力的变化幅度基本趋于平缓。随着列车运行速度的提高,轮轨垂向力和轮重减载率指标也相应增大;λ0越小,轮轨动力指标受列车运行速度的影响越明显。不同的是,当λ0为0.1~0.7 m时,轮重减载率随速度的变化最为明显,当λ0<0.1 m和λ0>0.7 m时,轮重减载率随速度的变化幅度均趋于平缓。
图6为在叠加型短波不平顺激扰下不平顺短波波长λ1对轮轨动力响应的影响规律曲线,长波波长λ2=1 m,长波波深a1=0.30 mm,短波波深a2=0.10 mm。图6表明,当钢轨焊接接头不平顺采用如图4所示的叠加型短波不平顺时,在相同速度条件下,轮轨垂向力和轮重减载率均随λ1的增大而减小。当λ1大于0.12 m时,轮轨垂向力变化幅度明显减小。随λ2的增大,轮重减载率在整体减小的趋势下有微小的波动产生。列车运行速度对轮轨动力指标的影响规律与余弦型谐波不平顺的影响规律类似,随着列车运行速度的增大,轮轨垂向力和轮重减载率均呈非线性规律增大。
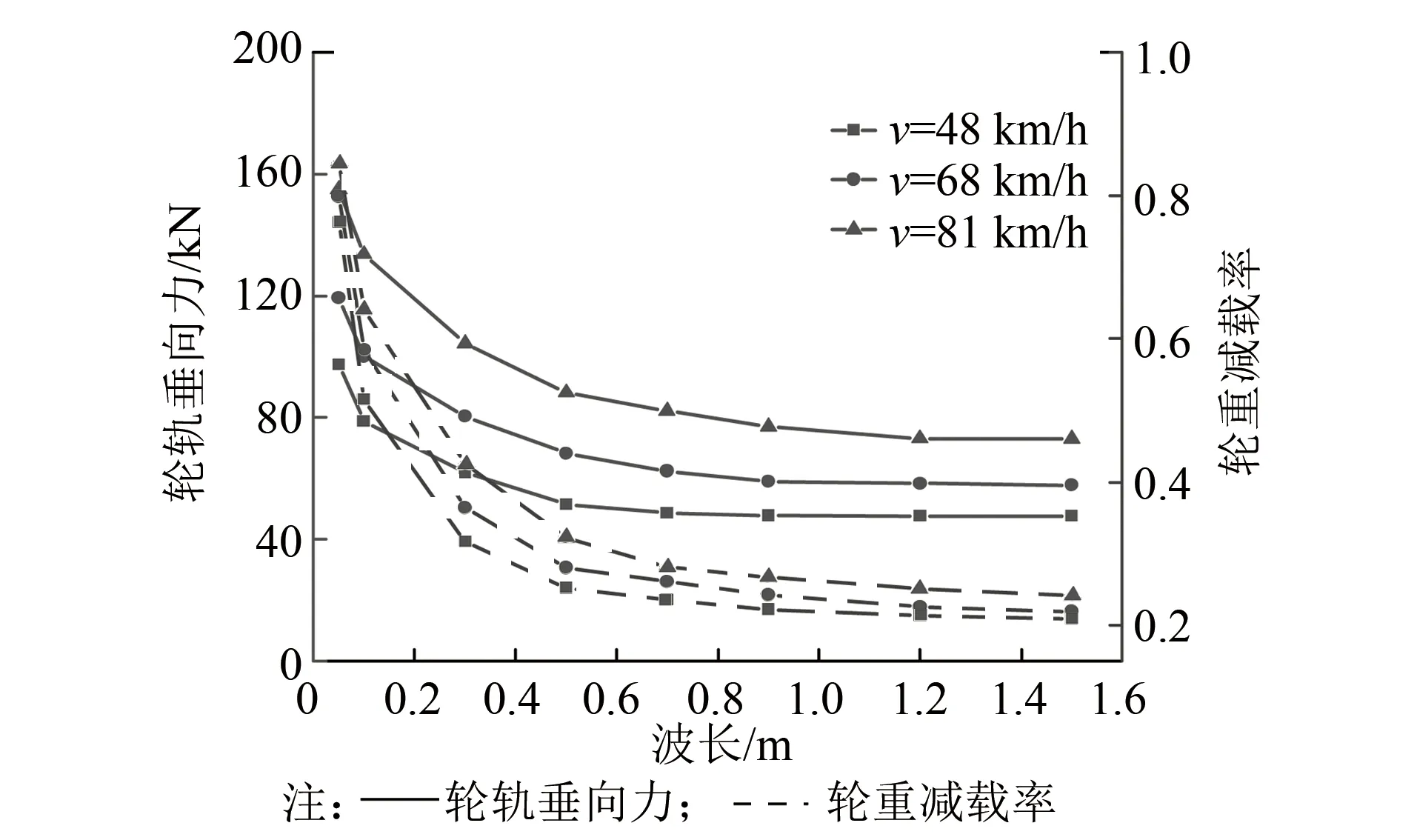
图5 余弦型不平顺波长对轮轨动力影响
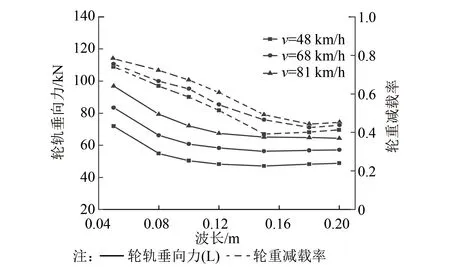
图6 λ1对轮轨的动力影响
2.2 短波波深对轮轨动力影响
图7和图8分别为不同速度工况下钢轨焊接接头余弦型谐波不平顺和叠加型短波不平顺激扰下波深对轮轨动力影响规律。其中,余弦型谐波不平顺固定波长λ0=1.0 m,叠加型不平顺λ1=0.1 m,λ2=1.0 m,长波波深a1=0.30 mm。
由图7可知,相同速度条件下,余弦型谐波不平顺激扰下轮轨垂向力随a2的增大近似呈线性规律增大。这表明:较大的波深会引起剧烈的轮轨相互动力作用,并且轮重减载率会随轮轨垂向力的增大而增大;相同速度条件下,轮重减载率也会随波深的增大而增大,且波深的影响明显大于轮轨垂向力。因此,轮重减载率便成为轮轨相互动力作用的主要控制指标。当a2>0.70 mm时,轮重减载率最大值已超过0.6,此时对车辆的曲线通过安全性造成不利影响。由图8可知,在叠加型短波不平顺激扰下,轮轨垂向力和轮重减载率均随a2的增大而增大。这与余弦型谐波不平顺激扰类似。不同的是,相对余弦型谐波不平顺激扰,叠加型短波不平顺激扰下的轮轨垂向力指标增幅明显更大。这可以认为是在叠加型短波不平顺的剧烈激扰下造成的。当车辆过曲线速度为81 km/h时,叠加型短波不平顺a2超过0.24 mm时,轮轨冲击力明显,对行车安全性产生不利影响。

图7 余弦型不平顺波深对轮轨动力响应的影响

图8 叠加型不平顺短波波深对轮轨动力响应的影响
2.3 两种不平顺对轮轨动力影响对比
为了研究在两种不平顺激扰下钢轨焊接接头引起的轮轨动力响应差异,余弦型谐波不平顺(简称“模型一”)取λ0=1.0 m,a0=0.30 mm;叠加型短波不平顺(简称“模型二”)取λ1=1.0 m,a1=0.30 mm,λ2=0.1 m,a2=0.10 mm。
当列车以68 km/h恒定速度通过曲线段时,钢轨焊接接头在两种不平顺激扰下的轮轨系统动力响应曲线如图9所示。由图9表明:两种不平顺激扰均会引起明显的轮轨冲击效应;无论是轮轨垂向力指标还是轮重减载率指标,受叠加型短波不平顺的影响均明显大于余弦型谐波不平顺。

图9 焊接接头不平顺激扰对轮轨动力作用影响
由此可知,两种不平顺激扰引起的轮轨动力响应差异显著,无论是轮轨垂向力、轮重减载率还是轮对垂向振动加速度,叠加型短波不平顺激扰均明显大于余弦型谐波不平顺激扰。因此,在城市轨道交通钢轨焊接接头不平顺理论研究中,采用叠加型短波不平顺激扰更为合理。
3 维修标准验证
目前,根据GB 50157—2013《地铁设计规范》要求,对于钢轨焊接接头不平顺,在1 m直尺测量矢度条件下,车辆运行速度大于120 km/h时,其不平顺幅值不超过0.30 mm,车辆运行速度小于或者等于120 km/h时,其不平顺幅值不超过0.50 mm。
为验证维修标准,选用1.0 m长波叠加短波钢轨焊接接头不平顺为激扰,对城市轨道交通曲线段钢轨焊接接头不平顺进行安全限值研究,分析结果如表1所示。
由表1可知,当a1>0.20 mm时,轮轨动力参数变化幅度较大,但轮重减载率及轮对垂向振动加速度均未超过最大安全限值;当a1=0.30 mm时,轮重减载率最大值为0.59,当a1=0.35 mm时轮重减载率达到了0.61,已经超过了轮重减载率最大安全限值0.6[16]。因此,当钢轨焊接接头不平顺采用叠加型短波不平顺时,不平顺最大幅值(即a1+a2)应不超过0.60 mm。这对于城市轨道交通线路来说是要求较高的。

表1 叠加型不平顺短波波深对轮轨动力响应的影响
4 结语
本文针对城市轨道交通曲线段钢轨焊接接头不平顺问题,运用车辆-轨道耦合动力学理论,从理论上分析了钢轨焊接接头不平顺对轮轨动力响应及车辆稳定性影响特征,分析了不平顺参数对轮轨动力学响应影响规律,并在此基础上,对现行规定的不平顺安全限值进行了验证评价。得出如下主要结论:
1) 曲线段钢轨焊接接头不平顺会引起较大的轮轨冲击力,无论是余弦型谐波不平顺还是叠加型短波不平顺,对轮轨动力响应的影响均随不平顺波长的增大而减小,随波深的增大而增大,而且行车速度越高,轮轨动力响应越显著。
2) 曲线段钢轨焊接接头不平顺最大安全幅值随行车速度的增大而减小,随不平顺波长的增大而增大;在曲线过超高条件下,余弦型焊接接头不平顺(1 m直尺测量条件下)最大安全幅值应不超过0.70 mm。
3) 曲线段叠加型焊接接头不平顺最大安全幅值主要受短波不平顺成分的影响,即1 m长波幅值为0.30 mm时,其短波(0.20 m波长)不平顺最大安全幅值为0.24 mm。
4) 通过对曲线段两种典型不平顺的对比分析发现,叠加型短波不平顺对轮轨动力响应的影响更为显著。
5) 验证评测结果表明,现有《地铁设计规范》规定的0.50 mm钢轨焊接接头不平顺安全限值对于城市轨道交通线路来说是过于严格的。在充分考虑行车安全储备前提下,该安全限值是否可调整尚需进一步研究。
