现代有轨电车嵌入式轨道结构力学性能分析
2019-10-16冯青松谢发明刘庆杰
冯青松 谢发明 孙 魁 刘庆杰
(1.华东交通大学铁路环境振动与噪声教育部工程研究中心,330013,南昌;2.苏交科集团股份有限公司,210019,南京//第一作者,硕士研究生)
现代有轨电车嵌入式轨道结构主要由槽型钢轨、填充材料、PVC(聚氯乙烯)管、弹性垫板及轨道板等结构组成[1-3]。其中,常用的填充材料为聚氨酯,是一种高度非弹性的高分子材料[4]。为了研究嵌入式轨道力学性能,需建立一种能体现填充材料力学特性的本构模型。
目前,基于填充材料线性本构模型对现代有轨电车轨道结构静力学和动力学特性等方面的相关研究有很多。文献[5-8]在对承轨槽内填充材料进行参数分析时,均将弹性体视为线性体,未能充分考虑改性聚氨酯填充材料的非线性对轨道结构力学特性的影响。国内外对承轨槽内填充材料按非线性考虑的研究还比较少。为此,本文建立填充材料的非线性模型及线性模型,分析不同模型对轨道力学性能的影响。
1 计算模型及参数
本文采用ABAQUS有限元软件来分析嵌入式轨道结构的非线性力学性能。所研究的轨道结构主要由60R2槽型轨、填充材料聚氨酯、PVC管及轨道板等组成。
1.1 填充材料的本构模型
硬度不同的聚氨酯弹性体,其弹性模量取值不同。本文取硬度分别为70~72 A和43 A的两种聚氨酯材料作为试样,进行单轴压缩试验。相关试验数据如表1所示。

表1 聚氨酯试样单轴压缩试验结果
聚氨酯非线性弹性体需通过应变能密度函数来描述其材料的非线性弹性特征。构建超弹性材料本构模型可使用基于统计理论的本构模型和基于唯象理论的本构模型。基于已有的聚氨酯单轴压缩试验数据,使用唯象理论来描述超弹性材料性质是最简单的途径。在拟合填充材料本构模型时,应变能函数采用Polynomial和Ogden本构模型。其中,Polynomial多项式的应变能函数表达式为:
式中:
W——应变能函数;
N——多项式阶数;
i、j——Polynomial多项式参数;
Cij——同温度有关的材料参数Rivlin因数;
Di——弹性体的介电常数;
R——弹性体稳定性系数;
I1c——第一偏应变不变量;
I2c——第二偏应变不变量;
Jc——变形后与变形前的体积比,Jc=λxλyλz,其中λx、λy和λz分别为为主伸张率,下标x、y和z分别表示3个相互正交的方向。
Ogden应变能函数的表达式为:
式中:
αi——弹性体材料的应变硬化指数,通过试验确定;
υi——弹性体材料的剪切模量。
αi、υi、Di和R是与温度有关的材料参数。它们的数值由聚氨酯材料的单轴压缩数据确定。其中,幂指数αi能拟合完全非线性试验数据的任意实数[9-10]。
根据聚氨酯弹性体应力应变性能试验数据,利用ABAQUS软件中的材料模块功能,可获得适合嵌入式轨道填充材料非线性本构关系。两种聚氨酯弹性体的非线性本构模型可分别用多项式函数(N=2)和Ogden函数(N=5)来拟合,相应的应变能拟合曲线如图1所示。由拟合结果可见,两种非线性本构模型均具有较好的匹配度和稳定性。

图1 承轨槽内浇筑的改性聚氨酯填充材料本构模型应变能拟合曲线
1.2 非线性本构模型的正确性验证
在ABAQUS软件中建立了与实际试验试件大小相同的有限元模型,通过试验数据与仿真结果的对比,来验证填充材料非线性本构模型的合理性。应力与应变关系的试验结果及仿真数据如图2所示。
由图2可知,两种聚氨酯材料的仿真应变值与实际试验应变值最大相差5%。可见,误差比较小,仿真结果与实际试验结果近似相等。因此,采用试验与仿真相结合的方法足以验证嵌入式轨道填充材料非线性本构模型的正确性。
1.3 计算工况
嵌入式轨道尺寸为5.00 m×1.05 m,轨道板竖直部分高度为180 mm,承轨槽结构平面尺寸为220 mm×200 mm。在ABAQUS有限元软件中建立三维实体有限元模型,如图3所示。轨道结构参数如表2所示。

图3 嵌入式轨道有限元模型
有轨电车实际行驶速度较低,有轨电车最大轴重为12.5 t[11],安全系数取值为1.12。计算模型中,竖向荷载取70 kN,横向荷载Q=0.6PJ=42 kN。竖向荷载施加于轨顶正中心线上,横向荷载施加在轨顶面以下14 mm处。在有限元模型中,约束轨道板的两端及底面,将槽型轨与填充材料的接触方式设为绑定接触,将填充材料与混凝土的接触方式设为为绑定接触。在进行网格划分时,槽型轨、轨道板及PVC管网格划分采用实体单元C3D8R[12]。由于轨底没有使用弹性垫板,将承轨槽内轨底填充材料按厚度分为20 mm、30 mm和40 mm等3种工况。使用基于填充材料非线性及线性本构模型按工况进行轨道力学性能分析。
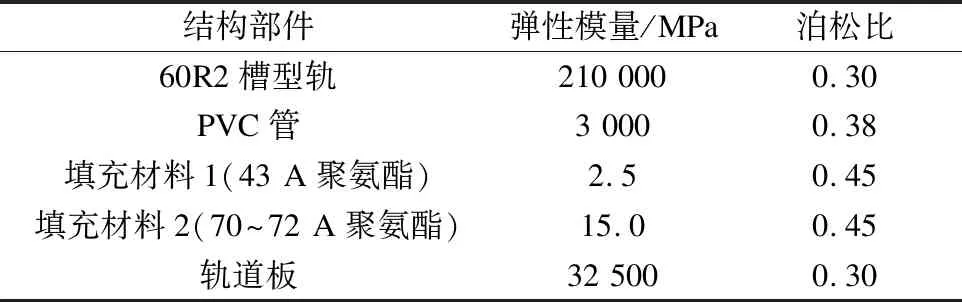
表2 轨道结构参数
在线性本构模型分析中,聚氨酯弹性体的弹性模量按表3取值。
2 非线性模型与线性模型结果对比分析
由计算结果可得,非线性模型与线性模型钢轨竖向位移计算结果相差不大,填充材料的非线性特征对其位移影响较小。
表3为通过非线性本构模型及线性本构模型,对不同聚氨酯填充材料、不同工况下,轨道结构各部分应力计算的仿真结果。根据表3可得:对填充材料的应力极值,两种模型的仿真结果相差10%左右;对PVC管应力极值,两种模型的仿真结果相差8%左右。

表3 轨道结构各部分应力极值的仿真计算结果
3 不同PVC管直径对钢轨位移的影响
3.1 计算模型
本文按5种不同工况,分析PVC管直径对钢轨位移的影响。不同工况的模型如图4所示。
3.2 模型参数
模型长度取5 m,不设置弹性垫板。承轨槽截面尺寸为220 mm×200 mm,轨底填充材料厚度为20 mm。承轨槽结构模型中,60R2槽型轨及PVC管的参数取值见表2,填充材料弹性模量取2~20 MPa、泊松比取0.45。
承轨槽结构底面及两侧施加全约束,网格单元选择C3D8R。经计算,竖向荷载为70 kN,横向荷载为42 kN。竖向荷载施加在模型中间钢轨中心线处,横向荷载施加在轨顶面以下14 mm处。
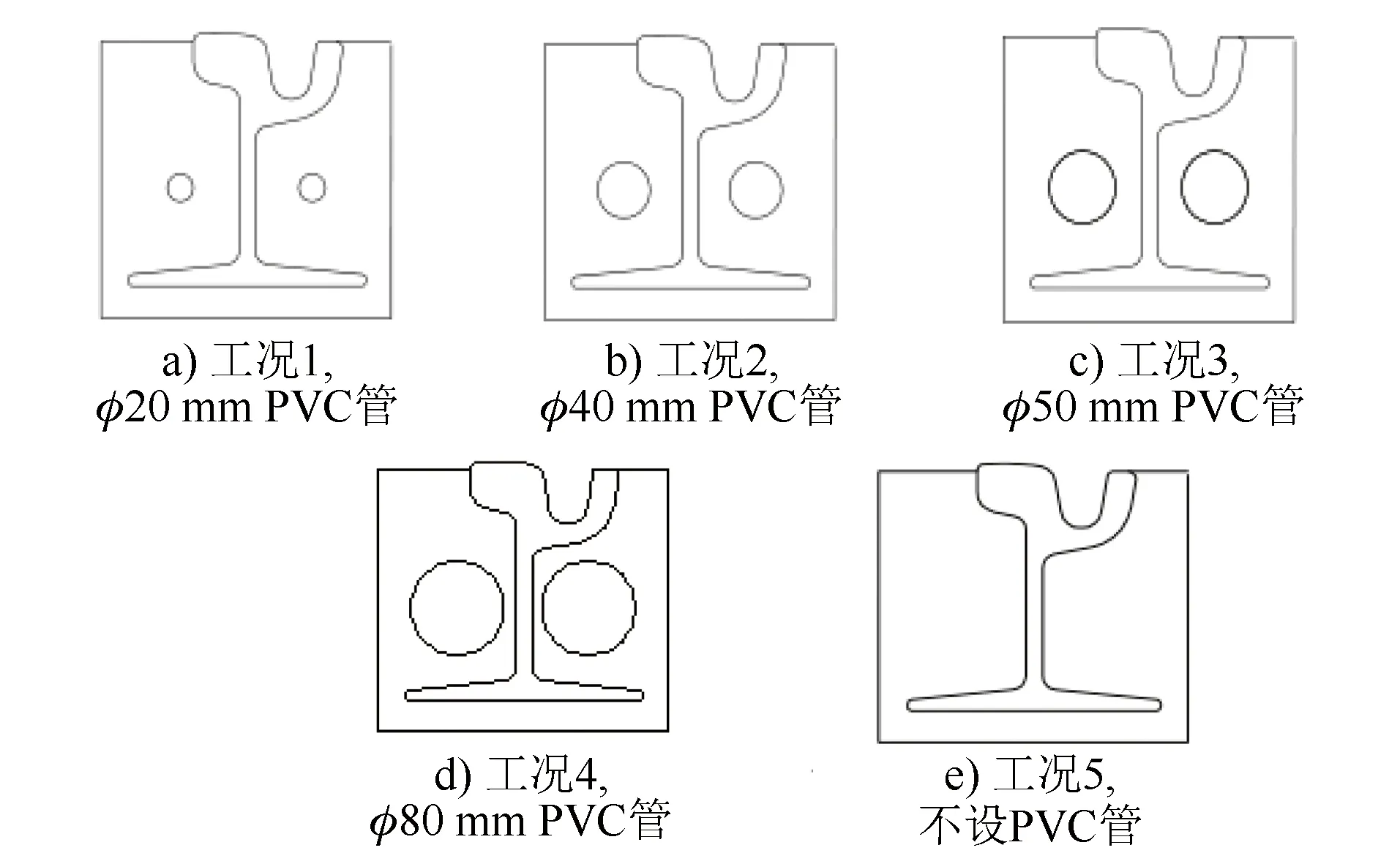
图4 不同工况的承轨槽计算模型横断面示意图
3.3 承轨槽结构受力分析
图5~6为不同PVC管的直径对钢轨位移值及填充材料应力影响的计算结果。
由图6可知,改变PVC管的直径对钢轨位移模型没有影响,不同工况的影响曲线基本都是重合。

图5 不同直径PVC管对钢轨位移的影响
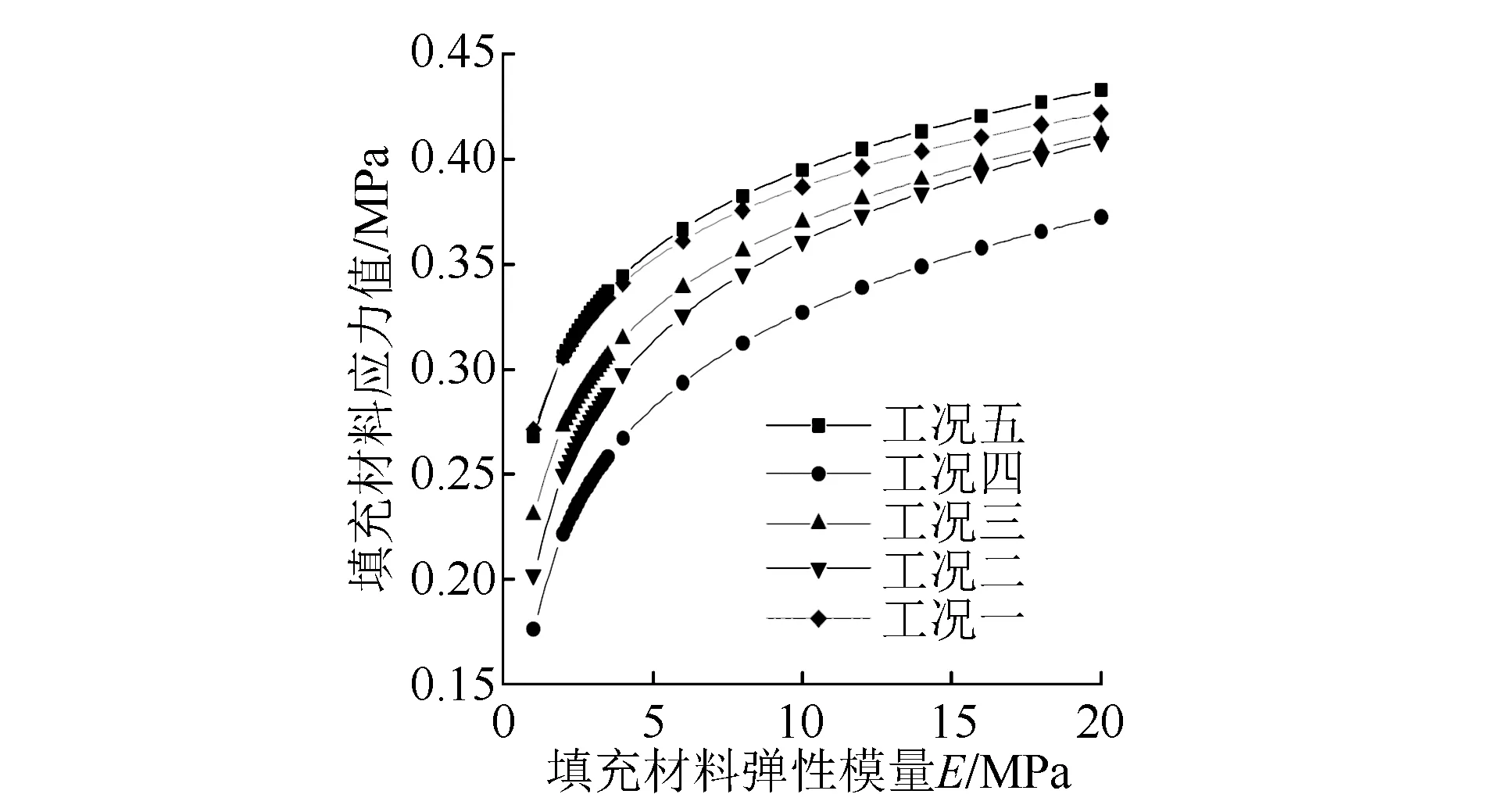
图6 不同直径PVC管对填充材料应力的影响
由图5可知,改变PVC管的直径,对填充材料的应力会有一定的影响。工况1与工况5填充材料的应力值相同,且随着填充材料弹性模量的增大,不同工况的曲线基本重合在一起。可见,可以通过设置PVC管来节省填充材料。
4 结论
本文结合填充材料试验数据,拟合了嵌入式轨道填充材料的非线性本构模型,得到如下主要结论:
1) 采用线性本构模型与非线性本构模型,得到的轨道力学性能分析结果相近。因此,建议在进行嵌入式轨道结构受力分析时,可将聚氨酯材料视为线弹性体,以简化计算。
2) 嵌入式轨道承轨槽内填充材料的硬度对钢轨位移有较大影响。相比填充材料弹性模量为2.5 MPa时,当填充材料弹性模量为15 MPa时的钢轨竖向位移及横向位移小约为50%。
3) 轨底填充材料厚度对轨道力学性能影响较小。改变槽型轨轨底填充材料厚度,轨道位移及应力变化幅度均小于5%。
4) 在轨底填充材料厚度及开槽宽度相保持不变的情况下, PVC管的直径对钢轨位移影响较小。使用PVC管可节省填充材料,减少工程造价。
