推理能力——数学学习的“金钥匙”

江苏无锡市新吴区旺庄实验小学 钱 慧

推理是指人们根据已有的知识，凭着自身的经验和直觉，通过分析与综合、类比与归纳的方法，推论出新知识的过程。推理一般包括合情推理和演绎推理。推理能力是指以敏锐的观察比较、简捷的分析思考，快捷地抓住问题的核心，在最短时间内做出合理正确的选择。推理能力是人们解决问题的必备能力，人们良好的推理能力是进行有理有据推理的前提保障。推理能力并不是与生俱来的，需要在后天的学习过程中逐渐养成。小学阶段是学生各种能力的启蒙发展阶段，数学是小学各学科中最适合培养学生推理能力的一门课程。《义务教育数学课程标准（2011年版）》指出，推理是数学的基本思维方式，是人们学习和生活中经常使用的思维方式，它贯穿于整个数学学习中，教师要从学生的已有经验出发，通过有效的方法培养学生的推理能力。

一、在情境中激发学生的推理意识

教学情境是指教师在课堂教学环境中，根据学习内容，让学生引起主动学习情感态度反应的教学过程。课堂上教师综合利用各种教学手段通过有意义的教学活动行为，创设一种学习氛围，让学生形成良好的求知心理，参与对所学知识的认知、探索和推理的过程。数学情境是指教师在数学教学过程中，结合课堂教学的核心内容，创设一种教学场景，模仿问题发生和发现的过程，有利于数学问题的形成，让学生的思维积极主动，在知识冲突中激发学生想推理的思想，让学生的学习变为“我要学”“我要推理”，发展学生推理意识，训练学生的直觉思维，从而让学生更有效地参与学习。

例如，苏教版小学数学六年级上册“表面涂色的正方体”，课前教师播放魔方高手成才的视频，他从简单的三阶魔方玩起，熟练了再来研究高阶魔方，从而成了魔方高手。为什么先玩三阶魔方？这一问题引发学生得出了“从简单入手，找出规律再来解决复杂问题”的数学思维方式。课始出示“汤姆和杰米追打的动画场景”，杰米一不小心打翻了一个表面涂色的大正方体魔方，他们想办法还原，但是还原不了。“有什么问题吗？”“因为涂色面数不同，小正方体不能随便放。”教师用一串问题来引导学生思考回答：有哪些涂色情况？（三面涂色、两面涂色、一面涂色、没有涂色）这个正方体的每条棱平均分成了8份，三面涂色、两面涂色、一面涂色、没有涂色的小正方体在哪儿？各有多少个？表面涂色的正方体中有怎样的规律呢？（学生露出迷茫的表情），这个大正方体太大了，我们可以怎样来研究？学生受到魔方高手视频的启发，积极举手回答：从简单入手，可以先研究小一点的正方体。先来研究每条棱平均分成2份的正方体（出示图），展开推理探索活动。

这种充满灵气的动画情境，激发了学生学习数学的学习热情，充分调动了学生的积极推理思考的欲望。教师通过创设“魔方天才成才”和“汤姆、杰米打翻大正方体魔方”的动画情境，激发学生的学习兴趣，通过真人真事唤起学生数学学习中也要有这种“从简单入手”的好的推理意识。这样的情境，不仅给学生学习新知做好了坚实的铺垫，更主要的是，学习的内容已经深深触动到了学生的心灵深处，他们在情境中思考、推理、成长，促进了学生数学内容的迁移，从而更主动地学习。

二、在探究中训练学生的推理方法

数学中的探究是学生们结合一些数学核心问题，利用个体或小组合作的形式，在具体生动的数学学习情境中，通过尝试、实验、自学等学习方式，发现问题，分析问题，寻找解决问题的策略方法，获取新的知识，形成数学推理能力的活动。在教学时，教师要善于引导学生经历观察、实验、猜想、验证、推理、交流等数学探究学习过程，将知识转化为可以运用的数学理论，学生通过动手实践、合作交流、自主探索，运用合理的推理方法分析问题，解决问题，感悟数学学习的方法，在动手、动脑、动口中培养良好的逻辑推理能力。

例如，苏教版小学数学五年级上册“平行四边形的面积”一课，教师安排了以下推理过程：

1.在变化中提出猜想

教师出示长方形框架长6厘米，宽5厘米，面积是多少呢？（5×6=30平方厘米）教师拉动长方形木框变成一个平行四边形，猜猜它的面积是多少呢？有些同学猜是30平方厘米，用两邻边相乘求出它的面积；一部分同学猜想不是两邻边相乘，应该是底×高。教师继续拉动木框，木框越来越倾斜，现在这个平行四边形的面积还有30平方厘米吗？平行四边形的面积明显越来越小，大部分同学都认为不能用两邻边相乘求面积。

2.在操作中验证公式

（1）数一数，下面图形的面积是多少？

（2）剪一剪，拼一拼，你能把下面的平行四边形转化成什么图形？

（3）说一说，推理出平行四边形的面积怎样计算。

学生在实际操作中，通过数一数三个图形的面积，更加确信平行四边形的面积不等于邻边相乘；经过剪拼的过程，学生发现了平行四边形与长方形之间的关系，验证并推导出了平行四边形的面积计算公式。操作探究更形象、更直观、更有说服力，学生通过猜想、画图、转化等操作探究活动不断积累推理的方法。

三、在问题解决中提升学生的推理素养

问题解决是指借助一定的认知活动、技能方法等，经过一些具体的思维、操作，达到某种目标，最终使问题得以解决的过程。学生的数学学习就是利用所学的知识解决问题的过程，学生数学学习的最终目的就是能运用所学的知识解决问题，学会学习。在小学数学教学中，要培养学生的推理能力，就必须拓宽学生的数学学习的思维方式，让他们学会利用这些思维方式进行思考与推理。教师要精细设计有梯度的问题练习，让学生通过解决问题不断摸索问题解决的捷径，通过有层次的拓展训练，让学生进入推理思维的最佳境界，在问题解决过程中，迁移深化，由表及里，提升推理能力，发展数学核心素养。

例如，学生在解决“1+3+5+7+9+……+99=？”这种复杂问题时，教师要首先引导学生运用“从简单入手”的推理方法，1+3=4=22，1+3+5=9=32，1+3+5+7=16=42，学生通过观察比较几个简单的算式推理出：几个连续奇数的和等于一个数的平方。接着教师引导学生利用方格图进行深入推理：

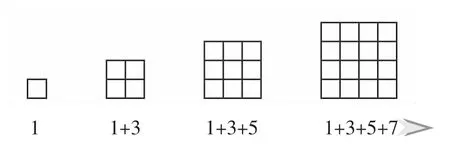
学生结合图和算式，合情推导出：计算从1开始几个连续奇数的和就是计算对应正方形的面积，关键是要找到正方形的边长，学生观察发现后得出：边长=（尾数+1）÷2，所以，1+3+5+7+9+…+99=[（99+1）÷2]2=2500，进而得出：1+3+5+7+9+……+n=[（n+1）÷2]2。然后让学生完成：2+4+6+8+…+100=？学生运用已有的推理经验很快得出：

从2开始连续偶数的和，就是求对应长方形的面积，长方形的长比宽多1，宽等于尾数÷2，所以，2+4+6+8+…+100=（100÷2）×（100÷2+1）=50×51=2550，进而得出2+4+6+8+…+n=（n÷2）×（n÷2+1）

学生在解决问题的过程中，合情推理有助于探究出解决问题的思路与方法，学生运用“图形结合”的数学思想，不断积累推理的经验，让自己的推理印象深刻，逻辑清晰。学生不仅能够自己发现解决问题的策略，而且可以利用自己发现的策略去促进他们的数学理解。教师为学生的思维碰撞搭建舞台，让学生在多变的问题中实时地进行推理，感悟在单一方法中寻求多样化，在多样化背后寻求内在联系的意义，训练学生的推理素养。

在数学教学中对学生进行推理能力的培养，对于教师来说可以提高课堂效率，增加课堂教学的趣味性，优化教学条件，提升教学水平和业务水平。对于学生来说，推理能力不但能使他们学到知识，会解决问题，而且能掌握在新问题出现时如何应对的思想方法。教师要紧紧抓住数学学习的“金钥匙”——推理能力，让学生积极地参与数学活动，体会数学知识的形成过程，感悟到推理的方法和效能，充分展现想象能力和抽象能力，发展数学逻辑思维能力。♪