美国膨胀节制造商协会标准圆形波纹管膨胀节应力计算原理及其拓展推广计算

，

(自由职业， 江苏 南京 210000)

波纹管膨胀节是压力管道上常用的设备，其核心部件波纹管的设计相对复杂。波纹管不仅要满足强度指标，还要符合疲劳寿命、刚度、稳定性等要求，设计时必须予以兼顾。膨胀节通常按照标准设计，膨胀节国际标准较多，其中以美国膨胀节制造商协会标准(EJMA标准)应用范围为最广，国内主要的膨胀节标准GB/T 12777—2008《金属波纹管膨胀节通用技术条件》也是吸收EJMA标准并有所创新，与EJMA标准相互补充[1-4]。

随着工业技术的进步，波纹管膨胀节的使用工况变得复杂。在石油化工管道中使用的膨胀节，由于介质成分比较复杂，常会出现波纹管与介质接触层采用高性能的材料，其他层采用较为普通的材料来设计、制造波纹管，并且这一设计方式有向其他行业扩展的趋势，如钢铁行业。目前多种材料制作的波纹管的设计计算还未标准化，不能满足工业生产的实际需要。

文中分析和探讨了EJMA标准中加强和无加强圆形波纹管的计算原理，并对EJMA标准计算原理进行推广，推导出了2种不同材料制作的波纹管的应力计算公式[5]。本中分析基础采用EJMA第九版2011增补，文中未特别说明的物理量含义与EJMA中的相同。

1 EJMA标准圆形波纹管计算原理

1.1 无加强型波纹管应力计算

1.1.1波纹管直边段环向膜应力S1和套箍环向膜应力S1′

波纹管直边段与套箍承受的力之和为波纹管总受力，且符合变形协调条件，其周向应变相等。总受力F1为：

F1=p(Db+nt)Lt

式中，p为设计压力；Db为波纹管直边段内径；n为波纹管层数；t为波纹管单层壁厚；Lt为波纹管直边段长度。

已知波纹管直边段截面积为ntLt,套箍截面积为Lctc(Lc为套箍长度，tc为套箍厚度)。根据应变=应力/弹性模量[6]，可得方程组：

解此方程组,得：

(1)

(2)

EJMA标准对式(1)和式(2)进行修正，修正方法为分子分母同时乘以Db+nt，然后使用套箍平均直径Dc代替式中套箍项Db+nt，并且分子和分母均乘以修正系数k，得出最终计算式：

1.1.2压力在波纹管中产生的环向膜应力S2

S2计算原理与压力容器周向膜应力计算原理[7]基本相同，区别是吸收位移后波纹管的受压长度将会发生变化。单波受力F2=pDmL。其中，Dm为波纹管有效直径；L为波纹管单波轴向受压长度，取整个运动过程中出现的最大值。 EJMA标准中，L=qKr。其中，q为波距，Kr为周向应力系数(拉伸会使位移增大L，式中的Kr随之增大)。

S2按下式计算式：

1.1.3压力引起的子午向膜应力S3及子午向弯曲应力S4

《波形膨胀节实用技术》[8]中给出了无加强波纹管的S3、S4计算的基本模型。EJMA标准采用两端固支直梁受线性均布载荷作用的模型模拟波纹管受压工况，梁长度为W(即波高)，梁宽度为πDm(波纹管周向展开长)，梁高为tp(材料壁厚)。梁的受力F3和力矩M1的最大点在梁的两端，S3和S4按下式计算(F3、M1算式在材料力学[9]中查出)。

EJMA标准对S4增加了修正系数Cp，S4计算式修正为：

1.1.4单波当量轴向位移e在波纹管中产生的子午向膜应力S5及子午向弯曲应力S6

文献[8]中也给出了无加强波纹管的S5、S6计算基本模型。EJMA标准依然采用上文1.1.3所述两端固支直梁模型，其一端发生e/2的偏移(1个波纹管相当于2个并列的梁)。梁的受力F4和力矩M2最大点在梁两端，S5和S6按下式计算(F4、M2算式可在材料强度力学[10]中查出)。

对S5、S6，EJMA标准分别增加了修正系数Cf、Cd，并且把S6的系数3/2修正成5/3，得到S5和S6最终计算式：

1.1.5单波理论轴向刚度fi

(3)

式(3)是1层波纹管的单波理论轴向刚度计算式。如波纹管为多层结构，则只要乘以层数n即可。

1.1.6柱状失稳压力psc

EJMA标准计算柱状失稳压力psc时使用的模型把波纹管当量成两端固定的细长压杆,此杆直径为波纹管有效直径Dm，杆长等于波纹管长度Lb,波纹管波数为N，波纹管波距为q,此细长压杆的临界压力Fcr按下式计算[11]：

(4)

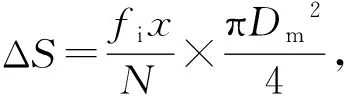
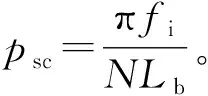
1.2 加强型波纹管应力计算

1.2.1波纹管直边段环向膜应力S1j及套箍环向膜应力S1j′

加强型波纹管的S1j、S1j′计算原理和无加强型波纹管的基本一样，区别就是轴向受力长度取值发生了变化，其取值变成Lt+q/2，波纹管和套箍的金属截面积相应变化，受压长度范围内的所有金属面积都被计入，则波纹管截面积变成nLtt+Ac/2 (Ac为单波截面积)，套箍截面积变成套箍面积+铠装环面积，统一记成Atc。S1j和S1j′的最终公式为：

需要说明的是，考虑到国内普遍将套箍和波纹管的直边段焊接在一起的做法使得套箍环向弯曲应力无太大实际意义，本文对EJMA标准中套箍环向弯曲应力不作进一步讨论。

1.2.2整体型铠装环压力在波纹管中产生的环向膜应力S2j和压力在铠装环中产生的环向膜应力S2j′

波纹管加强铠装环分为整体连接型和螺栓连接型，这2种连接方式的计算有一定区别。下面针对EJMA标准中给出的整体连接铠装环的应力计算过程进行分析。计算基础依然与容器膜应力计算理论一样，容器的总受力为pDL，其中受压长度L=qKr。采用EJMA标准中变量H来代表总受力，H=pDmqKr(EJMA标准中H并未包含Kr。为方便起见，文中H均包含Kr)，铠装环截面积为Ar，铠装环材料弹性模量为Er。

根据变形协调条件和受力平衡条件可以列出方程组[13]：

解此方程组，得基础计算式：

(5)

(6)

同理，对式(6)进行调整，分子分母同时除以ArEr，有：

(7)

加强型波纹管最终计算公式是仅基于把铠装环看成材料和壁厚不同的一层波纹管(后面推广分析不同材料组合成的波纹管时亦会证明此点)的假设得到的理论推导式，EJMA标准未做进一步的修正。

1.2.3螺栓连接型铠装环压力在波纹管中产生的环向膜应力S2jl、压力在铠装环中产生的环向膜应力S2jl′、压力在连接螺栓产生的应力S2jl″

螺栓连接铠装环的径向长度等于铠装环本体长度Dm与螺栓有效长度Lf之和，即Dm+Lf，螺栓连接铠装环受力径向长度示意图见图1。

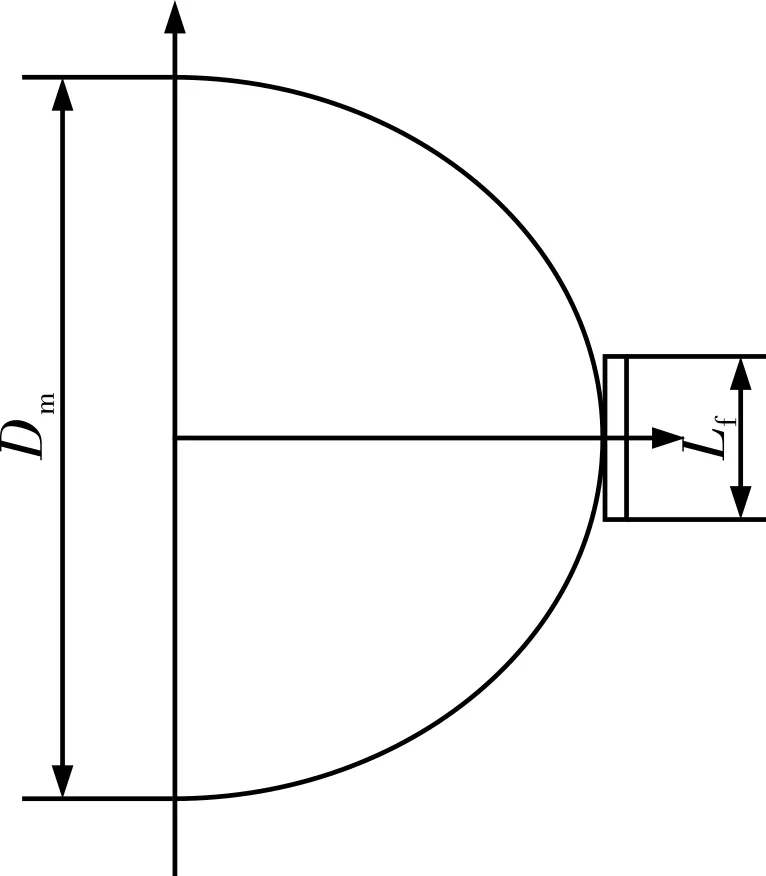
图1 螺栓连接铠装环受力径向长度示图

螺栓连接铠装环径向受压长度与波纹管不同，即铠装环组件和波纹管的应变ε不再一样。只能通过径向绝对伸长量相同来计算，伸长量为Δ。由于Δ=εL且ε=S/E，则Δ=SL/E。铠装环主体伸长量和螺栓伸长量之和等于波纹管伸长量，则有方程组：

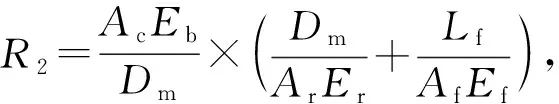
对比1.2.2节式(7)可知，螺栓连接的铠装环加强的波纹管承受的力会增大，其增大量与螺栓长度和截面积有关。而铠装环的应力会相应减小，但是此应力状态只发生在螺栓所在这一特定截面上，在其他截面铠装环还是相当于整体连接的，特别是与此90°垂直的截面，因此铠装环应力需要取大的点，即S2jl′的值要用式(7)计算。

1.2.4S3j、S4j、S5j、S6j、fij、pscj

铠装环加强型波纹管这些参数的计算原理与无加强波纹管只有一点区别。由于铠装环的存在，波纹管的一部分紧贴在铠装环上，不再参与位移工作和受力，导致计算模型的梁长度变短了，EJMA标准把计算波高调整为W-4Crrm，其中rm为波纹管波纹平均半径，Cr为和压力有关的波高系数。简单理解就是压力越大，波纹紧贴到铠装环上的部分越多，梁长损失越多。压力从0到无穷大，Cr相应从0.2增大至0.3(压力小于0应该按0处理)。EJMA标准第十版更改了这一波高修改算法，取消了Cr[14]，这和本文分析原理关系不大，相当于一个系数，只要按照EJMA标准取值即可。

另外，对于S3j、S4j的计算，EJMA标准还增加了修正系数0.85、将pscj计算式中系数0.34调整为0.3等。

2 复合材质波纹管膨胀节应力计算公式推导

应用前述对标准圆形波纹管膨胀节计算原理的分析，针对由2种不同材料、壁厚组成的复合波纹管膨胀节进行应力计算公式的拓展性推导。所有参数基本含义与EJMA标准中相同，参数下标1表示常规材质层，2表示更换的材质层，例如Eb1、Eb2、n1、n2、S11、S12、S21、S22等。另外,Ac1、Ac2分别表示常规材料层和更换材料层的单波单层波纹管截面积；fi1、fi2分别表示常规材料层和更换材料层的单波单层理论轴向刚度；Ac表示单波总截面积，Ac=n1Ac1+n2Ac2；Ace表示单波总截面积弹性模量,Ace=n1Ac1Eb1+n2Ac2Eb2；y表示受线性均布力时梁的最大扰度。

2.1 波纹管直边段应力S11、S12、S1t′计算公式

2.1.1无加强型波纹管

依照本文第1部分中对无加强型波纹管应力计算所作的原理分析，令Dp=Db+n1t1+n2t2，则有方程组：

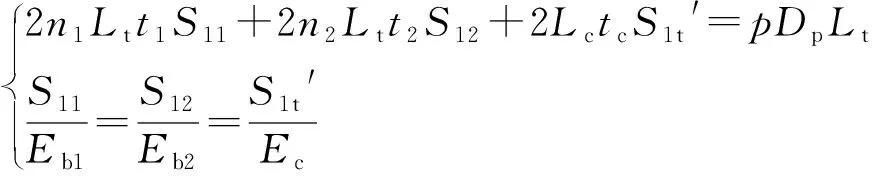
解此方程组得：

调整方法同1.1.1节，计算式分子分母同时乘以Db+nt，然后使用套箍平均直径Dc代替式中套箍项(Db+nt)，并且分子和分母均乘以修正系数k，得到由2种不同材料、壁厚组成的复合波纹管膨胀节的波纹管直边段应力S11、S12、S1t′最终计算公式如下：

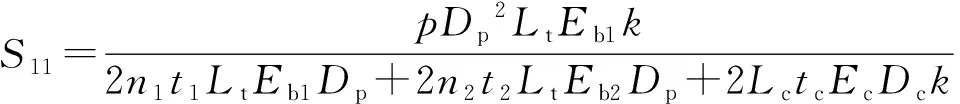
S11、S12、S1t′最终计算式中的系数k与波纹管材料壁厚有关。如果波纹管内不同壁厚材料组成，笔者建议按照常规层的壁厚取k值。

2.1.2加强型波纹管

应用本文第1部分中对加强型波纹管应力计算过程所作的原理分析，进行拓展性推导和调整，得到由2种不同材料、壁厚组成的复合材料圆形波纹管膨胀节的波纹管直边段应力S11j、S12j、S1jt′最终计算公式如下：

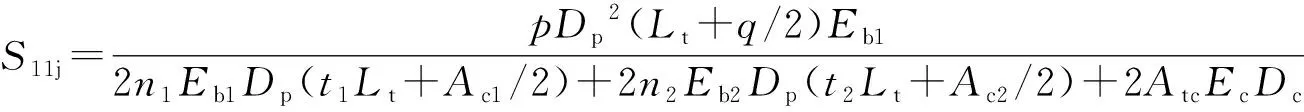
2.2 波纹管与铠装环环向应力S21、S22、S2jt′、S2jt″ 计算公式推导

2.2.1无加强波纹管

环向膜应力的计算原理是2种材料承受的力之和等于总力H，有方程组：

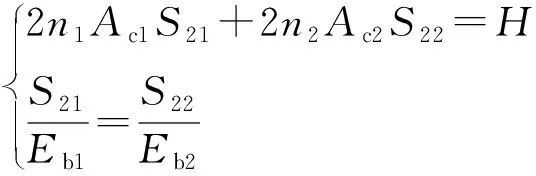
解此方程组得：

2.2.2整体连接铠装环加强波纹管

应用本文第1部分中对整体连接铠装环加强波纹管应力计算所作的原理分析进行拓展性推导，由2种不同材料、壁厚组成的复合波纹管膨胀节有方程组：

解此方程组可得波纹管与铠装环环向应力S21j、S22j、S2jt′基本计算如下：

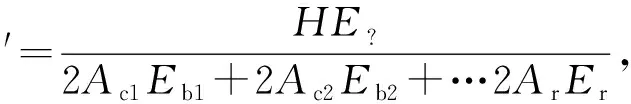
同理可得：

(8)

2.2.3螺栓连接铠装环环加强波纹管

对于由2种不同材料、壁厚组成的螺栓连接铠装环环加强波纹管，应用与本文第1部分相同的计算原理，用伸长量Δ相等进行计算(波纹管的2种材料符合应变相等的条件)，有方程组：

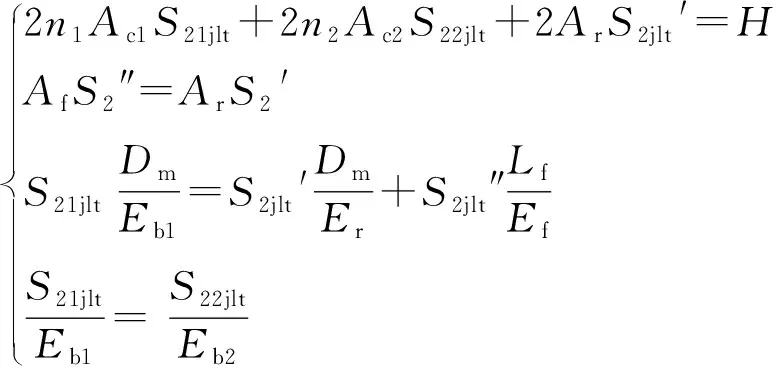
解此方程组得：

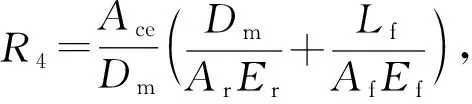
(9)

由式(9)可求出应力S21jlt最终计算式如下：

同理得：

出于对螺栓连接铠装环加强型波纹管的受力分析(与本文第1.2.3部分相同)，此处的环应力S2jit′相应地需改用式(8)进行计算。

2.3 波纹管子午向应力S31、S32、S41、S42计算公式推导

波纹管子午向应力的计算原理和本文第1部分分析的一样，但由于部分层材料和壁厚的改变，各层分担的分压力将不相同(同一材料时，每层的分压力是相同的)，因此要计算S31、S41、S32、S42，就需要先计算其分担的分压力，令分压力分别为p1、p2。两端固支直梁受线性均布力产生挠度示意图见图2。

图2中梁的挠度计算式见工程力学手册[15]，波纹管各层挠度y相同，则有：

图2 两端固支直梁受线性均布力产生挠度示图

解此方程组得：

(10)

(11)

根据式(10)、(11)，直接调用前面的计算方法，即可求出应力，本文不再继续推导，最终公式如下(括号内为加强型波纹管计算式,如果2种材料壁厚不一致，则系数Cp也不相同)：

2.4 S51、S52、S61、S62、fi1、fi2、fi、psct计算公式推导

对于位移引起的应力S51、S52、S61、S62以及波纹管各层单波轴向理论刚度fi1、fi2这些参数的计算，波纹管的各层相当于并联，相互间并不影响，因此使用EJMA标准的公式代入各自参数分别计算即可。而总单波轴向理论刚度只需把各层计算值相加即可，柱失稳压力psct亦可计算。结果罗列如下(括号内为加强型波纹管的计算式，如果2种波纹层壁厚不一致，则系数Cf、Cd也不相同)：

fi=n1fi1+n2fi2

2.5 平面失稳压力psi计算公式推导

对平面失稳压力psi的计算，笔者没有得出确切的计算模型和理论依据，只通过EJMA标准的公式进行反推。对EJMA标准psi公式进行调整，有：

(12)

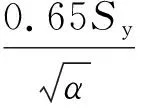
单独考虑各层，每一层分担到的分压力均不能超过单层平面失稳的压力，2种材料单层平面失稳压力分别为：

(13)

按照上面推论，平面失稳压力是由环向应力S2推导而来，就按照环向应力特性求解2种材料分压力p1′、p2′，有：

解此方程组得：

先按照第2种材料单层平面失稳压力psi2计算波纹管总平面失稳压力，有：

(14)

将式(14)带入式(13)得出按照第2种材料单层平面失稳压力算出的总平面失稳压力：

(15)

同样步骤，可以求出按第1种材料单层平面失稳压力算出的总平面失稳压力：

(16)

然后取式(15)、式(16)计算出的数值较小者即可得出最终平面失稳压力值。

3 结语

波纹管膨胀节在管线中使用情况变得越来越复杂，但是相应标准却略显滞后，特别是采用2种材料复合制造的波纹管越来越多的被应用，标准中却没有相应计算公式。本文通过分析EJMA标准的设计计算原理并按照原理进行推广，推导出了复合制造波纹管的计算公式，可以解决相应实际问题。