城轨回流系统动态排流与钢轨电位控制仿真研究

黄 蕾,杜贵府,王 俊,田 静

(苏州大学轨道交通学院,江苏苏州 215131)

城市轨道交通普遍采用直流750 V或1 500 V牵引供电方式，系统中一般采用走行轨作为牵引电流的回流通道，由于走行轨具有一定的纵向电阻，并且它无法做到完全与大地绝缘，会使得走行轨与大地之间形成钢轨电位，部分电流经走行轨泄漏至周边介质产生杂散电流，不可避免地会存在杂散电流过大与钢轨电位过高的问题[1]。

杂散电流会对城轨自身主体结构钢筋及周边埋地金属管线产生严重电化学腐蚀[2-3]，而钢轨电位会对乘客人身安全及轨旁设备造成损害，甚至会引起框架保护动作，导致线路大范围停电[4]。为了限制杂散电流与钢轨电位，回流系统中设置了排流装置与钢轨电位限制装置(OVPD)，但排流装置与OVPD的动作特性直接决定了系统钢轨电位与杂散电流的控制效果[5]。文献[6-8]在建立杂散电流与钢轨电位仿真模型时，一般以静态模型分析杂散电流与钢轨电位的分布，同时难以计及OVPD与排流装置的动态控制特性分析系统相关参数的动态变化。由于计及排流装置与OVPD的回流系统杂散电流与钢轨电位动态仿真方法缺失，导致系统排流和OVPD控制下杂散电流与钢轨电位动态分布规律不明确，排流与OVPD特性优化难以分析。同时实际回流系统中多类现象仍缺乏理论分析依据，例如线路中多位置OVPD连锁动作情况、钢轨电位异常升高现象等[9]。

针对上述问题，开展城轨回流系统动态排流与钢轨电位控制仿真研究，分析列车动态运行过程中，钢轨电位与杂散电流在排流装置和OVPD动态控制过程中的分布规律，研究多点钢轨电位与杂散电流的耦合作用，为实际系统中OVPD与排流装置的控制优化提供基础。

1 城轨动态排流与钢轨电位控制建模

直流牵引供电系统主要包括牵引变电所、接触网、回流系统、列车，而回流系统包括走行轨、排流网、地网等；为保证回流安全参数在标准允许限值内，回流系统一般在牵引变电所位置设置排流装置与钢轨电位限制装置。带有排流装置与钢轨电位限制装置的直流牵引供电系统示意如图1所示。

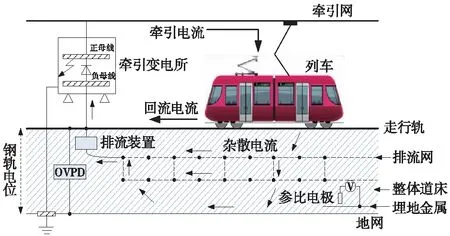
图1 直流牵引供电系统示意

钢轨电位限制装置(OVPD)，可以实时监测钢轨电位，当某一时刻的钢轨电位超过设定值时，钢轨电位限制装置保护合闸，将钢轨与大地短接，降低该位置钢轨电位，从而保护乘客以及工作人员的安全。为实现回流系统钢轨电位保护特性，OVPD主要包括直流接触器和反并联晶闸管，其动作特性如表1所示[10]。

表1 OVPD动作特性

由OVPD动作特性可知，OVPD所在位置轨地等效电阻具有分段特性，其等效电阻公式如下

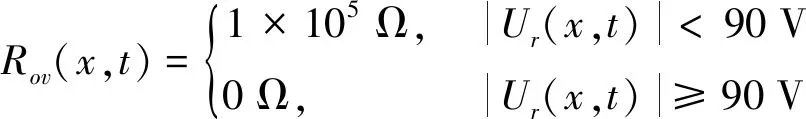
(1)

排流装置[11]，其一端安装在牵引变电所负极，另一端连接排流网与地网，当杂散电流泄露过多，排流装置启动，强制疏导电流进入牵引变电所负极，从而降低杂散电流的危害。

排流装置主要由二极管、限流电阻、IGBT、控制部分和保护部分组成。当结构钢筋极化电位正向偏移值超过 0.5 V，排流装置投入排流，调节排流支路电阻，其支路等效电阻变化具有非线性[12]。本文仿真模型建立及分析时，考虑最大排流情况，排流装置流经电流与两端电压呈线性变化，其等效电阻公式如下

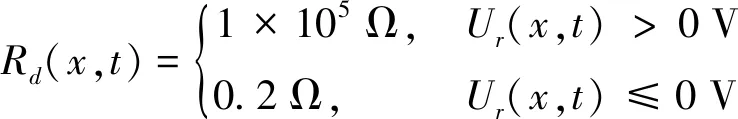
(2)

本文在仿真分析时，以三站两区间为例建立城市轨道交通供电全系统仿真模型，如图2所示。

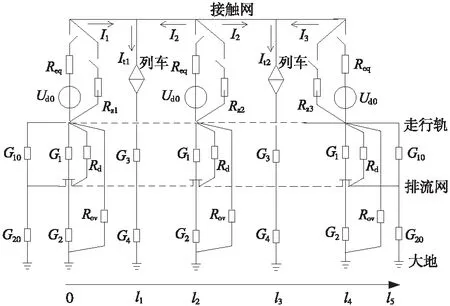
图2 城轨供电全系统仿真模型

在城轨供电系统全模型中，整流机组等效为理想电压源串内阻[13]，其内阻为Req，空载电压为Ud0，整流机组外并内阻Rz可调的再生制动能量吸收装置[14]，I1、I2、I3分别为该时刻牵引变电所1、牵引变电所2和牵引变电所3向列车1和列车2提供的供电电流；列车的功率及位置不断随时间改变，将其等效为时变功率源，It1、It2为列车1与列车2在该时刻的牵引电流。

在“钢轨-排流网-大地”三层结构回流系统中，Rd为排流装置等效电阻，Rov为OVPD等效电阻。R为轨道的单位长度纵向电阻，Gst为单位长度轨道对排流网的电导，Rt为排流网的单位长度纵向电阻，Gtt为单位长度排流网对地电导，牵引变电所、列车位置的走行轨对排流网、排流网对地的集中电导为G1～G4，G10、G20分别是供电区间外线路的轨道对排流网、排流网对地的等效电导[15-16]，i1(x)、i2(x)分别为x位置轨道电流及排流网电流，v1(x)、v2(x)分别为x位置轨道对地电位及排流网对地电位。定义轨道及排流网中电流的正方向与x坐标系的正方向一致。

取全模型回流系统[17-18]其中一个微元分析电压、电流关系，如图3所示。

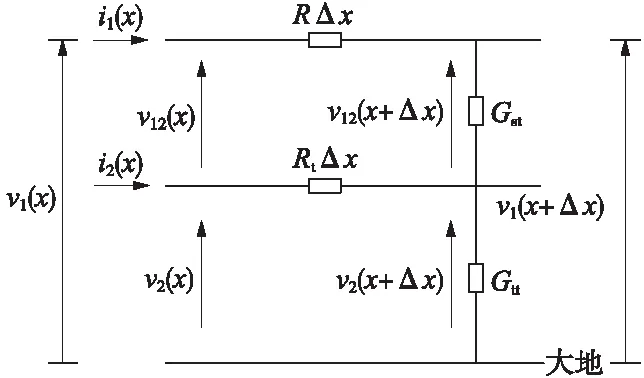
图3 三层结构回流系统微元示意

根据回流系统微元示意图，建立钢轨电位与杂散电流的解析式，如公式(3)所示

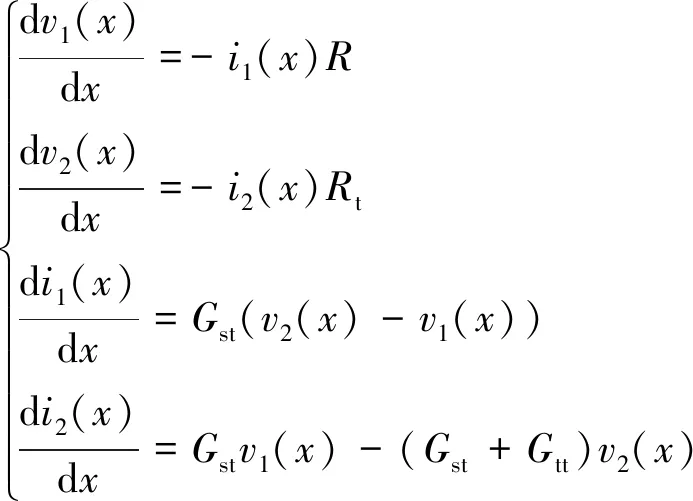
(3)

根据以上方程组求解可得0～l1段钢轨电位与杂散电流的相关参数表达式，如公式(4)～公式(7)所示

v1(x)=C1e-αx+C2eαx+C3e-βx+C4eβx

(4)

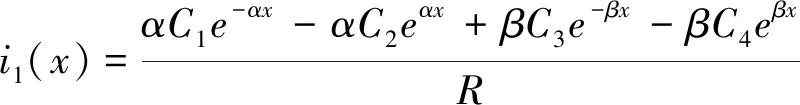
(5)

v2(x)=v1(x)-

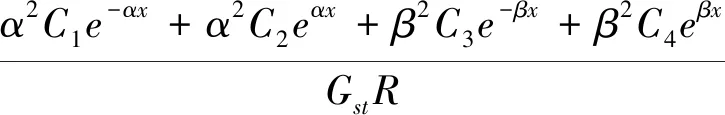
(6)

(7)

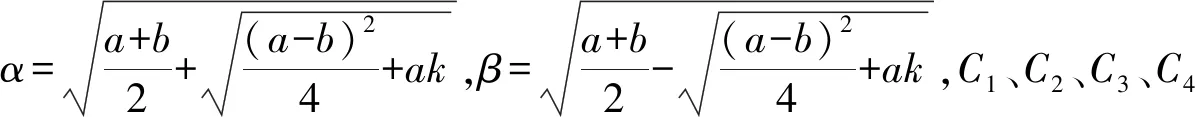
l1～l2、l2～l3、l3～l4段钢轨电位与杂散电流的相关参数表达式与0～l1段相类似，将其通解的待定系数C1、C2、C3、C4对应为C5、C6、C7、C8，C9、C10、C11、C12和C13、C14、C15、C16即可。

为求解上述钢轨电位与杂散电流表达式中的待定系数，需建立边界条件，0～l1、l1～l2、l2～l3、l3～l4段钢轨电位与杂散电流表达式中待定系数共计16个，因此，应建立16个边界条件。

设0～l1、l1～l2、l2～l3、l3～l4段轨道对地电位、排流网对地电位、轨道电流、排流网电流分别为v11(x)、v21(x)、i11(x)、i21(x)；v12(x)、v22(x)、i12(x)、i22(x)；v13(x)、v23(x)、i13(x)、i23(x)；v14(x)、v24(x)、i14(x)、i24(x)。边界条件公式(8)～式(12)如下。

l1位置切面边界条件如公式(8)所示

(8)

l2位置切面边界条件如公式(9)所示

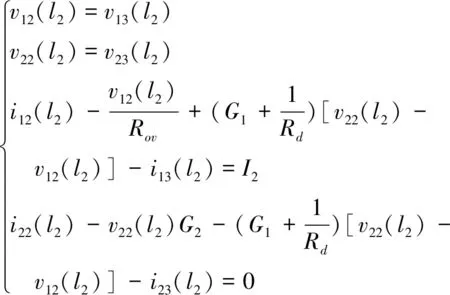
(9)

l3位置切面边界条件如公式(10)所示

(10)

0位置切面边界条件如公式(11)所示

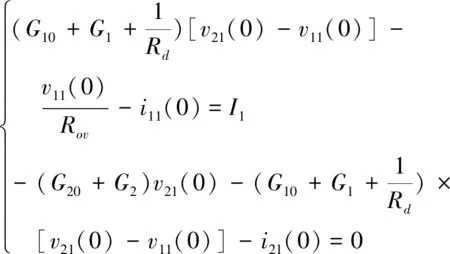
(11)

l4位置切面边界条件如公式(12)所示

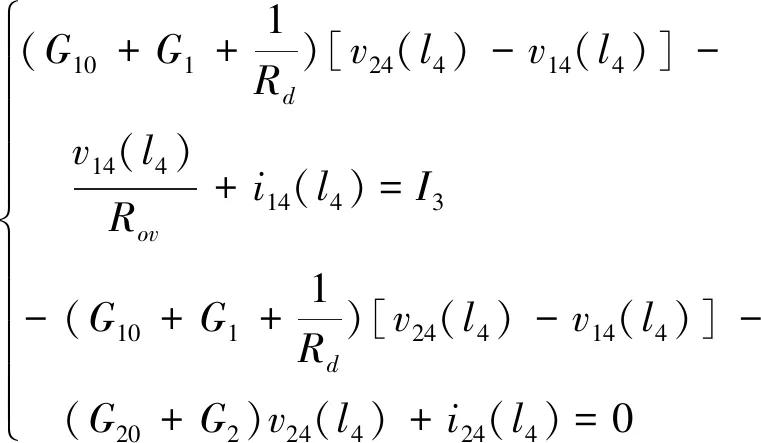
(12)

当|v1(x)|≥90 V时，Rov=0 Ω，|v1(x)|<90 V，Rov=1×105Ω；若v1(x)≤0时，则Rd=0.2 Ω，否则Rd=1×105Ω。

由边界条件公式可以看出，边界条件与它对应时刻的牵引变电所电流和列车牵引电流有关。由于城轨供电系统是复杂的时变系统，所以不同时刻的牵引变电所电流与列车牵引电流是不断变化的，通过列车动态运行特性分析[19]与直流牵引供电系统动态潮流迭代计算[20-21]，可求得列车动态运行过程中，某一时刻、某一位置所对应的牵引变电所电流与流经该列车的电流。所以在排流装置与OVPD投入时，也可求出列车动态运行过程中某一时刻、某一位置的钢轨电位与杂散电流。

2 动态排流与钢轨电位控制仿真

为分析城轨动态排流与钢轨电位控制规律，基于上节建立的动态排流与钢轨电位仿真模型进行仿真分析。仿真过程中，设置三牵引变电所两供电区间的城轨线路，两列车在线路上动态运行，同时分别设置钢轨电位限制装置及排流装置动态控制，分析钢轨电位与杂散电流的动态分布规律。

仿真过程中具体参数设置如表2所示。

表2 仿真参数设置

3个牵引变电所位置分别为0，2，4 km。钢轨电位限制装置和排流装置动作时的电阻特性分别按照公式(1)和公式(2)设置。线路上设置两列车顺序发车，其功率时间特性曲线如图4所示。

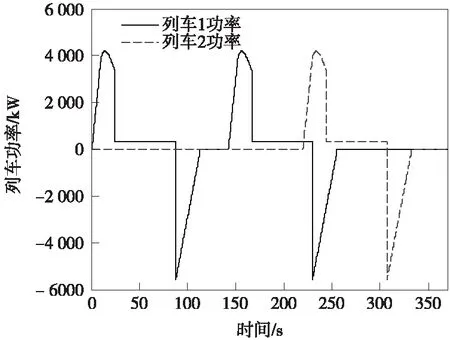
图4 线路列车功率-时间特性曲线

基于上述参数设置，对线路动态运行时排流与钢轨电位控制进行仿真分析。

在排流装置与OVPD均不设置动作时，线路钢轨电位与杂散电流分布如图5所示.

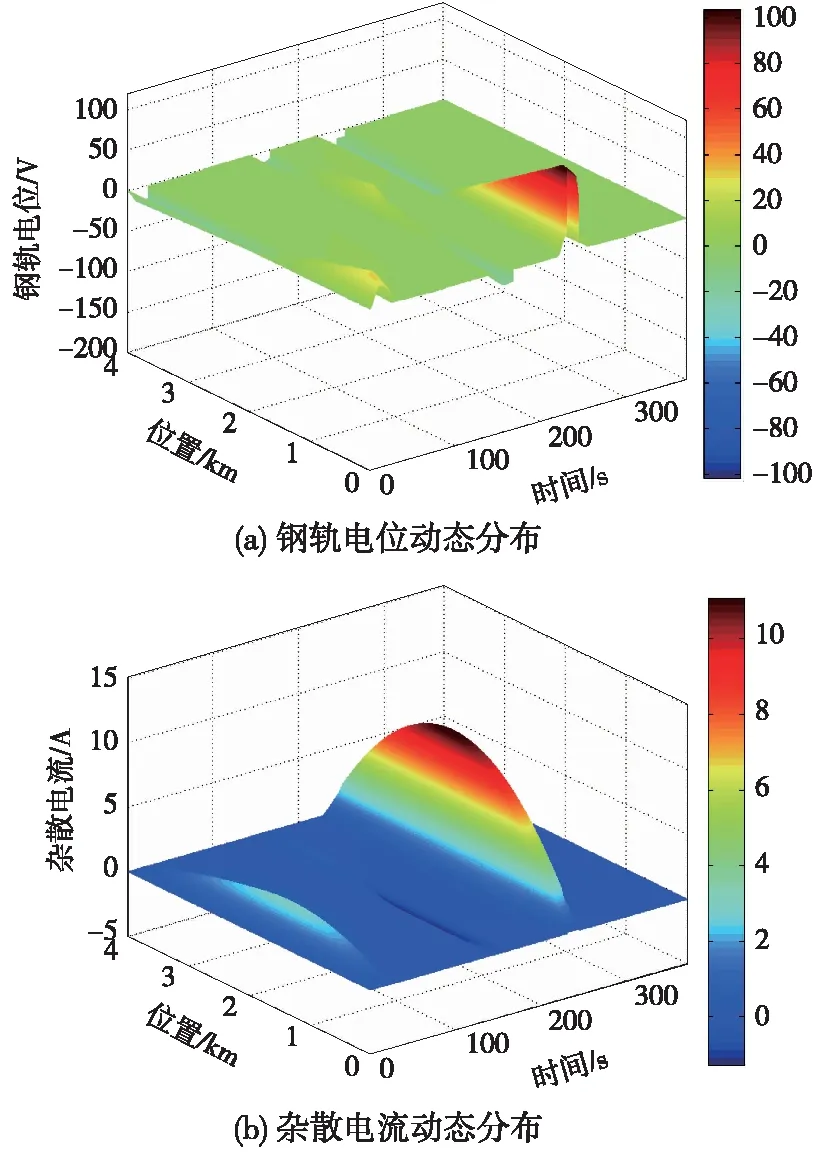
图5 排流柜与OVPD不动作时钢轨电位与杂散电流分布

由仿真结果可知，全线钢轨电位正向最大值为103.5 V，负向最大值为-101.5 V，全线杂散电流最大值为11.1 A。

2.1 钢轨电位控制仿真

设置4 km位置OVPD正常运行，当该位置钢轨电位超过90 V时延时1 s合闸，10 s后分闸。此时全线钢轨电位流动态分布如图6所示。

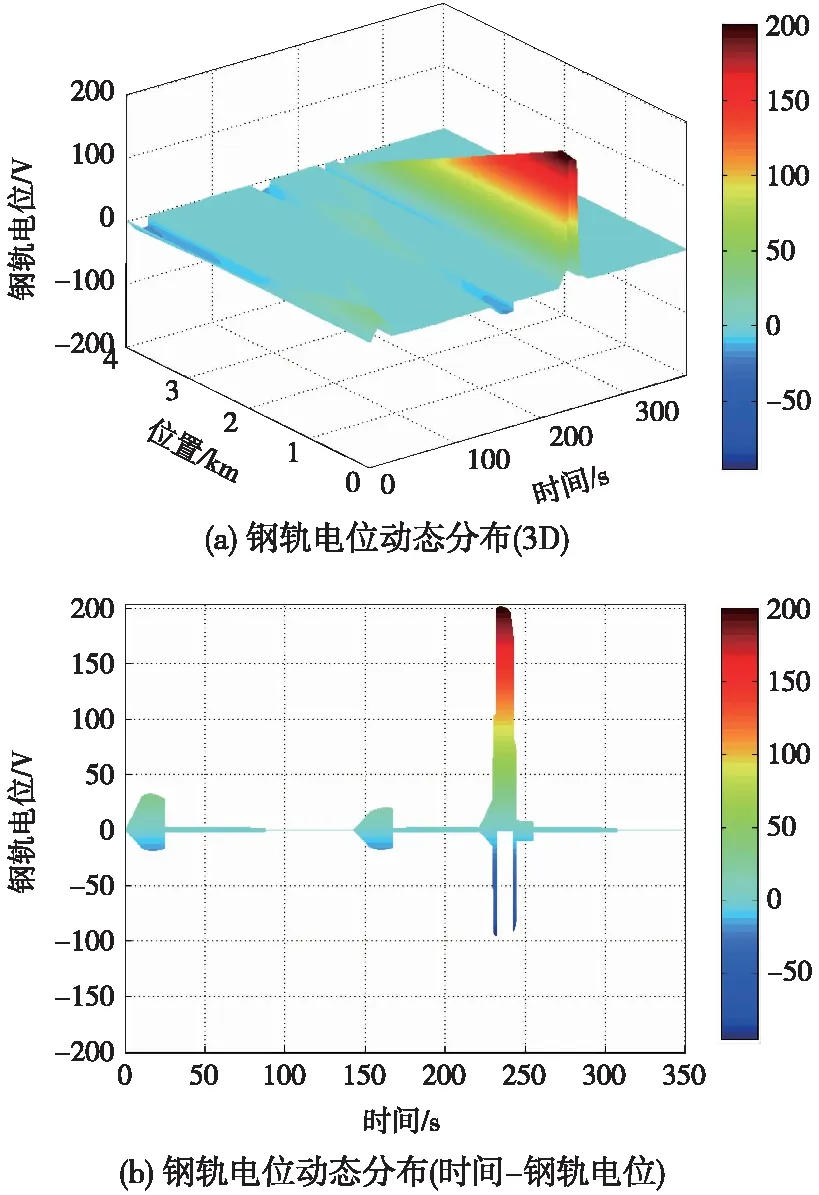
图6 4 km位置OVPD正常动作时钢轨电位分布

当全线OVPD不设置动作时，4 km位置钢轨电位在229.8 s达到-90 V。当设置4 km位置OVPD正常动作时，在230.8 s时刻4 km位置OVPD合闸动作，将轨道与地短接，10 s后OVPD分闸，在此过程中钢轨电位动态分布规律如图6所示。在4 km位置OVPD合闸期间，该位置钢轨电位幅值虽然得到了有效限制，但全线其他位置钢轨电位出现抬升，全线钢轨电位最大幅值达到201.2 V，出现于234.8 s时刻、28 m位置。为进一步分析OVPD动作对全线不同位置钢轨电位的影响，分别对比OVPD动作前后4 km位置、0 km位置钢轨电位随时间的连续变化，如图7所示。在4 km位置OVPD合闸期间，0 km位置钢轨电位相对OVPD不动作期间有了较大幅值的抬升。

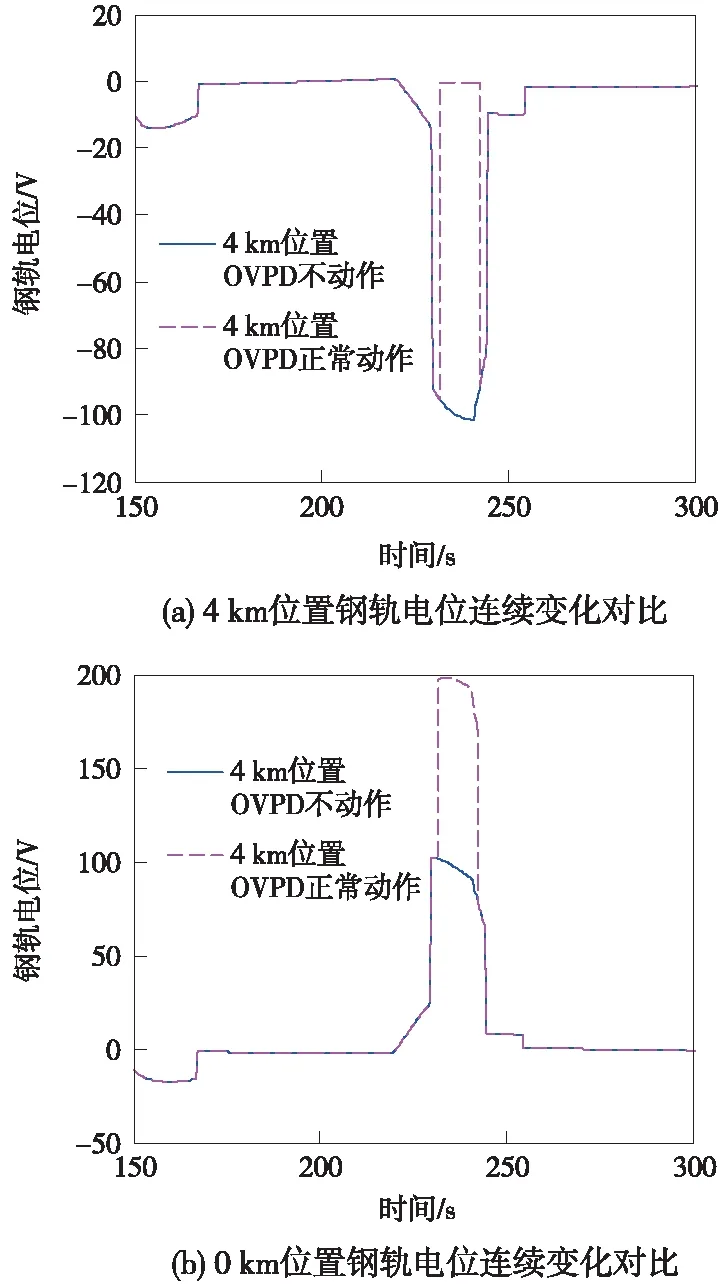
图7 OVPD不同动作情况下钢轨电位对比

OVPD的合闸动作除了会对全线不同位置钢轨电位产生影响之外，对杂散电流的分布影响明显。4 km位置OVPD正常动作时，全线杂散电流动态变化如图8所示。在OVPD不动作时，全线杂散电流最大值为11.1 A。如图8所示，230.8 s至240.8 s期间，由于4 km位置OVPD合闸引起全线杂散电流泄漏量大大增加，最大值可达40.1 A。由此可见，在当前OVPD控制方式下，合闸动作会对全线钢轨电位与杂散电流的动态分布产生较大的影响。

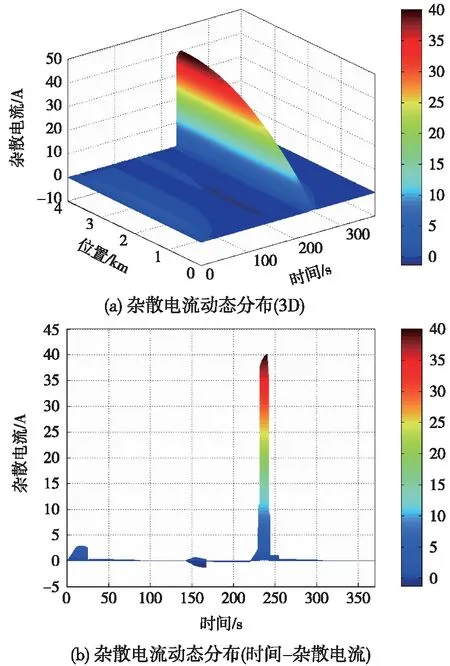
图8 4 km位置OVPD正常动作时杂散电流分布

当全线各牵引变电所位置OVPD均设置正常动作时，全线各位置钢轨电位与杂散电流随时间变化如图9所示。如图9(a)所示，在229.8 s时刻4 km位置的钢轨电位达到90 V，延时1 s后4 km位置牵引变电所的OVPD合闸，此时，导致全线钢轨电位抬升，1 km位置钢轨电位超过90 V后合闸，此后10 s全线钢轨电位被限制在较低水平，正向钢轨电位最大值为35.4 V，负向钢轨电位最大值为32.4 V，10 s后，OVPD分闸。在该过程中，全线杂散电流随时间变化如图9(b)所示，在230.8 s至240.8 s时间段OVPD合闸期间中，全线各位置杂散电流均处于较高水平，杂散电流最大值为259.1 A，远高于OVPD不动作或仅有单个站OVPD动作的情况。由此可见，在钢轨电位控制时，全线各点钢轨电位存在耦合变化情况，某点钢轨电位引起的OVPD合闸可能会导致线路其他位置OVPD连锁动作，该情况在实际线路中发生频繁。同时，多点钢轨电位动作会导致线路杂散电流水平大大增加。

图9 全线OVPD正常动作时钢轨电位与杂散电流分布

2.2 杂散电流排流仿真

设置各牵引变电所位置排流装置正常运行，进行动态排流，分析杂散电流动态排流对系统钢轨电位与杂散电流的影响。

正常排流情况下，系统钢轨电位动态分布如图10所示。由图10可知，系统排流装置按照公式(2)特性进行排流时全线钢轨电位整体抬升，全线钢轨电位最大幅值达到193.7 V，出现于234.4 s时刻、25 m位置。负向钢轨电位幅值减小，线路钢轨电位呈正向偏移，会导致线路杂散电流泄漏水平的增加。而该正向偏移与排流装置动作特性直接相关。

正常排流情况下，系统杂散电流的动态分布如图11所示，系统排流过程导致全线杂散电流水平提升，杂散电流最大值达37.3 A，在4 km位置杂散电流水平最大。

动态排流下钢轨电位与杂散电流分布结果表明，动态排流特性会抬升对全线钢轨电位与杂散电流水平，应通过动态排流特性合理提升来优化系统排流效果。

图10 排流时钢轨电位分布

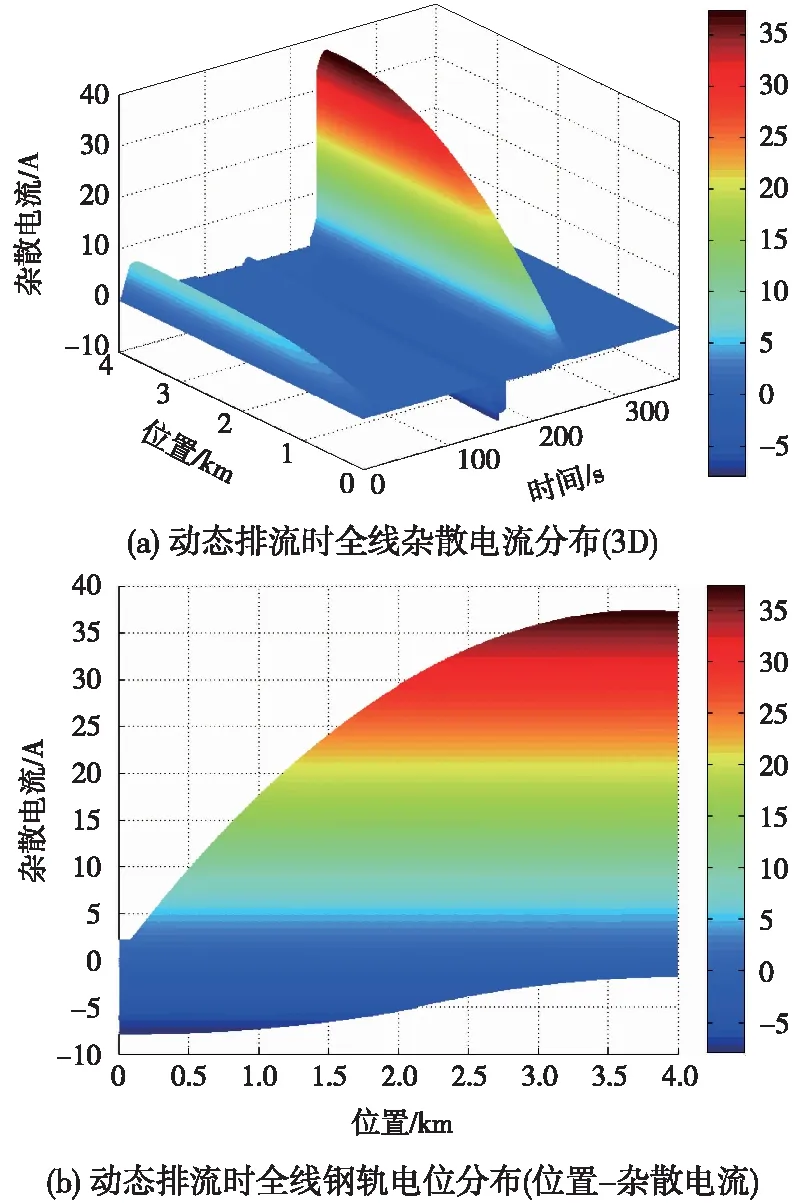
图11 排流时杂散电流分布

3 结语

本文通过建立城轨回流系统动态排流与钢轨电位控制仿真模型，分析了多区间多列车动态运行过程中钢轨电位控制与排流情况下全线钢轨电位、杂散电流分布规律。研究结果表明，单点钢轨电位控制过程中会导致全线钢轨电位分布的动态改变，从而引起其他位置OVPD的连锁动作，此过程中线路杂散电流水平也大大增加。杂散电流动态排流过程中，线路钢轨电位与杂散电流水平均会出现一定程度的抬升。当前系统中钢轨电位控制与杂散电流排流方法应进一步结合系统多点耦合干扰特性进行提升。同时，本文所建立的计及钢轨电位控制与动态排流的仿真模型可为系统OVPD及排流装置动作特性优化提供基础。