虚拟同步发电机对多机系统小干扰稳定性的影响研究
2019-10-11齐志男雷为民孙大卫巨云涛
王 淋,齐志男,雷为民,赵 峰,刘 辉,孙大卫,巨云涛
(1.中国农业大学 信息与电气工程学院,北京 100083;2.国网冀北电力有限公司,北京 100053;3.国网冀北电力科学研究院(华北电力科学研究院有限责任公司),北京 100045;4.国家电网公司风光储并网运行技术实验室,北京 100045)
0 引言
未来电力系统的重要特征之一为高占比的新能源发电形式。以电力电子为并网接口的新能源相比SG(传统同步发电机)具有较低的惯量,对扰动的响应较差。SSG(静止同步发电机)是20 世纪90 年代提出的概念,其原型建立在一种电压可调节的变流器基础上,通过模拟同步机一次调频特性和转子运动惯性,实现与柔性直流输电系统有功和无功功率的动态交互,但SSG 模型忽略了传统SG 励磁系统的调节特性。文献[1-2]通过调节电感中的电流实现虚拟同步机技术,模拟同步机一次电压和频率调节功能,其控制精度受到电感参数的影响。 日本学者提出了电流控制型VSG(虚拟同步发电机)策略[3-4],通过模拟同步机摇摆方程和一次调频特性实现虚拟同步控制,但是该模型只能运行在并网状态。电流控制型VSG自身固有的一些缺点不可避免,故基于电压控制的虚拟同步控制策略应运而生。加拿大学者提出了基于虚拟惯性控制的VSG 技术[5-6],该技术模拟同步机转子运动和一次调频特点,提高了逆变器网侧频率的稳定性,在离网模式下依然能够模拟传统SG 的励磁电压调节特性。英国学者提出一种同步逆变器(synchronveter)控制方法[7-8],通过考虑转子运动惯量和一次调压调频特性,模拟同步机的电磁暂态过程,实现逆变器与发电机在数学模型上的完全等效;但是该模型的无功电压控制环节包含纯积分环节,牺牲了无功响应的快速性。
清华大学[8-12]、华北电力大学[13-14]、合肥工业大学[15-18]、西安交通大学[19-21]和西安理工大学[22-24]等高校也已经相继投入VSG 控制的研究。丁明教授基于同步机电磁暂态模型首次提出VSG模型[10],其主要思路是在VSG 模型中引入电压-频率控制策略,实现变流器的并网和离网之间的自由切换,不过文献中并没有设计VSG 的控制参数,而且控制策略本质上是一种开环控制,准确性与动态性能不够理想。文献[11]给出了一种频率调节的自适应方法,即在电压电流双闭环的VSG 方案下,优化设计VSG 控制器的参数实现离并网之间的无缝切换。文献[22]增加了虚拟同步机模拟SG 模型的阶数,以使得VSG 更准确地模拟同步机特性。文献[23]给出了VSG 并网预同步控制策略,该方案采用闭环控制虚拟功率,使VSG 输出电压与网侧电压相位保持一致,并利用二次调压调频,使电压幅值和频率达到并网要求。文献[24]建立了与虚拟同步机并联的有功-频率控制的小信号模型,利用根轨迹法研究了虚拟阻尼和虚拟转动惯量对VSG 出力的影响。
文献[25]针对VSG 输出瞬时无功功率中脉动量对电压的不利影响,建立了小信号模型优化控制参数并分析其对系统的影响,提出利用截止频率和相角裕度来设计VSG 参数,能够满足系统的动态性能,最后研制小型三相并网逆变器进行试验。文献[26]通过对VSG 控制和下垂控制进行小信号建模分析,比较2 种控制方式的动态响应,利用状态空间模型研究振荡现象,实验结果表明VSG 控制完全继承了下垂控制的优点,并为系统提供了惯量支撑。文献[27]设计了具有和SG 相应特性相同的VSG 控制器,对其虚拟励磁、惯性时间常数等参数建立线性化数学模型,分析上述参数变化给VSG 带来的影响。文献[28]建立VSG 工频小信号模型,证明了在一定条件下有功环和无功环可以近似解耦,因此其控制参数可独立设计。文献[29-30]建立VSG 功频调节环的小信号模型,对转动惯量的影响进行分析,设计出根据频率变化可自动调节的转动惯量控制方案,可避免频率的骤然升降。文献[31-32]建立了频率50 Hz 下的VSG 小信号模型,对有功和无功功率环的参数进行分析和设计,得出阻尼影响功频调节环的开环增益。
国内外的研究大多基于VSG 模型的研究,尤其是VSG 控制参数对VSG 的影响,然而对于VSG 大规模接入多机电力系统后对系统小干扰稳定性的影响研究不足。本文主要研究内容是建立含VSG 的多机电力系统线性化模型,利用特征值法研究不同出力占比、不同位置及不同参数下VSG 对多机系统区间联络线低频振荡的影响。
1 VSG 的数学模型
电压型VSG 的动态方程为:

式中:H 为惯量常数,H=6 kg/m2;D 为阻尼系数,取D=0;Pm和Pe分别为机械功率和电磁功率;δ为转子角度;ω 为转子角速度;ω0为角速度基值,ω0=2πf0。
VSG 模型框图如图1 所示,其中s 为拉普拉斯算子。
电压型VSG 控制部分采用有功功率和无功功率控制策略,无功功率-电压控制方程为:

式中:Efd为控制电压;Qref为无功功率参考值;Q为无功功率;Kq为无功功率控制系数,Kq=0.001;E0为电压,E0=0.001 p.u.。
无功功率-电压控制框图如图2 所示。

图1 电压型VSG 基本框图
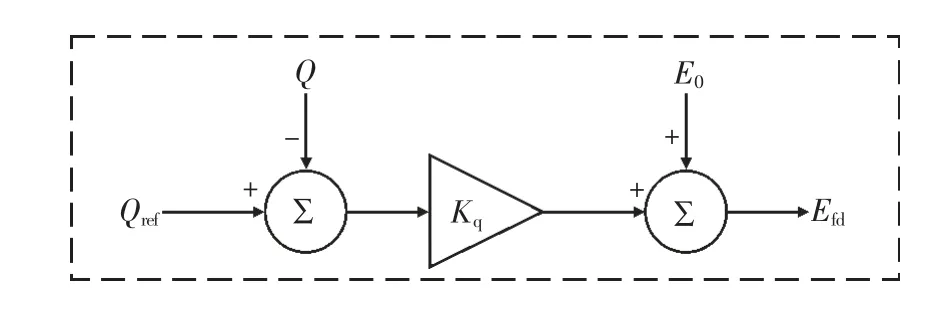
图2 VSG 无功功率-电压控制框图
有功功率-频率控制方程为:
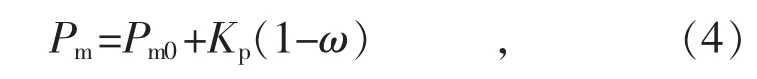
式中:Kp为有功功率控制系数,Kp=0.001;Pm0为机械功率初始值。平衡节点时,Pm0为任意值;非平衡节点时,Pm0=0.000 22 p.u.。
有功功率-频率控制框图如图3 所示。


VSG 功率方程为:

式中:ud,uq,id和iq分别为电压和电流的d 轴、q轴分量。
VSG 并网接口方程为:
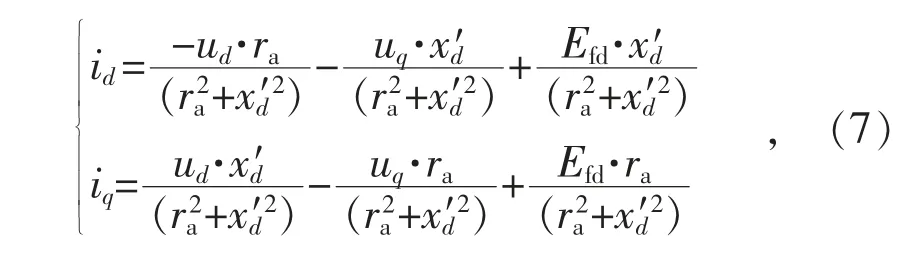
式中:ra为VSG 电阻,ra=0.002 2 p.u.;为虚拟暂态电抗,=0.3 p.u.。
电流实部、虚部与d 轴、q 轴分量之间的转换关系为:
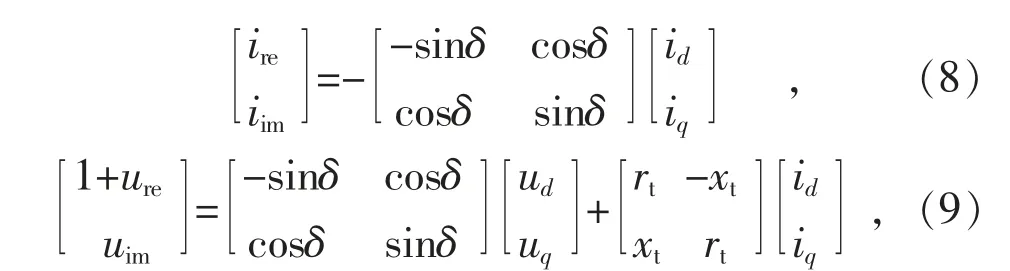
式中:ure,uim,ire,iim分别为电压和电流的实部和虚部分量;rt和xt为升压变压器电阻和电抗。
VSG 发出电压的幅值和相角为:
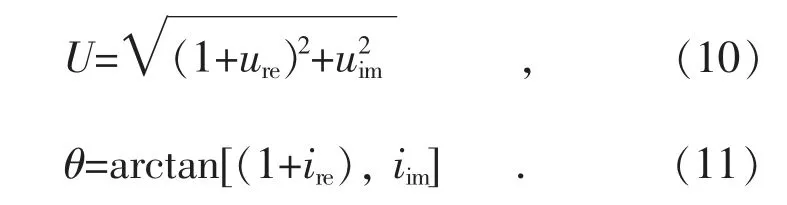
VSG 发出(定义为负)的有功功率Pg和无功功率Qg用电压和电流的实部与虚部表示为:

2 VSG 和SG 小信号模型
(1)VSG 小信号模型

式中:XVSG和AVSG分别为VSG 状态变量和状态矩阵;BVSG,CVSG和DVSG为VSG 并网系统的代数矩阵;ΔωVSG和ΔδVSG分别为VSG 的角速度和相角偏差;ΔV1和Δθ1分别为与VSG 相连的同步机端口电压的幅值和相角偏差。
VSG 与多机系统的有功和无功功率变化量ΔP 和ΔQ 分别为:

其中,
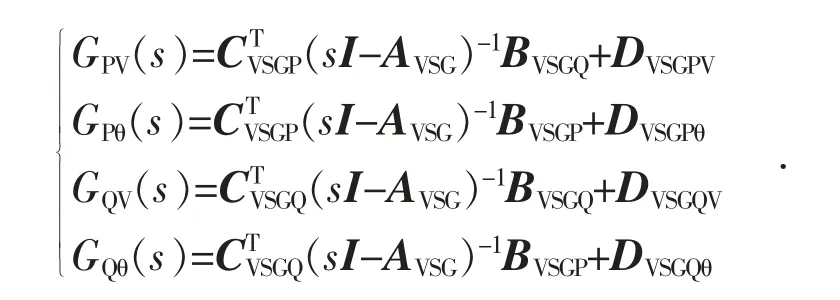
(2)SG 小信号模型

式中:

式中:δi,ωi和zi分别为第i 台SG 的转子角度、角速度和其他状态变量;ΔXSG为SG 的状态变量;ΔASG为SG 的状态矩阵;b,c 和d 为构成SG 及线路参数的代数矩阵。
由上述同步机状态空间方程可得四机两区域系统的传递函数形式为:
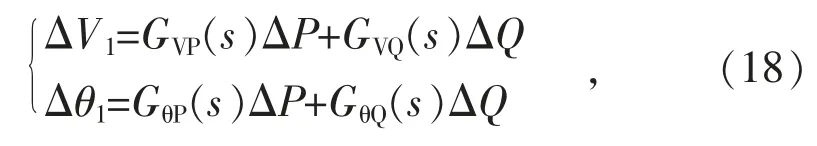
其中,

3 仿真分析
四机两区域系统结构如图4 所示,在该系统中220 kV 联络线连接2 个相似区域。功率潮流从左侧区域流向右侧区域。2 个区域各自含有2台额定电压都是20 kV 的SG。G1,G2 和G4 为有功出力均为700 MW 的PV 节点,G3 为有功功率为719 MW 的平衡节点,负荷均通过节点7 和9进行功率传输。

图4 四机两区域系统结构
全是SG 时的区间振荡模式见表1。

表1 全是SG 时的区间低频振荡模式
3.1 虚拟转动惯量H 的影响
表2—4 分别为虚拟转动惯量H 为0.5,3 和6 时VSG 不同出力占比及接入位置的振荡模式,图5—7 分别为不同H 对应的时域仿真结果。
从表2—4 可以看出,VSG 接在受端与全是SG 时相比,区间联络线输出有功功率的阻尼比变小,振荡频率增大。VSG 出力占比提高,阻尼比变大(小于全是SG 时),振荡频率变小。VSG 接在送端时振荡频率减小,阻尼比小于全是SG 时,但好于VSG 接在受端的情况。
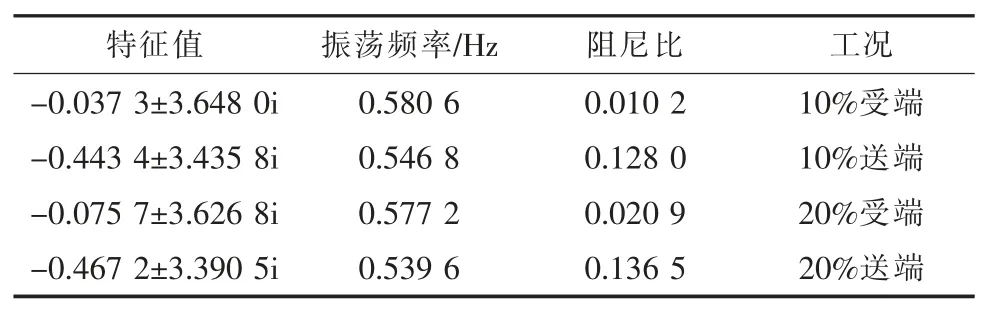
表2 H=0.5 kg·m2 时的区间联络线典型振荡模式

表3 H=3 kg·m2 时的区间联络线典型振荡模式

图5 H=0.5 kg·m2 时VSG 在受端和送端的联络线有功振荡

图6 H=3 kg·m2 时VSG 在受端和送端的联络线有功振荡

表4 H=6 kg·m2 时的区间联络线典型振荡模式

图7 H=6 kg·m2 时VSG 在受端和送端的联络线有功振荡
虚拟转动惯量H 提高,其对区间低频振荡的支撑增强。随着H 的增大,VSG 接在受端时阻尼比增大(小于全是SG 时),振荡频率减小(刚开始大于而后小于全是SG 时);VSG 接在送端时阻尼比几乎不变,振荡频率减小(均小于全是SG 时)。
3.2 虚拟阻尼系数D 的影响
表5—7 分别为虚拟阻尼系数D 取0.5,3 和6 时区间联络线的振荡模式,其时域仿真结果如图8—10 所示。

表5 D=0.5 时的区间联络线典型振荡模式

图8 D=0.5 时VSG 在受端和送端的联络线有功振荡
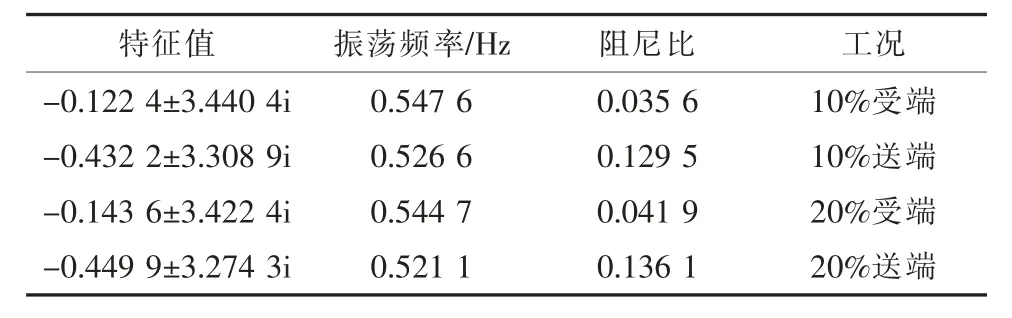
表6 D=3 时的区间联络线典型振荡模式
从表5—7 可以看出,VSG 接在受端与全是SG 时相比,区间联络线输出有功功率的阻尼比和振荡频率变小,随着VSG 出力占比提高,阻尼比变大,振荡频率变小。VSG 接在送端时振荡频率减小,阻尼比小于全是SG 时,但好于VSG 接在受端的情况。

图9 D=3 时VSG 在受端和送端的联络线有功振荡

表7 D=6 时的区间联络线典型振荡模式
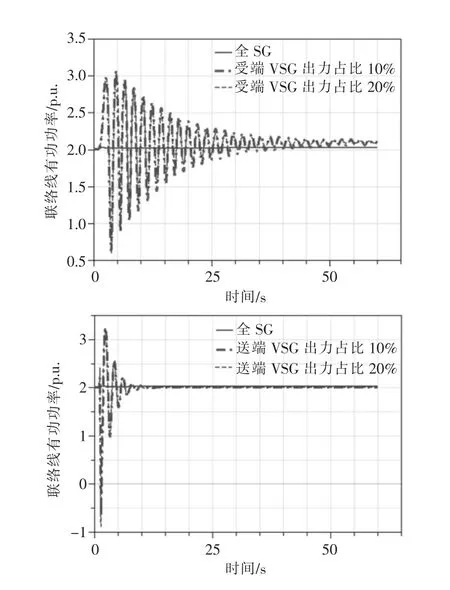
图10 D=6 时VSG 在受端和送端的联络线有功振荡
随着虚拟阻尼系数D 增大,阻尼低频振荡的效果变好。D 增大,VSG 接在受端时联络线低频振荡功率振荡对应的阻尼比和振荡频率都会增加(均小于全是SG 时);VSG 接在送端时,阻尼比增大,振荡频率却几乎不变。
3.3 无功功率控制系数Kq 的影响
表8 和表9 分别为无功控制系数Kq取0.000 5和0.002 时的区间联络线振荡模式,其时域仿真结果如图11 和图12 所示。

表8 Kq=0.000 5 时的区间联络线典型振荡模式

图11 Kq=0.000 5 时VSG 在受端和送端的联络线有功振荡

表9 Kq=0.002 时的区间联络线典型振荡模式
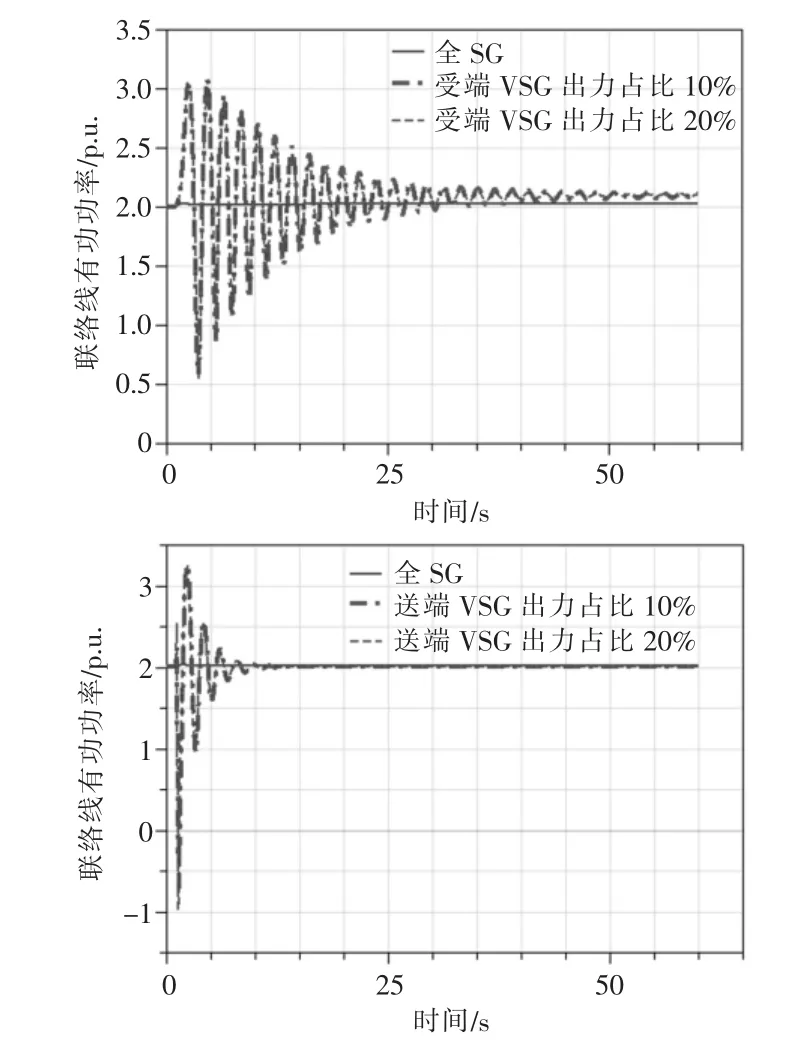
图12 Kq=0.002 时VSG 在受端和送端的联络线有功振荡
从表8 和表9 可以看出,VSG 接在受端与全是SG 时相比,区间联络线输出有功功率的阻尼比变小,振荡频率略微增大。VSG 出力占比提高,区间联络线低频功率振荡阻尼比增大,振荡频率减小。VSG 接在送端时振荡频率略微减小,阻尼比小于全是SG 时,但好于VSG 接在受端的情况。
随着无功功率控制系数Kq增大,其对系统电压支撑能力变强,因此VSG 接在2 个区域内时区间联络线低频振荡的阻尼比均有所增大。
3.4 有功功率控制系数Kp 的影响
表10 和表11 分别为无功控制系数Kp取0.000 5 和0.002 时的区间联络线振荡模式,其时域仿真结果如图13 和图14 所示。
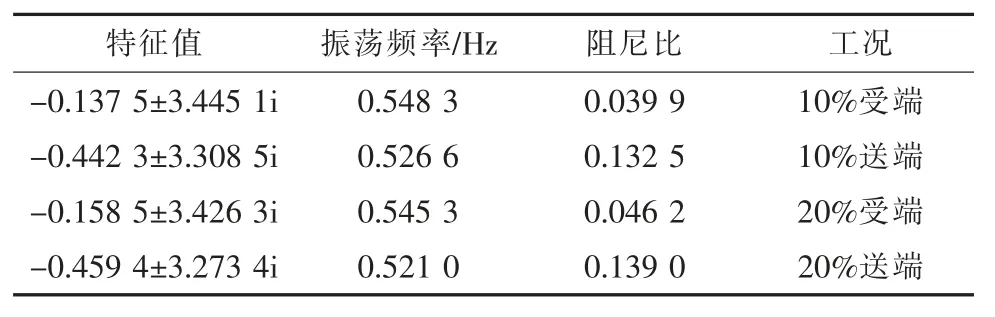
表10 Kp=0.000 5 时的区间联络线典型振荡模式
从表10 和表11 可以看出VSG 接在受端与全是SG 时相比,区间联络线输出有功功率的阻尼比和振荡频率变小。随着VSG 出力占比提高阻尼比增大,振荡频率减小。VSG 接在送端时振荡频率减小,阻尼比小于全是SG 时,但是好于VSG 接在受端的情况。
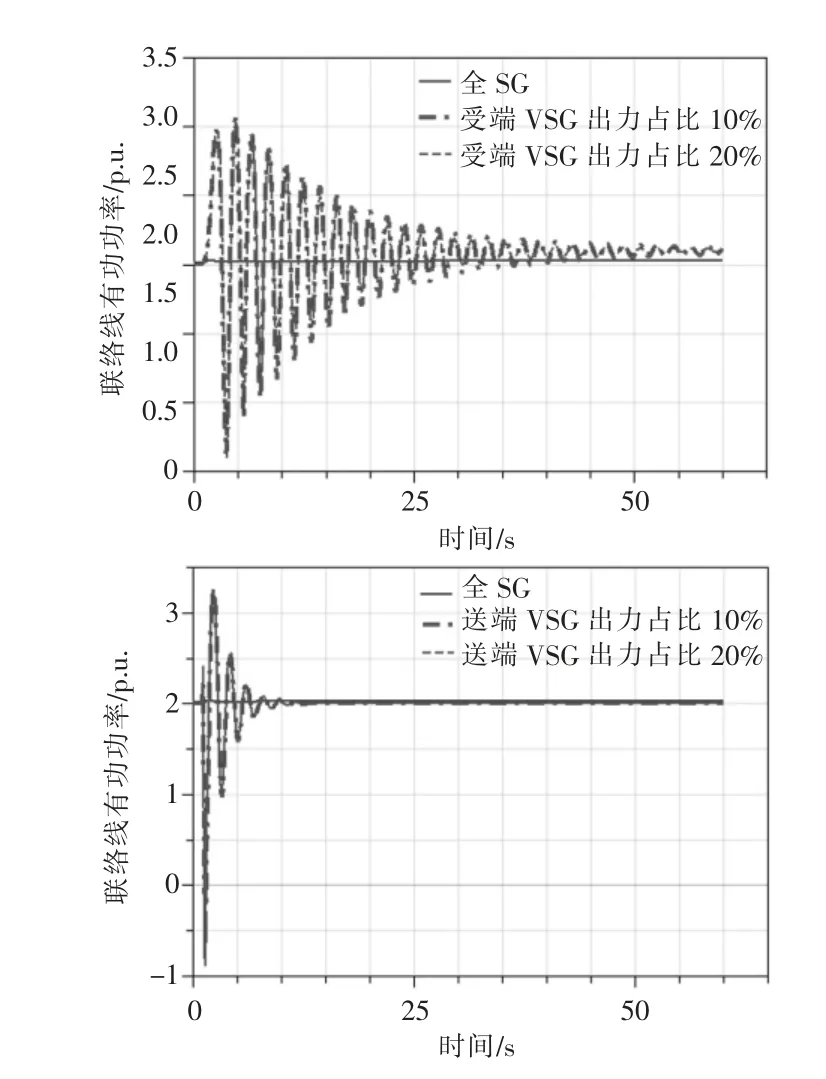
图13 Kp=0.000 5 时VSG 在受端和送端的联络线有功振荡
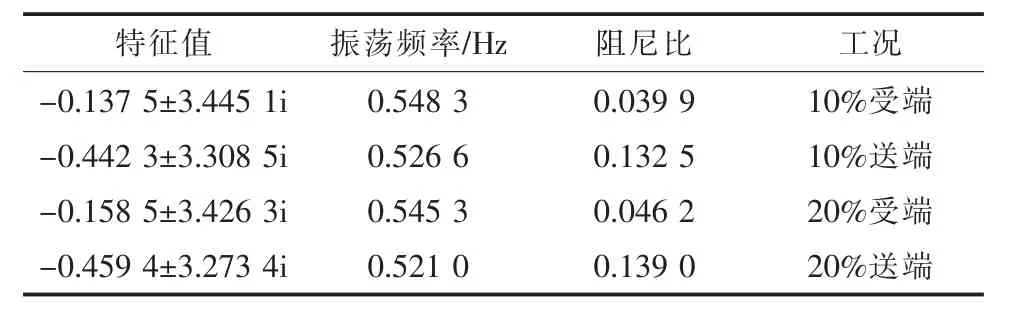
表11 Kp=0.002 时的区间联络线典型振荡模式

图14 Kp=0.002 时VSG 在受端和送端的联络线有功振荡
对比发现有功功率控制系数Kp的改变对于VSG 接在不同区域对区间联络线低频振荡的影响甚微。
4 结论
本文通过搭建含VSG 的四机两区域系统,研究了VSG 接入后对多机系统区间联络线低频功率振荡的影响,得到结论如下:
(1)随着VSG 出力占比的提高,区间联络线低频功率振荡阻尼比变大,振荡频率变小。
(2)VSG 的接入减小了区间联络线低频振荡对应的阻尼比,且VSG 接在受端时影响更大,因此在工程实际中建议将VSG 接入潮流的送端。
(3)不同参数下VSG 对多机系统小干扰稳定性有以下影响:
虚拟转动惯量H 增加,使得VSG 接在受端时阻尼比增大,振荡频率减小;使得VSG 接在送端时阻尼比几乎不变,振荡频率减小。
随着虚拟阻尼系数D 增大,VSG 接在受端时区间低频振荡的阻尼比和频率都会增加;VSG 接在送端时区间低频振荡的阻尼比增大,频率几乎不变。
无功控制系数Kq增大,VSG 接在受端时区间低频振荡阻尼比增大,频率下降;VSG 接在送端时阻尼比增大,振荡频率几乎不变。
有功控制系数Kp的变化对于VSG 对区间低频振荡的影响很小。
