基于ProMPs和PI2的机器人学习方法
2019-10-11申思远
傅 剑,曹 策,申思远
(武汉理工大学自动化学院,湖北 武汉,430070)
近年来,示范学习结合强化学习框架已成功应用于机器人运动技能的获取,但如何基于示范任务学习让机器人快速获得完成新任务的能力仍然是个难题。运动基元是一种用于表示机器人运动策略的方法,可以看作是组成各种复杂运动的基本结构单元,能产生机器人新的运动状态、调节运动速度、进行多任务协作以及学习示范轨迹等。常见的运动基元模型有基于时间索引的DMPs[1-2]和基于状态索引的SEDs[3],这两种模型都是确定状态下的动力系统模型,其完成多任务的能力有限,而且基于传统运动基元模型的机器人学习方法存在学习速度慢、学习结果精度低等问题。概率运动基元(probabilistic movement primitives, ProMPs)[4-6]是一种非动力系统模型,它表达的是机器人运动轨迹的分布概率,此轨迹可以定义在关节空间、笛卡尔空间或者其他任意空间上,其中关节空间上的轨迹分布是本研究关注重点。
在实际的机器人系统中,任何动作都存在观测和执行的噪声,因此,为了获得更好的学习效果,本文提出一种新的机器人学习方法。首先使用ProMPs模型在多条示范轨迹中找到一条概率最大的轨迹进行模仿学习[7-9],然后在这一条轨迹的基础上运用贝叶斯估计算法[10]进行新任务学习,并在完成任务的基础上加入路径积分PI2(Policy Improvement with Path Integrals)策略[11]进行轨迹搜索,在设置的约束条件下找到一条最优轨迹。最后,通过协作机器人UR5实验平台并结合机器人仿真软件V-REP,以经过标记点为任务,与传统融合DMPs-LWR[2]和PI2策略的运动技能获取方法进行对比实验,来验证本文方法的可行性和有效性。
1 概率运动基元ProMPs
1.1 概率运动基元表示
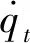
(1)
(2)
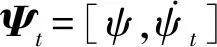
显然,一条观测轨迹的概率可表达为:
(3)
假设有M条示范轨迹,通过基函数的线性拟合可以得到M组权值:W={ω1,…,ωm,…,ωM}。
不失一般性,定义ω服从参数为θ的概率分布:
ω~p(ω;θ)=N(ω|μω,Σω)
(4)
将式(4)代入式(3),可得:
(5)
参数θ={μω,Σω}可以从多条示范轨迹中通过最大似然法获得,计算方法如下:
(6)
将由式(6)得到的参数θ={μω,Σω}代入式(5),可以很容易估计出任意时间点的均值和方差。
1.2 相变量和时间的关系
本文引入相变量z来将运动和时间解耦。相变量可以是关于时间的任意增函数,通过改变相变量来调节运动速度。这里使用的相变量函数如式(7)所示,相变量和时间的关系曲线见图1。
(7)
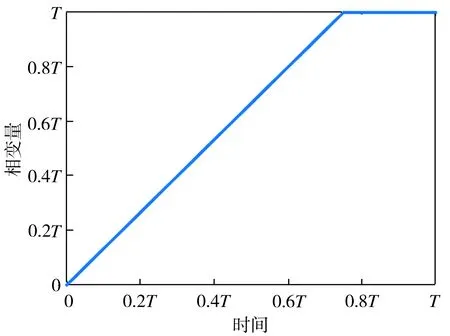
图1 相变量和时间的关系曲线
式(7)中,斜率4/3可以保证相变量是关于时间的增函数,且在3T/4时刻,机器人基本平稳到达终点。在实际应用中可以根据情况调整此斜率值。确定了相变量之后,就可直接使用相空间中的基函数来代替时域里的基函数。
1.3 基函数
本文采用高斯基函数:
(8)
式中:h表示每个基的宽度;ci表示第i个基的中心。
对基函数进行归一化,得:
(9)
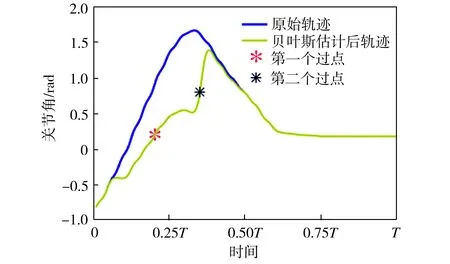
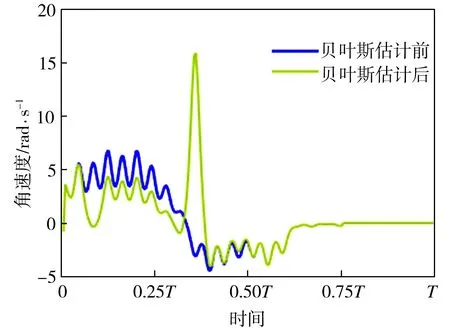
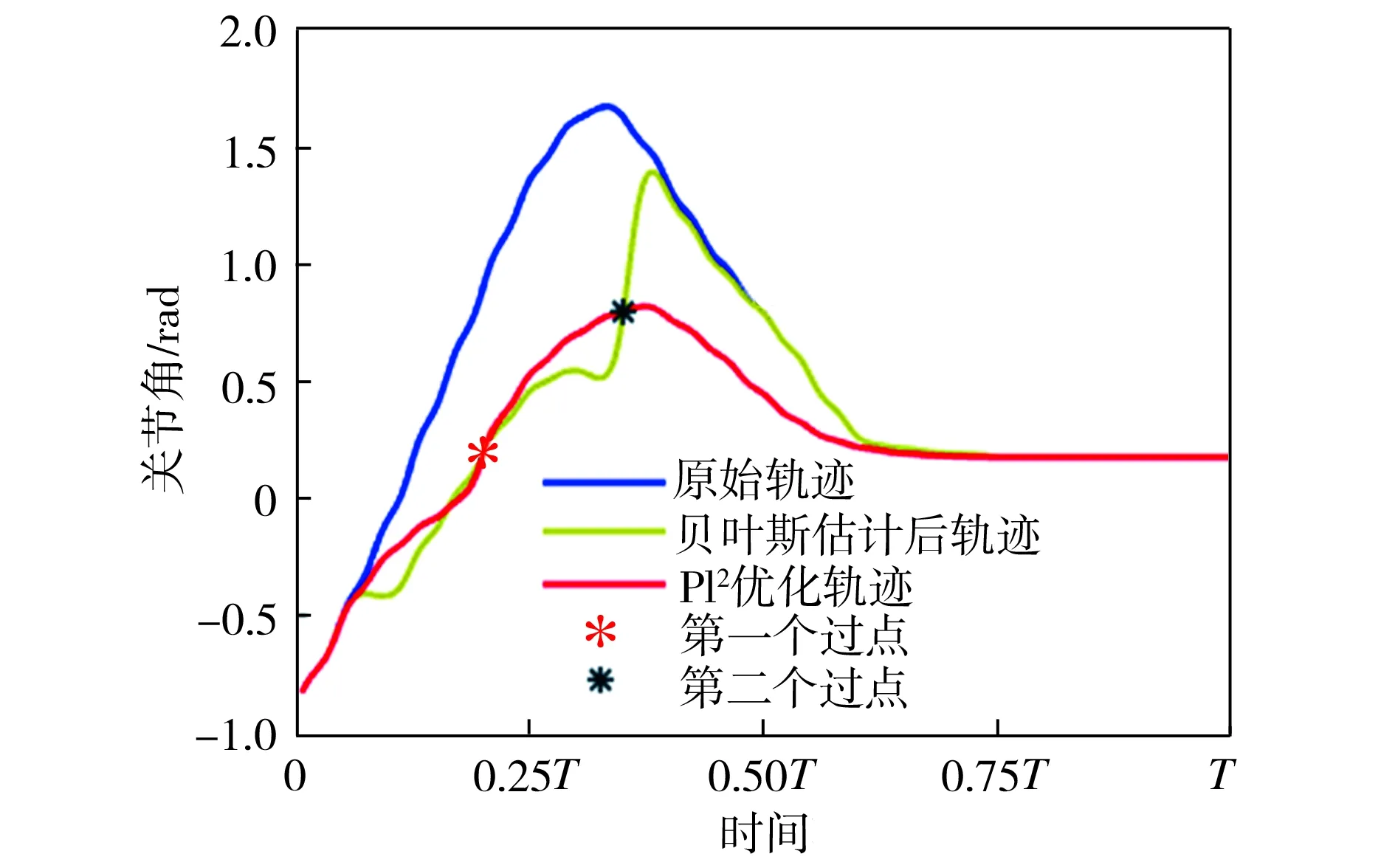
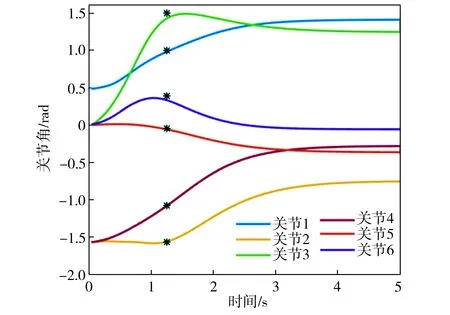
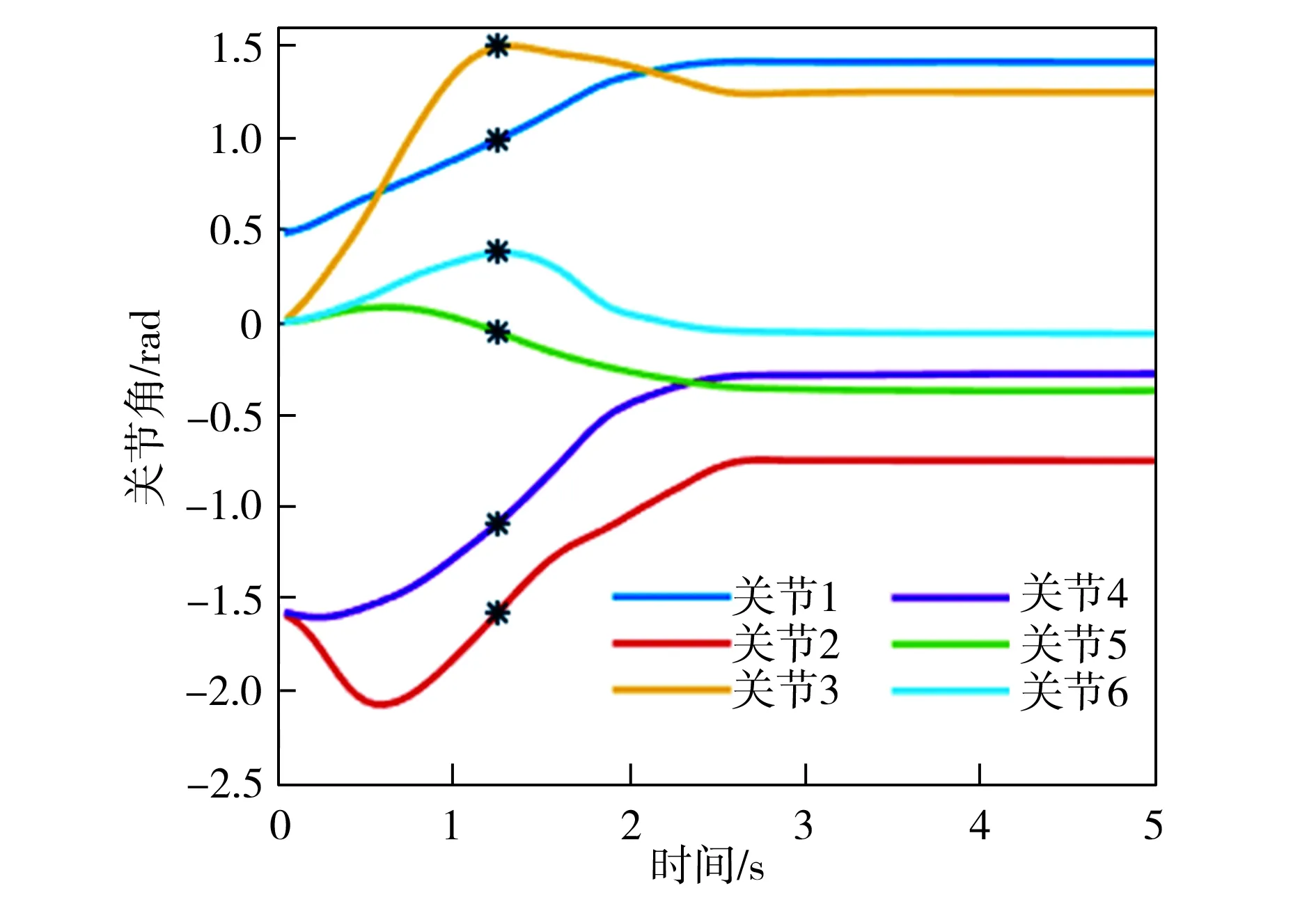
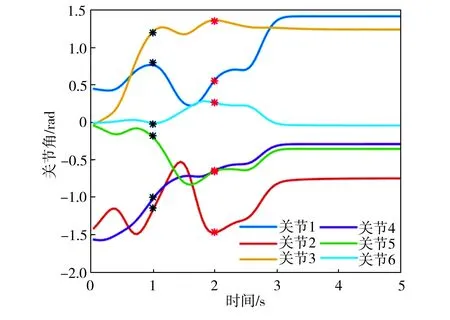
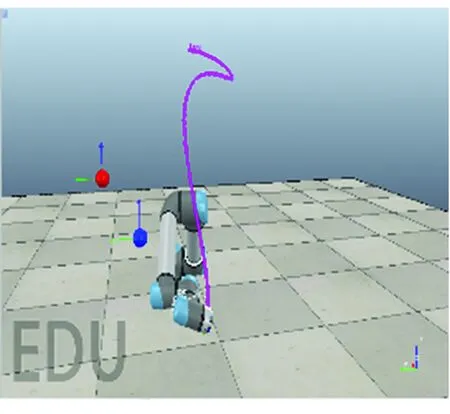
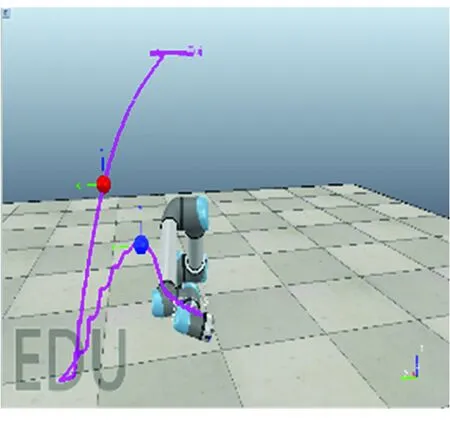
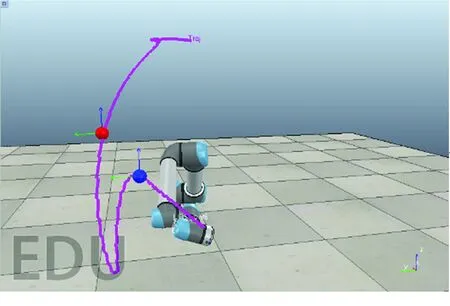
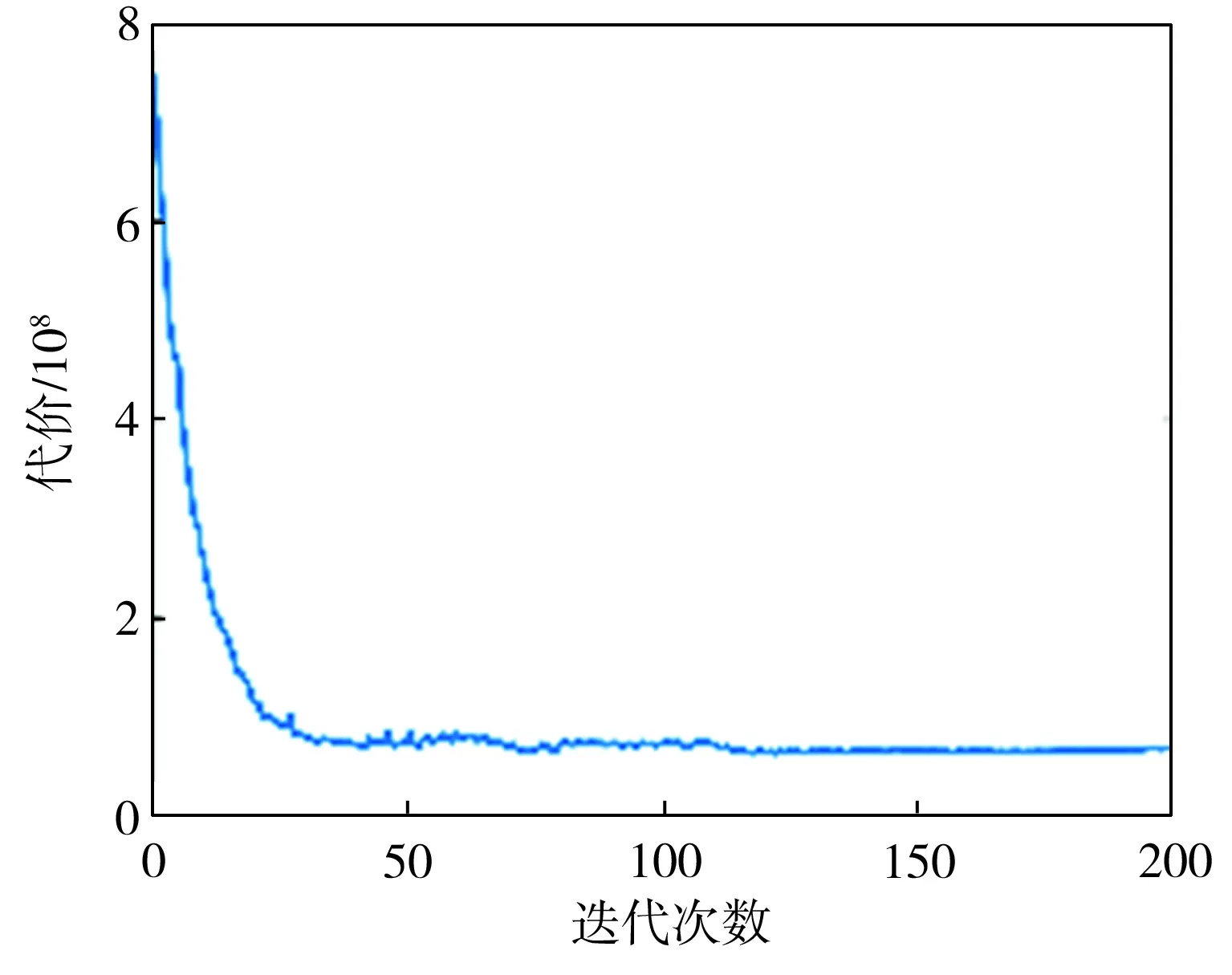
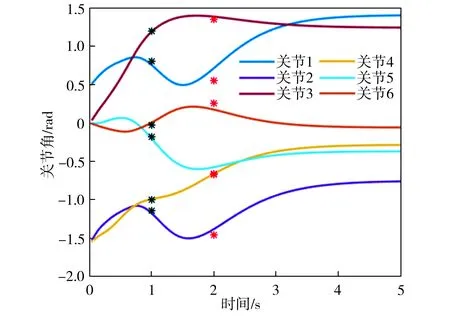
基函数归一化可以增强函数拟合的效果。如图2所示,归一化后,基函数的中心均匀分布在[-δ,T+δ]区间上,其中0<δ 图2 基函数分布 (10) (11) (12) 将更新后的参数θ+代入式(5),即可得到新的轨迹概率。本文使用此概率公式产生一条新的轨迹,从而实现过点任务,如图3所示。图3中蓝色的线是机器人模仿学习到的示范轨迹,设置点一位置(0.2T,0.2 rad)和点二位置(0.35T,0.8 rad),经过贝叶斯估计之后获得黄色轨迹。从图3可以看出,经过贝叶斯估计更新参数之后,机器人可快速达到预期的过点效果,但与此同时,更新后的轨迹并不平滑。 图3 通过贝叶斯估计获得的轨迹 图3中各条轨迹的运动速度如图4所示。从图4中可以明显看出,经过贝叶斯估计更新之后的轨迹速度在0.6T前变化起伏较大。图3和图4说明,贝叶斯估计方法可以使机器人获得良好的运动精度,但是会损失运动的平稳性。 图4 贝叶斯估计前后的轨迹运动速度 Fig.4 Comparison of trajectory speeds before and after Bayesian estimation 如上所述,通过对原始轨迹进行贝叶斯估计实现了快速精准的过点,ProMPs和相变量的使用保证机器人最终能平稳到达预定位置。但是在实际应用中,机器人轨迹规划往往还有很多其他的优化目标,比如满足关节约束条件、力矩或运动能量最小、轨迹足够平滑等,这时就需要利用路径积分PI2策略,让机器人进一步学习和改善技能。 PI2是一种结合最优控制和动态规划的强化学习算法。具体来说,对于一个随机动态系统,为进行最优控制,可以根据贝尔曼最优准则和随机HJB(Hamilton-Jacobi-Bellman)方程,得到一个线性偏微分方程形式的优化目标函数,然后利用费曼-卡茨定理就可以把要解决的随机最优控制问题近似地转换成路径积分问题,从而间接地得到目标值函数的解。 需要指出的是,本文使用的是PI2改进型。它利用核典型相关分析(KCCA)提取机器人关节间的非线性相关性,并作为一种启发式信息对PI2施加摄动ε,从而提高PI2的收敛速度。该方法由本课题组提出,在文献[12]中有详细描述。使用ProMPs可以让机器人很好地学习到示范轨迹,式(1)中的ω就是学习到的权值,通过蒙特卡洛模拟实验对权值加入随机摄动(ω+ε),产生K条变分路径,从而得到K条代价不同的路径,然后对其进行加权平均处理,并进行权值更新。这个过程中的最优控制量为: (13) (14) (15) 式中:λ为常系数;S(τti,k)为第k条轨迹的代价函数;εti,k为第k个样本第i时刻的摄动值。 P(τi,k)是用各个轨迹的代价通过Softmax函数映射到区间[0,1]得到的概率来表示的,由式(14)可知,代价越高的轨迹其概率反而越小,从而保证了PI2向代价低的地方收敛。本文第k条轨迹的代价函数公式如下: (16) (17) (18) 然后,在上述代价函数中加入过点的惩罚项: (19) 最终,第j个关节第k个权系数的第l个分量的PI2更新公式如下: (20) (21) 式(20)是对权值增量在各个时间点进行加权平均。式(20~21)中:Δωi;j是第j个关节在第i时刻的最佳权系数(控制值),Δωi;j;k;l为其第k个权系数的第l个分量;Bi;j;k;l为Bi;j的第k个权系数的第l个分量,其中Bi;j对应于第j个关节在第i时刻的基函数;N为运动终点时刻索引值。 综上所述,基于贝叶斯估计和KCCA启发式PI2策略优化算法的核心是,通过ProMPs对机器人轨迹进行模仿学习,然后使用贝叶斯估计和PI2进行取长补短:一方面,贝叶斯估计会导致轨迹过于曲折,但是其优点是过点简单快速(即迅速获得新任务的可行解),这一特性对于机器人的实时控制意义重大;另一方面,单独使用PI2策略搜索会相对比较耗费时间且学习能力有限,但是能够让机器人学习到平滑、完美的轨迹(附加泛函指标约束)。贝叶斯估计和PI2两者相互结合就实现了轨迹快速、平稳、精准过点。 经过PI2学习后的轨迹如图5中红线所示,可以看出该轨迹明显平滑了很多。同时,学习过程只经过了几十次迭代就可以收敛,而单独使用PI2完成过点任务时至少需要几百次学习,并且仅向指定点靠近,无法实现过点。 图5 PI2学习前后的轨迹对比 Fig.5 Comparison of trajectories before and after PI2learning 下面将利用机器人仿真软件V-REP和协作机器人UR5来验证本文算法。UR5有6个关节,易于编程,高度可定制化,很适合于过点实验任务。实验流程如下:首先采用ProMPs从多条示范轨迹中学习参数θ={μω,Σω},然后采用贝叶斯估计算法重新规划出一条轨迹,使之通过随机设置的点,最后利用PI2在参数空间进行策略搜索,完成平滑轨迹过点任务。此外,为了进行对比分析,还采用了传统的DMP-LWR-PI2[2,11]学习策略完成相同的任务。 该实验中根据式(10~12)计算在过点任务要求下的新任务轨迹。首先设定轨迹的起点和终点,然后利用UR5的最小能量运动模式生成示范轨迹,其中6条曲线对应6个关节,最后设置过单点任务,通过不同学习策略优化方法来完成。图6为LWR-PI2学习后的轨迹,图7为贝叶斯ProMPs-PI2学习后的轨迹。从图6~图7可以看出,采用本文算法可以精准地通过标记点,轨迹也较平滑,而采用LWR-PI2方法时关节3和关节6都有一定的误差。 图6 LWR-PI2学习后的过单点运动轨迹 图7 贝叶斯ProMPs-PI2学习后的过单点运动轨迹 Fig.7 Trajectories via one point learned by Bayesian ProMPs-PI2 图8和图9为UR5的实验照片,其中红色标志物是设置的过点任务,图8对应于图6中LWR-PI2学习后的UR5笛卡尔空间轨迹,图9对应于图7中贝叶斯ProMPs-PI2学习后的空间轨迹。从图8~图9中可以看出,LWR-PI2所学轨迹仅仅是擦过标志物,但经过贝叶斯ProMPs-PI2优化后,UR5能快速精准地经过标记点,从而可完成击中、拾取等任务。 Fig.9 Image of UR5 trajectory learned by Bayesian ProMPs-PI2 为进一步验证贝叶斯估计的快速过点能力和PI2的优化能力,下面进行过两点任务实验,采用与过单点任务时相同的示范轨迹。首先,单独运用贝叶斯估计获得如图10所示轨迹。从图10中可以看出,即使是复杂的6关节过两点任务,采用贝叶斯估计算法也可以精准完成。 图10 贝叶斯估计学习后的过两点轨迹 Fig.10 Trajectories via two points learned by Bayesian estimation 在机器人仿真软件V-REP中得到的过两点轨迹如图11所示。从图11可以看出,轨迹经过了设置的两个球形标志物,但是轨迹并不平滑。 (a)示范轨迹 (b) 贝叶斯估计学习轨迹 Fig.11 Trajectory via two points learned by Bayesian estimation in V-REP simulation 通过PI2策略搜索优化后,可以得到如图12所示的各关节轨迹,V-REP中的机器人仿真轨迹如图13所示。相比于图11(b),图13中机器人运动轨迹平滑了很多,这证明了PI2优化策略的有效性。 图12 贝叶斯ProMPs-PI2学习后的过两点轨迹 Fig.12 Trajectories via two points learned by Bayesian ProMPs-PI2 图13 V-REP仿真中贝叶斯ProMPs-PI2学习后的过两点轨迹 Fig.13 Trajectory via two points learned by Bayesian ProMPs-PI2in V-REP simulation PI2优化过程中的代价函数值变化如图14所示,该指标包括过点惩罚项和曲线平滑项。由图14可见,随着迭代的进行,代价函数值迅速下降,经过120次迭代后基本稳定,这表明PI2算法调整了轨迹的平滑度并最终达到收敛。 图14 PI2优化过程中的代价值变化 图15所示为机器人某关节的速度在优化前后的对比。从图15可以看出,优化后关节角速度变化范围比优化前的小很多,进一步佐证了前面的研究结论。 图15 PI2优化前后的关节速度对比 Fig.15 Comparison of joint velocities before and after PI2optimization 图16为采用LWR-PI2学习策略的过两点实验结果,其过点时间和过点位置要求都与采用其他学习策略时相同。从图16可以看出,机器人无法完成所要求的任务。 图16 LWR-PI2学习后的过两点轨迹 综上所述,贝叶斯ProMPs可以实现快速过点,而PI2强化学习方法可以优化贝叶斯估计方法获得的不平滑轨迹,减少轨迹的能量消耗,两者取长补短。 本文提出的贝叶斯ProMPs-PI2机器人学习策略将贝叶斯估计应用于ProMPs模型,并加入启发式的KCCA-PI2方法优化轨迹,不仅可以快速完成所要求的过点任务,还能找到一条平滑且能量消耗较小的优化路径。通过UR5的过单点及过两点任务实验,证明采用该方法能快速而精准地完成从示范任务到陌生任务(本文为过点任务)的泛化学习,从而实现机器人的新技能获取。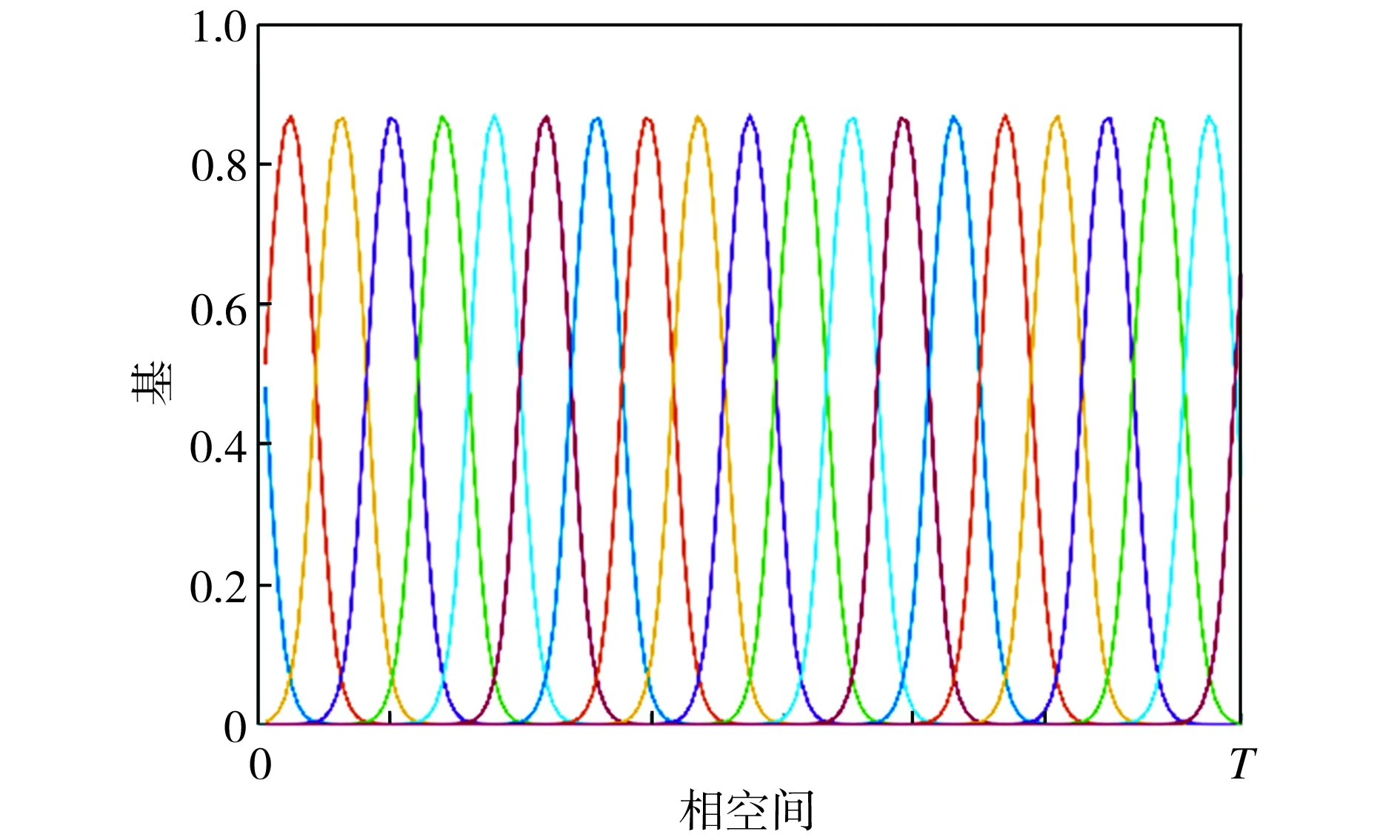
2 贝叶斯估计算法
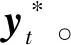
3 基于贝叶斯ProMPs-PI2的策略优化算法
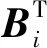

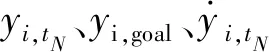


4 实验及结果分析
4.1 过单点任务
4.2 过两点任务


5 结语
