一个包含完全数的非线性Euler函数方程的解

申江红，高 丽，张明丽

(延安大学 数学与计算机科学学院，陕西 延安 716000)

如果一个数恰好等于它的因子之和，则称该数为完全数，第一个完全数是6，第二个完全数是28。对于Euler函数φ(n)方程解的研究一直以来都是数论方向的重要领域之一，对于形如

φ(ab)=k(φ(a)+φ(b))

(1)

的Euler函数φ(n)的线性方程有着一定的研究。文献[1]讨论了k为素数时的情况，给出了k=3时的部分解；文献[2]给出了k=3时方程(1)的全部解；文献[3]给出了k=4时方程(1)的全部解；文献[4]给出了k=4,6时方程(1)的全部解；文献[5]给出了k=5时方程(1)的全部解；文献[6]给出了k=7时方程(1)的全部解；文献[7]给出了k=8时方程(1)的全部解；文献[8]给出了k=9时方程(1)的全部解。

本文将讨论一个包含完全数的非线性Euler函数方程：

φ(mn)=φ(m)+28φ(n)+28

(2)

的解，并给出其全部34组解。

1 定理及其证明

定理方程(2)有解：(m，n)=(196，3)，(294，3)，(37，15)，(37，16)，(37，20)，(37，24)，(37，30)，(57，16)，(57，20)，(63，16)，(63，20)，(74，15)，(76，15)，(44，10)，(50，8)，(50，12)，(66，8)，(66，10)，(58，4)，(58，6)(33，39)，(33，45)，(33，72)，(33，78)，(33，84)，(33，90)，(66，39)，(66，45)，(44，8)，(44，12)，(29，87)，(29，116)，(29，174)，(58，87)。

证明设gcd(m,n)=d，则φ(d)=m1φ(d)，

φ(n)=n1φ(d)，其中m1,n1∈Z+。由方程

φ(d)(dm1n1-m1-28n1)=28，从而有

φ(d)=1，2，4，14，28。

情况1φ(d)=1。

此时有dm1n1-m1-28n1=28，由φ(d)=1，可得d=1,2。

当d=1时，有m1n1-m1-28n1=28，从而有(m1-28)(n1-1)=56。根据因式与因数所有可能的关系，建立关系式从而得到：

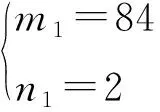
当d=2时，有2m1n1-m1-28n1=28，从而有

(m1-14)(2n1-1)=42，因而有

情况2φ(d)=2。

此时有dm1n1-m1-28n1=14，由φ(d)=2，可得d=3,4,6。

当d=3时，有3m1n1-m1-28n1=14，从而有

(3m1-28)(3n1-1)=70，因而有

此时gcd(m,n)≠3，从而方程(2)无解。

此时gcd(m,n)≠3，从而方程(2)无解。

当d=4时，4m1n1-m1-28n1=14，从而有

(m1-7)(4n1-1)=21，因而有

此时gcd(m,n)≠4，从而方程(2)无解。

当d=6时,6m1n1-m1-28n1=14，从而有(3m1-14)(6n1-1)=56，不存在m1,n1∈Z+使得其情况成立，此时方程(2)无解。

情况3φ(d)=4。

此时有dm1n1-m1-28n1=7，由φ(d)=4，可得d=5，8，10，12。

当d=5时，有5m1n1-m1-28n1=7，从而有

n1φ(d)=8，则m=29，58；n=15，16，20，24，30。此时gcd(m,n)≠5，从而方程(2)无解。

当d=8时，8m1n1-m1-28n1=7，从而有

n1φ(d)=4，则m=25，33，44，50，66；n=5，8，10，12。此时gcd(m,n)≠8，从而方程(2)无解。

当d=10时，10m1n1-m1-28n1=7，从而有

n1φ(d)=20，则m=13，21，26，28，36，42；n=25，33，44，50，66。此时gcd(m,n)≠10，从而方程(2)无解。

当d=12时，12m1n1-m1-28n1=7，从而有(3m1-7)(12n1-1)=28，不存在m1,n1∈Z+使得其情况成立，此时方程(2)无解。

情况4φ(d)=14。

此时有dm1n1-m1-28n1=2，由φ(d)=14，可得d无解，从而方程(2)无解。

情况5φ(d)=28。

此时有dm1n1-m1-28n1=1，由φ(d)=28，可得d=29,58。

当d=29时，有29m1n1-m1-28n1=1，从而有

n1φ(d)=56，则m=29，58；n=87，116，174，从而方程(2)有解(m，n)=(29，87)，(29，116)，(29，174)，(58，87)。

当d=58时，58m1n1-m1-28n1=1，从而有(29m1-14)(58n1-1)=43，不存在m1,n1∈Z+使得其情况成立，此时方程(2)无解。

2 结语

Euler函数φ(n)是数论中的一类极其重要的函数，有关此类方程的解的研究也是数论方向的活跃课题之一。本文给出了一个包含完全数的非线性Euler函数φ(n)的方程φ(mn)=φ(m)+28φ(n)+28的全部34组解。