蜂窝夹层板强度分析模型对比研究

苏 玲，刘 赛，尹 进，肖 凯

(中国运载火箭技术研究院，北京 100076)

0 引言

蜂窝夹层板与金属板、普通复合材料层合板相比，具有高比刚度、高比强度的特点，广泛应用在飞行器结构设计中。蜂窝夹层板一般由上下面板和夹芯组成，需要建立等效强度校核模型，以降低计算成本，提高计算效率。因此，蜂窝夹层板的力学等效方法成为一个重要的研究课题。

在早期的研究中，通常把蜂窝夹层板简化为等刚度的板，具有代表性的有Allen理论[1]、Reissner理论[2]、Hoff理论[3]等，每种理论基于不同的假设条件。随着计算机技术和有限元计算方法的发展，可以进一步减少对蜂窝夹层板的受力假设。但由于蜂窝夹层结构复杂的细节结构特点，目前工程上仍然不采用详细模型对其进行强度校核，一般采用简化的三明治夹芯板模型和实体三明治夹芯板模型。然而各种等效理论以及工程等效模型都有其适用范围和计算精度，需要对此深入了解，才能应用这些方法进行飞行器结构强度设计。

本文分别采用计算精度较高的Hoff理论[4]、在工程中广泛采用的三明治夹芯板模型和实体三明治夹芯板模型对蜂窝夹芯板的强度进行了计算，并以详细的蜂窝体夹芯板模型为基准，对不同模型的计算结果进行了比对分析并得到相应结论。

1 强度校核模型

1.1 Hoff等效板模型

Hoff理论中，设定蜂窝夹层板满足以下假设条件：1)中厚度面板假设，认为面板同时具有面内刚度和弯曲刚度；2)认为夹芯不承受面内应力，不具有面内刚度；3)忽略夹芯和面板的法向应力分量，假定法向应力为零。

等效板理论是将整体蜂窝夹层板等效为不同厚度的各向同性材料板。等效板强度模型的优点是易于计算。等效板为弯曲板，满足小挠度薄板的Kirchhoff假设。

在Hoff理论中，由蜂窝夹层板的刚度公式和弯曲板的刚度公式得到蜂窝夹层板的等效参数[5]:

等效厚度为

(1)

等效弹性模量为

(2)

等效泊松比为

μeq=μf

(3)

等效密度为

(4)

式(1)～式(4)中，hf为面板厚度，hc为夹芯高度，Ef为面板弹性模量，μf为面板泊松比，ρc为夹芯密度,ρf为面板密度,k为考虑胶膜等附加质量的系数，通常k取1.3～2.1。

计算完成后，由等效板的应力计算得到蜂窝夹层板上下面板的应力[5]，计算过程如下：

由板弯理论和蜂窝芯子不承受面内载荷的假设得到内力矩应力σM为

(5)

平面内应力σN为

(6)

σup=σM-σN，σlower=σM+σN

(7)

式(7)中，σup为上面板应力，σlower为下面板应力。

1.2 三明治夹芯板模型

三明治夹芯板模型将整体蜂窝夹层板假设为层合板，分为3部分:第1部分为上面板铺层；第2部分将蜂窝芯等效为正交各向异性材料，作为层合板的一层铺层；第3部分为下面板铺层。各部分厚度为各铺层的真实厚度，蜂窝芯等效性能计算公式为[6]

(8)

式(8)中，γ为修正系数，理论值取1，一般取0.4～0.6,Es、Gs、ρs、μs分别为芯子材料的弹性模量、剪切模量、密度和泊松比,t为蜂窝芯子壁厚，l为蜂窝外接圆半径。

1.3 三明治实体夹芯板模型

三明治实体夹芯板模型将蜂窝芯子等效为六面体单元，上下面板分别通过壳单元建模，与六面体单元共结点连接。六面体单元赋予等效的各向异性材料性能[7]：

G33=Ecc，G55=Gcyz，G66=Gcxz，即压缩模量及两个方向的剪切模量。其他Gij为0，为防止数值运算溢出，G11=G22=G44=min(G33,G55,G66)×0.001。

需要说明的是，为了得到更准确的计算结果，在芯子厚度方向通常划分多个单元。

1.4 蜂窝体夹芯板模型

蜂窝体夹芯板模型对蜂窝夹芯板进行了详细的建模，具体到对蜂窝芯格详细建模，蜂窝芯格与上下面板共结点连接。各部分材料性能赋予真实材料性能。

2 研究算例

本文对一块长768mm、宽443mm、高30mm的铝蜂窝夹层板进行了等效方法研究，计算该板的应力、变形及频率响应。夹层板面板和夹芯选材均为铝，各方法计算过程中所用材料性能如表1所示。夹芯为六边形蜂窝，芯格边长为4mm，芯格厚度为0.05mm。

表1 铝材料性能

该夹层板的边界条件及加载方式如图1所示，一边固支，另一边均匀加载。点1为应力取值点，点2为位移取值点，点1和点2位于夹层板y向长度中点。

图1 算例平板边界条件及加载方式Fig.1 The boundary and loading mode of the example plate

3 计算结果对比研究

以蜂窝体夹芯板模型为基准，对4种计算模型下的蜂窝夹芯板频率、变形和应力结果进行了对比分析。4种计算模型采用有限元分析模型，图2为4种计算模型示意图。

表2～表5分别为4种计算模型下的蜂窝夹芯板频率、变形和应力结果，同时列出了以蜂窝体夹芯板模型为基准的各计算结果误差。

(a) Hoff等效板模型

(b) 三明治夹芯板模型

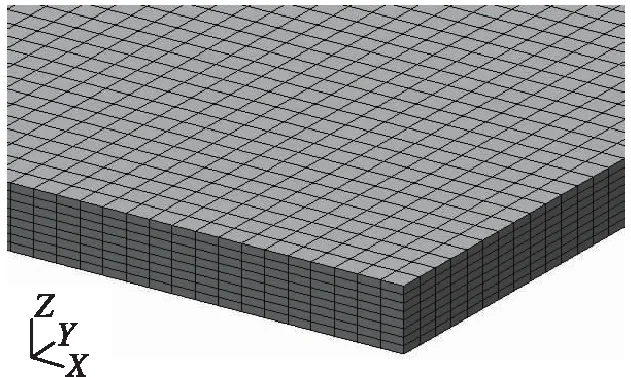
(c) 三明治夹芯板实体模型

(d) 蜂窝体夹芯板模型

频率Hoff等效板模型/Hz误差三明治夹芯板模型/Hz误差三明治夹芯板实体模型/Hz误差蜂窝体夹芯板模型/Hz1阶39.565-33.14%54.242-8.34%53.481-9.63%59.1782阶146.31-29.36%175.97-15.04%172.81-16.57%207.133阶243.06-30.69%294.54-16.01%289.81-17.36%350.67

表4 变形分析结果及误差

表5 应力分析结果及误差

由表2可以看到，Hoff等效板模型的频率分析结果小于基准，误差在-34%以内。两种三明治夹芯板模型的频率分析结果相当，均小于基准值，误差在-18%以内。

由表3可以看到，3种模型第1阶振型均为法向弯曲，第2阶振型均为x向扭转弯曲，第3阶振型均为法向弯曲。

由表4分析结果得知，3种模型位移分析结果均大于基准值，误差在9%以内。

由表5分析结果得知，3种模型上下表面的X向应力均大于基准值，其中，Hoff等效板模型误差在142%以内，两种三明治模型的计算结果相当，误差在36% 以内。3种模型上下表面的Y向均小于基准值，其中Hoff等效板模型误差在-4%以内，两种三明治模型的计算结果相当，误差在-50%以内。

4 芯子材料等效性能计算界面

在工程结构设计过程中，芯子材料弹性性能数据通常需要通过等效计算得到，尤其是蜂窝夹芯弹性性能数据。等效性能计算方法有多种，本文将具有工程应用价值的两种等效性能计算方法(上文的三明治夹芯板模型等效性能计算方法和三明治夹芯板实体模型等效性能计算方法)集成到大型商业有限元前后处理软件MSC.Patran界面，如图3所示，实现输入基础数据后等效弹性性能自动加载到有限元软件，方便工程应用。

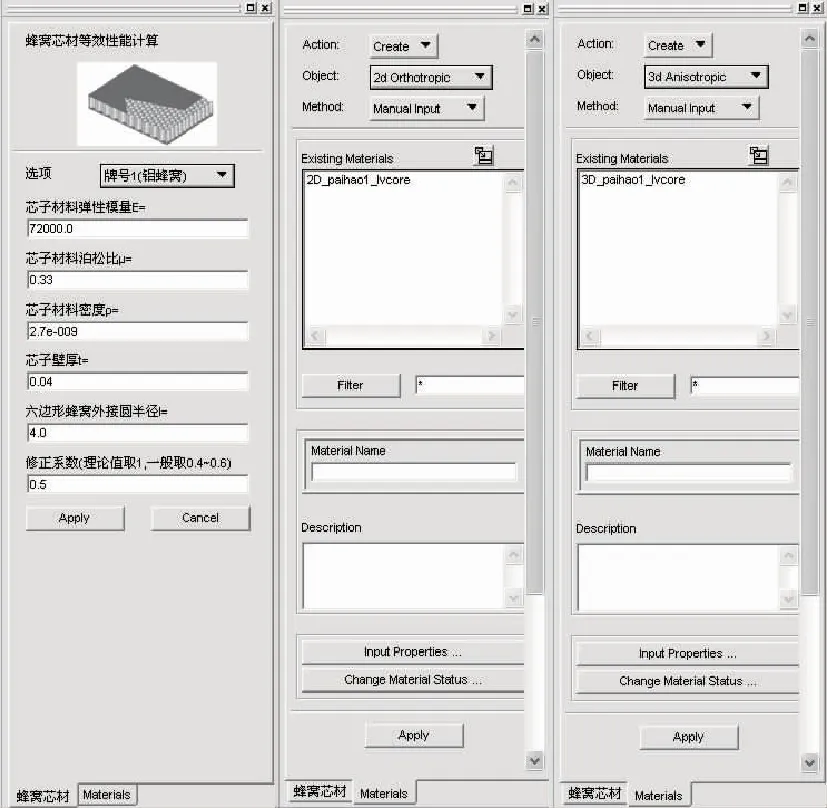
图3 芯子材料等效性能计算界面Fig.3 The new developed interface of equivalent characteristic calculation for cores

5 结论

本文通过对不同蜂窝夹层板校核模型得到的计算结果进行对比分析，得到如下研究结论，以便应用于相关飞行器结构设计。

1)3种模型在各阶频率下的振型相同，各阶频率分析结果均小于基准值，位移分析结果均大于基准值，说明3种等效模型下层合板的刚度偏弱。同时，3种模型X向应力计算结果高于基准，由于3种模型在主要承载方向X向刚度偏弱。可以得到结论：这3种理论模型是偏于保守的计算模型。

2)Hoff等效板模型规模小，适用于计算机技术不成熟的20世纪早期，同时该方法不能直接得到面板的应力，且应力误差较大。

3)三明治夹芯板模型与三明治夹芯板实体模型计算精度相当，刚度和强度计算结果误差相对Hoff等效板模型小，并且由于建模相对便捷，因此这两种模型成为工程应用首选。同时，本文基于这两种模型等效方法建立了芯子等效性能计算交互界面，使其工程应用更便捷。