基于稳健回归-去趋势波动分析法的山前平原地下水转换关系研究
2019-10-10刘晓芮陈植华
刘晓芮,王 清,陈植华,胡 成
(1.中国地质大学(武汉)环境学院,湖北 武汉 430074;2.中国地质调查局武汉地质调查中心,湖北 武汉 430205)
山前平原是山区向平原的过渡地段,既包括基岩山区,也包括平原河谷阶地。大别山-云应盆地山前平原过渡区内,东北部地势最高处为中元古界青白口系变质岩,向西南地势降低,为新生界古近系砂岩与变质岩不整合接触,伏于第四系松散堆积物之下,是研究区主要开采含水层。由于区域内第四系上更新统上部沉积物为相对隔水的亚黏土,其孔隙含水层与砂岩含水层相对封闭,主要开采层的地下水补给来源不明确,各类型含水层中地下水的转换关系缺乏较深入的研究。因此,查明区域内含水层中地下水之间的相互转换关系对地下水资源的合理开发和保护具有重要意义。
地下水动态变化特征的研究是目前地下水资源研究中具有挑战性的领域和热点之一[1-3]。地下水动态既反映出地区地下水资源的相关信息,也可对地下水之间的相互转换关系进行指示。地下水在补径排过程中,水位发生波动,水位过程线产生分形,由于地表、土壤、含水层等的阻滞作用,使各含水层中地下水水位时间序列的标度指数发生变化[4],因此可通过对不同类型含水层中地下水的分形标度进行量化,来分析探讨不同类型含水层中地下水之间的转换关系。
对于时间序列的分形标度行为的分析方法众多,去趋势波动分析(Detrended Fluctuation Analysis,DFA)方法能够有效检测嵌入非平稳时间序列中的长程相关性,避免由外部影响产生的虚假效果,被认为是一种可靠的非平稳信号的分析方法[5-7],在降雨、河流等水文时间序列分形方面的应用较为广泛,但在地下水时间序列分形方面的应用较少。Tu等[8]运用DFA法对承压含水层中地下水水位的单分形进行了量化,结果表明地下水水位时间序列存在分形,得到的地下水水位标度指数与时间序列的长度和时间间隔相关;Li等[4]运用DFA法对降雨-径流-地下水-基流的标度指数进行分析,认为地下水水位波动为分形布朗运动,由于土壤及含水层的抑制作用,降雨-地下水-基流的标度指数逐渐增大;Yu等[9]运用DFA法对波多黎不同类型含水层中地下水分形尺度进行了研究,结果表明冲积河谷含水层中地下水单分形指数高于岩溶含水层中地下水单分形指数。运用DFA法对单分形信号进行分析时,由于交叉点的确定是主观的,故会影响单分形量化的可靠性。为了克服此缺点并使量化过程自动化,Habib等[10]提出了稳健回归-去趋势波动分析(r-DFA)方法,并运用该方法对英国瓦林福德地区地下水及河流水位、地下水及河流水温、降雨和气温的分形尺度进行了量化,客观地确定交叉点,使其具有统计学意义,并在时间域和分形域对该地区降雨、空气、地下水、河流之间的相互联系进行分析。

1 研究方法
稳健回归-去趋势波动(robust Detrended Fluctuation Analysis,r-DFA)方法是包括DFA和统计模型的过程,能够对信号进行单分形量化,并自动确定交叉点位置。本文使用r-DFA方法的代码由Habib于2016年在Mathworks网站上提供(文件ID为60026)。
1.1 去趋势波动分析(DFA)过程
DFA法最早由Peng等[11]分析DNA相关性时提出,其计算步骤如下:

(1)
(2) 将Y(ti)分成m个时间长短为L的非重叠段,使m=int(N/L),每一段累积离差都标注为Yj,k,其中j表示分段长度,j= 1,2,…,L;k表示分段个数,k=1,2,…,m。

(2)
(4) 计算长度L中所有段的均方根F(L):
(3)
(5) 对不同的L值重复步骤(1)至(4),然后在对数轴上绘制F(L)与L的关系图,以确定标度指数α,即最佳拟合直线的斜率:
F(L)≈Lα
(4)
采用稳健回归(bisquare估计)线性拟合得到的α为r-DFA的全局标度指数,是忽略标度指数的任何局部变化而确定的直线斜率,可以确保其基于预定义范围内的残差。当α=0.5时,时间序列为白噪声,无长程相关性;α=1.5时,时间序列为分形布朗运动;当1.5<α<2时,一个时间序列是持续性的;当α<1.5时,时间序列是非持续性的。持续性表明,如果时间序列在一段时间内持续增加(或减少),则在类似的一段时间内,时间序列将继续增加(或减少);反之,非持续性则表明时间序列在类似时间内,时间序列与原趋势相反。
1.2 确定交叉点
全局标度指数α的变化指示出时间序列出现单分形行为,其表现为F(L)与L双对数关系图的斜率发生变化,发生变化的时间(L)为交叉点[4]。
在通过稳健回归拟合确定α后,还需要进行分段回归,通过最小化数据与拟合直线之间的最小二乘误差来优化交叉点位置;然后通过对DFA结果进行协方差分析(ANCOVA)和多重比较,确定拟合数据交叉点的数量,保证在95%显著性水平的基础上能产生显著差异的斜率的最大交叉点;将交叉点的数量逐渐增加,直到该方法不能产生任何进一步的显著标度指数。
1.3 去趋势波动分析(DFA)修正

(5)

2 研究区概况与数据来源
2.1 研究区水文地质概况
研究区位于云应盆地北部澴河河谷阶地,属于大别山山前平原区,气候为亚热带大陆性气候,雨热同期,地势北高南低,澴河从北向南纵穿,沿河两侧发育河漫滩与多级阶地,见图1。

受地形地貌及含水层结构特征的影响,研究区地下水接受大气降水补给后,总体上由北往南、由东西两侧往中部澴水方向径流及排泄(见图1)。
2.2 数据来源


图1 研究区水文地质平面简图及地下水水位长期观测孔分布

图2 澴河东侧水文地质剖面示意图
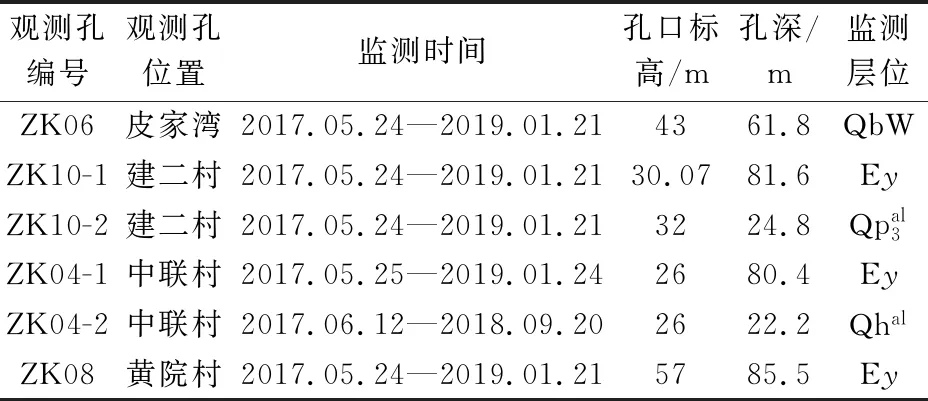
表1 研究区地下水水位长期观测孔基本信息统计表
地下水水位动态监测数据全部采用Levelogger solinst自动水位计进行采集,采集频率为1次/4 h;同时,收集了国家气象站孝感站2017年5月—2019年2月的4小时降雨量数据。
2.3 地下水水位动态数据的变化特征
研究区2017年5月—2019年2月降雨量和各类型含水层中地下水水位的动态监测数据,见图3。

图3 研究区2017年5月—2019年2月降雨量和各类型含水层中地下水水位的动态监测数据
由图3可以看出:
(1) 每次降雨前后,研究区西北部Ey砂岩孔隙-裂隙水含水层中地下水水位上升约0.05~0.1 m,波动微小;丰水期,Ey砂岩含水层中地下水水位于降雨增加约30 d后呈上升趋势,地下水水位上升幅度约0.5 m,持续上升约一个月后缓慢下降,地下水水位下降约0.7 m[见图3(c)]。结果表明:在降雨后研究区北部地区地下水得到补给,并向南部Ey砂岩含水层径流;枯水期北部补给区地下水接受降雨补给减少,Ey砂岩含水层中地下水水位开始缓慢下降。
(2) QbW变质岩类风化裂隙水含水层的富水性弱,对降雨的响应快,每次降雨后1 d内QbW变质岩含水层中地下水水位上升约0.3~0.5 m;2018年7—10月受到人为开采的影响,QbW变质岩含水层中地下水水位持续下降约2 m[见图3(b)];在丰水期,QbW变质岩含水层受到降雨持续补给,含水层中地下水水位上升约0.5 m,从峰值变化滞后降雨约30 d;在枯水期,地下水水位下降约为1 m。总体上看,青白口系变质岩含水层对降雨较为敏感,雨水转化为QbW变质岩类风化裂隙水。


在对昌马灌区近十年地下水水位年内变化分析时,分别以8眼监测井地下水水位2002—2010年期间逐月平均值(见图2)和2002年与 2010年年内地下水水位埋深作为指标进行分析,如图5所示。从图5中可以看出,以8眼监测井地下水水位年平均埋深作为指标来看,在研究时段内,Ⅰ-1、Ⅰ-2和Ⅰ-3监测井的水位年内随季节变化幅度较大,而其余监测井地下水水位年内随季节变化幅度不显著。同时,可以看出,以2002年和2010年为典型年的年内变化研究中可以看出,除Ⅰ-1、Ⅱ-1和Ⅱ-2监测井外,在两个典型年内,其余监测井地下水水位埋深的年内变化基本相同,且与多年年内地下水水位变化趋势基本一致。
3 结果与分析
3.1 不同阶数r-DFA结果比较
本文先对降雨量和6个地下水水位观测点的地下水水位动态数据进行DFA计算,再利用公式(5)来解决分形行为中的偏差,打乱顺序重新配置的次数选择为100,得到r-DFA1~r-DFA6,并采用稳健回归来确定所有阶的DFA的全局标度指数α;然后使用分段线性回归确定交叉点,并使用ANCOVA分析结果,再通过多重比较程序评估,最终得到研究区降雨r-DFA1~r-DFA6的F(n)(L)与L双对数关系图,见图4。
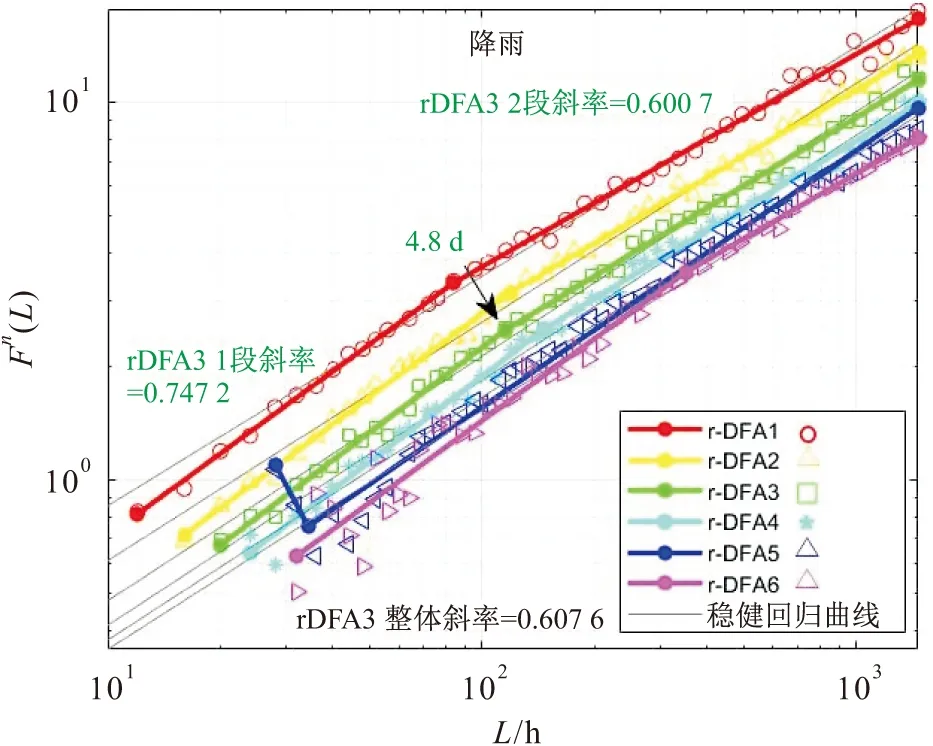
图4 研究区降雨r-DFA1~r-DFA6的F(n)(L)与L双对数关系图
由图4可见,经过修正后的高阶r-DFA拟合直线偏离共线趋势较小,与低阶r-DFA1、r-DFA2拟合结果相近;在高阶r-DFA拟合结果中,r-DFA4和r-DFA6原始数据与拟合直线在小时间尺度上拟合较差,r-DFA5拟合直线与其他阶拟合直线存在偏差,出现负斜率线段,而r-DFA3滤去了r-DFA1的线性趋势和r-DFA2的二阶趋势,与直线拟合最为接近,具有典型性和代表性,因此本文选择r-DFA3的拟合结果对斜率α值和各分段点斜率及交叉点横坐标进行分析。
3.2 降雨和地下水水位r-DFA3标度指数结果
研究区降雨r-DFA3的F(L)与L双对数关系图,见图5。

图5 研究区降雨r-DFA3的F(L)与L双对数关系图
由图5可见,研究区降雨的全局标度指数α值为0.607 6,类似于α=0.5的白噪声;研究区降雨序列在4.8 d左右发生交叉,当时间从小尺度上升到中等尺度时,降雨的α值从0.747 2下降到0.600 7。
研究区不同类型含水层中地下水水位r-DFA3的F(L)与L双对数关系图,见图6。
由图6可以看出:
(2) ZK06观测孔的QbW变质岩风化裂隙水含水层中地下水水位的α值为1.614 7,在19.5 d发生交叉[见图6(b)];在小时间尺度上,QbW变质岩含水层中地下水水位波动趋势是持续性的(α=1.641 3),在中等时间尺度上,其波动趋势是非持续性的(α=1.461 8)。
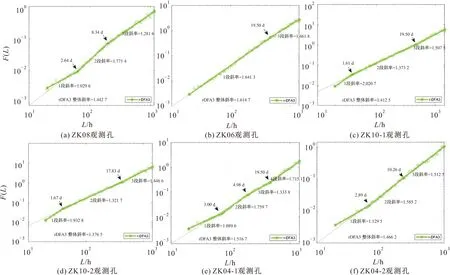
图6 研究区各观测孔地下水水位r-DFA3的F(L)与L双对数关系图

3.3 结果分析
研究区降雨和不同类型含水层中地下水水位r-DFA3的计算结果汇总于表2。
研究区降雨的全局标度指数α值为0.607 6,与Li等[4]和Matsoukas等[7]的研究结果一致。Matsoukas等研究了美国9个地区的降雨序列,在5~10 d左右均出现交叉,推测交叉点的出现与气象和气候系统的分离有关。

表2 研究区降雨和不同类型含水层中地下水水位的r-DFA3计算结果汇总
研究区不同类型含水层中地下水水位的全局标度指数α值表明,地下水水位波动更倾向于分形布朗运动(α=1.5),与前人的研究结果相同[4,8-9]。Li等[4]报道了美国爱荷华州地下水水位分别在6~30 d和50~365 d之间存在交叉点,其6~30 d的交叉结果与本文在较小时间尺度(4~10 d)的交叉结果相似,表明本研究区地下水分形特征与前人的研究结果一致,具有较高的可信度。
在所有的水文信号中,降雨的波动最大,在降雨入渗的过程中,由于地面、包气带和含水层的阻滞作用,将时间序列中较为复杂的波动滤掉,留下较为稳定的连续波动,其标度指数增大,通过比较标度指数,可体现含水层性质以及各类型含水层中地下水之间的转换关系。
研究区Ey砂岩含水层中观测孔ZK08与ZK04-1在第一交叉点前地下水水位波动趋势为非持续性,点后为持续性,第二交叉点后地下水水位波动趋势为非持续性,但两交叉点横坐标不同,且ZK08观测孔无第三交叉点,表明地下水分形具有场地特异性。
研究区QbW变质岩含水层的渗透系数在0.016~0.14 m/d之间,渗透性差且受到人为活动干扰最小,其地下水水位标度指数最大。


4 结 论
本文结合研究区降雨量和地下水水位数据的动态特征及r-DFA分析结果,得到如下结论:
(1) 研究区降雨波动类似于白噪声,地下水水位波动更倾向于分形布朗运动,且地下水分形存在场地特异性。

(3) r-DFA法通过对地下水水位的分形研究,得到其全局标度指数α,可定量地研究不同类型含水层中地下水之间的相互转换关系,本文的研究结果与定性分析结果一致,表明r-DFA法在分析各类型含水层中地下水之间的转换关系具有可行性和广阔的应用前景。
