激光扫描在工件表面检测中的应用方法

龚海强，单 奇，吴鹏飞，罗新河

(西南交通大学 机械工程学院，四川 成都 610031)

引言

磨削工件的表面质量是生产加工的重要指标之一[1-2]。同时，工件表面质量的好坏也直接关系到产品品质[3-4]。因此，如何确定磨削工件表面特征信息是表面检测领域中的重要研究对象[5-6]。曾碧[7]等人提出一种基于机器视觉的工件长时间跟踪算法，提高工件表面检测的准确性。董明明[8]等人提出一种基于颜色分离与特征统计分析的工件表面异物检测算法，提高工件表面异物检测准确性。然而，磨削工件表面检测还存在着许多实际问题。随着激光发展，激光测量技术被广泛应用于测量、尺寸检测等领域[9-10]，用激光测量技术取代传统的检测方法是提高效率、保证精度的有效途径[11-12]。Zhang Y C[13]等人将激光应用在尺寸测量上，实现了大型锻件热态尺寸测量。王仲等人[14]将激光传感器固定在机床主轴上，实现了大型工件轴孔心定位。但激光扫描测量在工件表面检测方面的应用研究较少。

本文针对工件表面特征检测领域，利用机械臂带动激光传感器扫描激光测量平面中的工件，通过工件边界点定位以及边界线拟合方法得出附着在工件上的坐标系相对于激光测量坐标系的偏移量以及旋转角度，通过两个坐标系之间的位姿信息进行坐标转换得出工件精确的三维坐标信息。该方法检测精度高且无需复杂的工件定位操作，为磨削工件表面检测提供了理论依据。

1 测量系统的构成

1.1 激光扫描系统的工作原理

如图1所示，激光源发出的激光采样线(下面简称采样线)经过被测物反射后在CCD上成像被测物上的点和在CCD上成像点的位置是一一对应关系。采样线上各个点到传感器的距离可以通过在CCD上面成像直线上各个图像点M1的具体位置求出来。

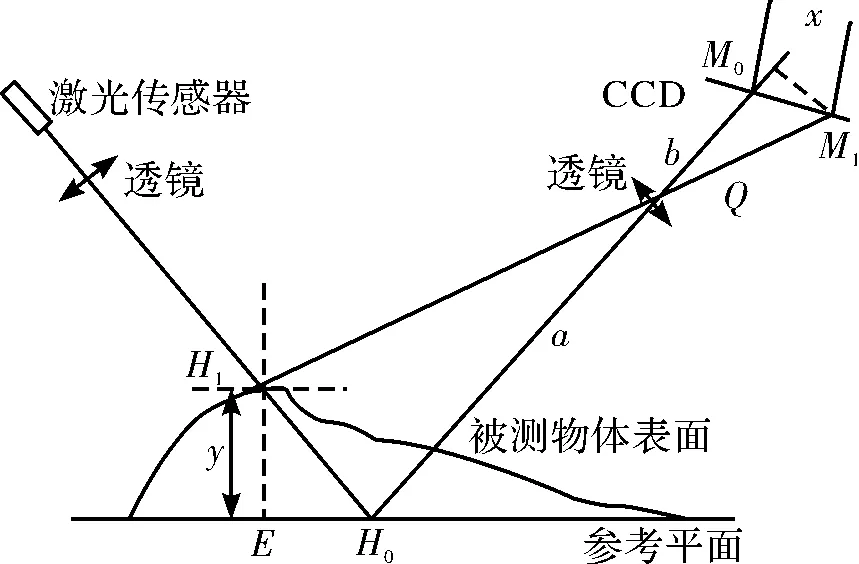
图1 激光扫描原理

1.2 激光测量平面

如图2所示，以采样线的起始位置为激光测量平面的左边界线，以采样线的结束位置为右边界线，机械臂带动激光传感器沿水平方向移动构成一个平面，将该平面定义为激光测量平面(下面简称测量平面)并以机械臂水平移动方向为激光测量坐标系的y轴，激光光束平行方向为激光测量坐标系的x轴。

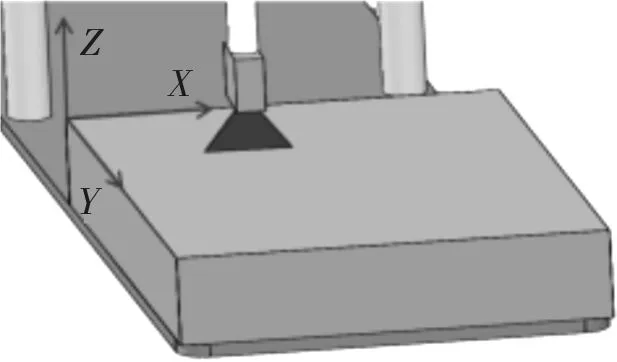
图2 激光测量平面

1.3 边界点识别与定位

如图3所示，对放置在测量平面中的工件扫描。扫描完成后即可采集工件边界点信息。

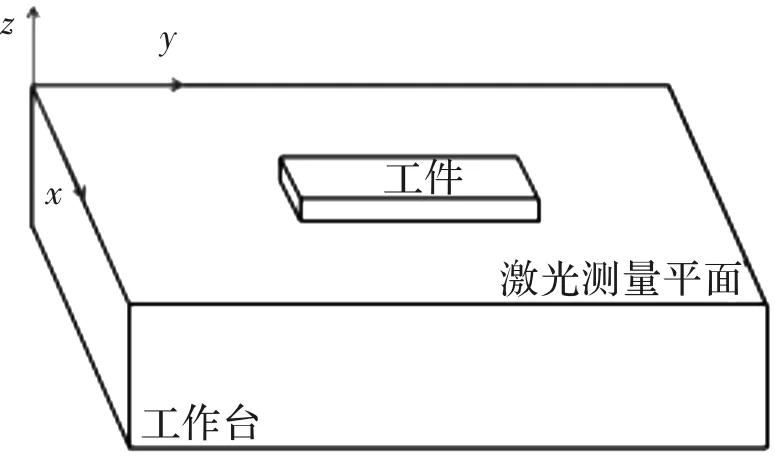
图3 边界点的识别与定位

本方法采用相邻2个采样点之间的高度变化来确定工件边界点[15]。即查找同一条采样线上所有相邻的采样点，查找公式表示为

Δz=(xi+1,yi+1,zi+1)-(xi,yi,zi)

(1)

式中：(xi,yi,zi)是采样线上第i个采样点，(xi+1,yi+1,zi+1)是同一采样线上第i+1个采样点。

根据公式(1)计算出相邻2个采样点之间的高度变化Δz，若|Δz|大于工件表面或测量平面表面粗糙度阈值，则可判断(xi,yi,zi)为边界点。将求出的所有工件边界点保存在边界点集合G=(xi,yi,zi)(i=0,1,…,j)中，其中(xi,yi,zi)为边界点。

1.4 工件表面点识别

图4为扫描过程中第i条采样线上工件截面图。如图4所示，工件边界点是工件表面和测量平面之间的过渡点。因此，利用工件边界点x轴坐标值的大小关系即可确定工件表面点。

图4 工件截面图

找出同一条采样线上x轴坐标值最大和最小的边界点，该采样线上介于这2个点之间(包括这2个点)的采样点即为工件表面点，将其保存在表面点集合W=(xi,yi,zi)(i=0,1,…,j)中，其中(xi,yi,zi)为工件表面点。

2 工件表面特征检测

2.1 旋转角度的判断

在本方案中利用最小二乘法对工件边界进行拟合，求出其边界在激光测量坐标系中的表达式，并根据表达式的斜率来确定旋转角度。

如图5和图6所示，工件相对于激光测量坐标系的旋转角度有θ≠0和θ=0两种情况。

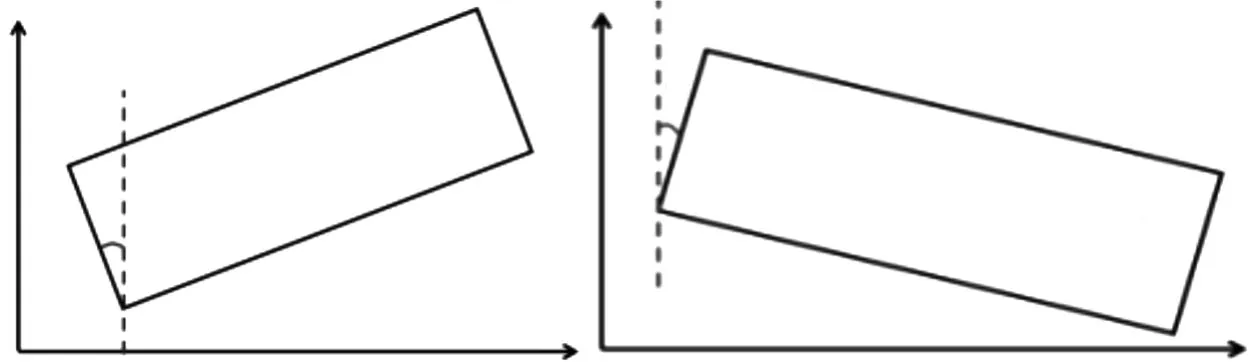
图5 旋转角度θ≠0

图6 旋转角度θ≠0

由上图可知，首先确定旋转角度θ是否等于0。系统遍历工件边界点集合G，找出其中x轴坐标的极值点，记为Xmax和Xmin，y轴坐标值的极值点，记为Ymax和Ymin，构造判别表达式：

|Ymax-Ymin|=Δi

(2)

|Xmax-Xmin|=Δz

(3)

Δ1-l=ε1

(4)

Δ2-h=ε2

(5)

式中：Ymax和Ymin是集合G中y轴坐标值最大和最小的点，Xmax和Xmin是x轴坐标值最大和最小的点，l是工件长度，h是工件宽度。

通过公式(4)和公式(5)判断|ε1|、|ε2|的值。若|ε1|≈0且|ε2|≈0，则可判断旋转角度θ=0，反之则判断旋转角度θ≠0。若旋转角度θ≠0，则进入下一步判别条件，判断旋转角度。工件坐标系旋转角度θ是否为0的确定算法如下所示：

1) 找出Ymax，Ymin，Ymax，Xmin。

2) 根据公式(2)和公式(4)求出|ε1|，根据公式(3)和公式(5)求出|ε2|，判断|ε1|≈0且|ε2|≈0是否成立。

3) 如果步骤2中条件成立则证明旋转角度θ=0，反之则跳转到步骤4。

4) 跳转到工件边界定位模型中利用Ymax、Ymin、Xmax、Xmin的坐标关系以及最小二乘法求出旋转角度。

2.2 工件定位边界模型

当旋转角度θ≠0时，旋转角度θ求解的先决条件是确定一条可以用最小二乘法拟合的边界线上点的坐标集合。下面首先介绍进行边界线拟合点的集合坐标确定。

由上小节的分析可知，在得出Ymax、Ymin、Xmax、Xmin这4个点之后，找出这4个点中y轴坐标最小的2个点，在边界点集合G中所有介于这两点间的边界点即为所需要进行曲线拟合的点，记为集合K。拟合的步骤为：

利用最小二乘法对集合K内的边界点构造一条边界线方程：

yj=a+bx

(6)

根据最小二乘法的原理，根据公式(6)，构造函数：

f(a,b)=∑(yi-yj)2=∑(yi-a-bxi)2

(7)

根据公式(7)，对f(a,b)函数生成极值函数：

(8)

由公式(8)即可求得a、b，从而求出拟合边界线的表达式。

2.3 旋转角度求解

在拟合出边界线的方程后，根据公式(9)可以求得旋转角度θ。

k=tanθ

(9)

式中：k是边界线斜率；θ是旋转角度。

1) 当工件处于图5(a)位置时，θ=arctank+90°；

2) 当工件处于图5(b)位置时，θ=arctank-90°。

2.4 位姿变换

为了描述工件在激光测量坐标系{A}中的位姿信息，在工件上附着一个参考坐标系{B}(如图6所示)。下面详细介绍姿态变换的旋转矩阵和位置变换的位置矢量的确定方法。

构造一个旋转矩阵用来确定工件在激光测量坐标系中的姿态信息，如公式(10)所示：

(10)

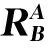
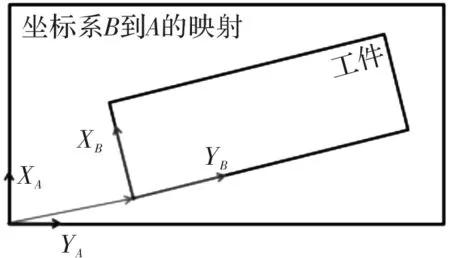
图7 坐标系映射

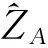
(11)

(12)

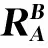
(13)

位置矢量用来确定坐标系{B}的原点在激光测量坐标系{A}中的位置，此处用符号APB来表示。位置矢量的描述如公式(12)所示：

(14)

式中：px、py、pz是坐标系{B}原点在激光测量坐标系{A}的x、y、z主轴上的投影。同理，由于是二维的位姿变换，故而pz=0。

对于旋转角度θ≠0和θ=0两种情况。

1) 当θ=0时，坐标系{B}的位置分量px、py用Xmin的x轴和y轴的坐标值来描述。

2) 当θ≠0时，斜率k存在2种情况：当k>0时，坐标系{B}的位置分量px、py用Ymin的x轴和y轴的坐标值来描述；当k<0时，坐标系{B}的位置分量px、py用Xmin的x轴和y轴的坐标值来描述；

根据上面的分析可以求得位置矢量的分量px、py。由于只存在x、y平面的姿态描述，所以位置矢量的分量pz=0。

将上述求得位置矢量的分量px、py、pz代入公式(12)中，即可得本方法中位置矢量APB。

根据坐标系变换的物理属性可知：

BPA=-APB=[-px-py-pz]T

(15)

2.5 坐标系间的映射

由于用激光传感器扫描出来的工件表面点位是在坐标系{A}中进行描述的，在求出坐标系之间的位置和姿态的相对变换后，可以根据公式(16)来求出坐标系{A}中点位的矢量在坐标系{B}中的描述。

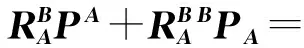
(16)

式中：PA=[XAYAZA]T表示的是坐标系{A}中描述的点的位置矢量。

将上述求解得到的旋转角度θ与位移量px、py带入公式(13)可得

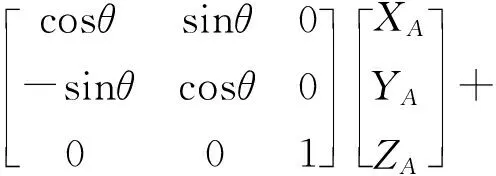
3 实验及分析

3.1 试验平台

如图8所示，工件表面检测系统由机械臂、激光传感器、上位机、激光测量平面及扫描工件组成。其中，上位机用于对激光传感器采集到的数据进行分析处理，从而得出工件表面特征信息。

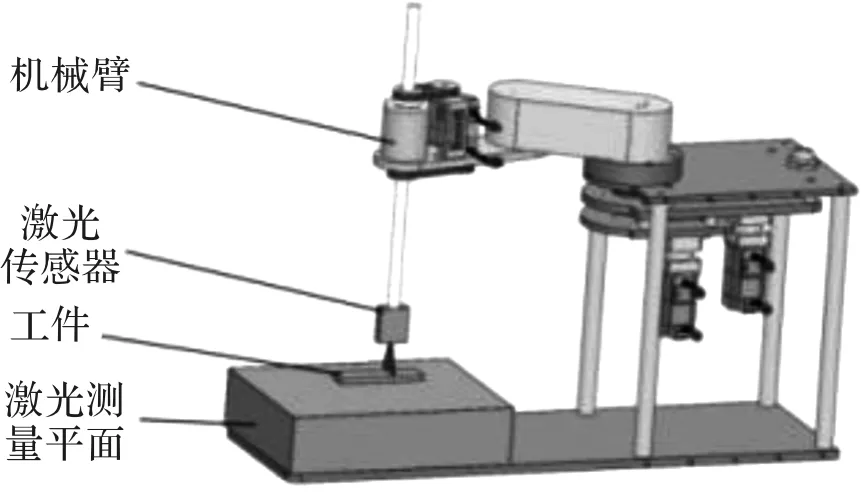
图8 实验装置

3.2 试验测试

在对工件边界线进行拟合之前，首先对工件边界极值点定位的准确性进行测试。测试结果如图9所示。

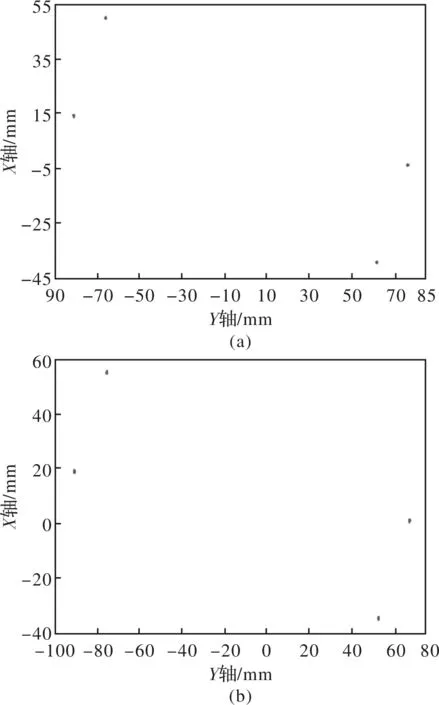
图9 边界极值点定位

为了验证工件边界线拟合是否符合预期要求，对该拟合方法进行测试。实验中对两种不同位姿的工件边界线进行拟合，拟合结果如图10所示。

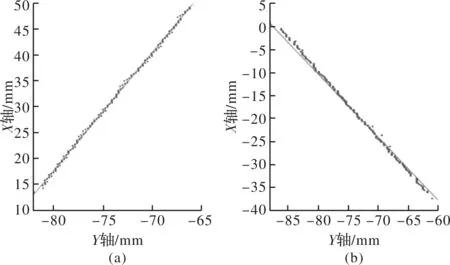
图10 工件边界线拟合

为了验证表面检测是否符合预期要求，对该方法进行测试。检测结果如图11所示。

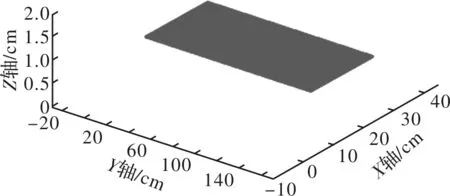
图11 工件表面检测

3.3 误差分析

在测量过程中，误差不可避免。本方案对系统测量过程中误差产生的原因进行分析，主要有以下几个部分：

1) 机械臂误差：主要由于机械臂的制造精度产生的误差，其中包括加工、装配以及机械臂之间的传动等引起的误差。机械臂水平方向引起的测量误差δ1=100 μm；机械臂垂直方向引起的测量误差δ2=100 μm。

2) 激光传感器误差：主要包括激光传感器制造精度造成的加工误差和激光传感器安装在机械臂上造成的安装误差。激光传感器沿x轴方向测量误差δ3=4 μm；沿z轴方向的测量误差δ4=10 μm；激光光束横截面的宽度为200 μm，因此，由激光传感器造成的沿y轴方向上的最大测量误差为δ5=200 μm。

3) 环境误差和工件材料：主要包括测量过程中的温度、湿度、光照及工件表面反射率引起的误差。由于测量装置被放置在室内，故环境误差对实验影响较小。

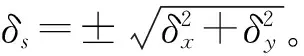
3.4 工件表面检测误差

在测量过程中，机械臂带动激光传感器进行工件扫描时，工件表面检测误差主要由机械臂垂直方向引起的测量误差δ2和激光传感器沿z轴方向误差δ4确定的，故工件表面检测误差δ=δ2+δ4=110 μm。

4 结论

本文采用激光传感器实现非接触测量，保证了工件表面检测精度，并利用机械臂带动激光传感器扫描工件实现了工件表面特征检测并生成工件表面精确的三维坐标信息。实验结果表明，该方法检测时间短且识别精度高，为工件表面特征检测提供了新的思路，具有良好的参考价值。