无透镜显微成像的重构算法研究
2019-10-10王丹萍谢梦圆李志斌朱文国余健辉
王丹萍,谢梦圆,李志斌,朱文国,余健辉,陈 哲,张 军
(暨南大学 理工学院 广州市可见光通信重点实验室,广东 广州 510632)
引言
无透镜显微成像系统是一种不需要使用任何透镜聚光、直接使用成像传感器对物体进行成像的系统。传统显微镜成像分辨率较高(200 nm),但是视场较小(最大约为5 mm2)[1-3],与之相比,无透镜显微成像的优点在于结构简单,同时具有大视场。因此,现今许多研究都致力于利用无透镜显微成像系统进行细胞计数和疾病诊断[4-12],并将之直接集成为一个医疗器件[9,11,13]。但是无透镜显微成像系统存在分辨率低的问题,一般只有几十微米。现有的研究主要通过两种方式提高无透镜显微成像系统的分辨率:改进实验装置[14-16]和改善图像重构算法[16-19]。在改进实验装置方面,Mudanyali等人在待检测样品前插入1.1 μm起偏器,实现1.5 μm的成像分辨率[1];在改善图像重构算法方面,主要是将多幅图像进行叠层处理,从而提高分辨率。如Antonio等人[2]拍摄不同角度的样品图片,再使用快速鲁棒算法(SURF)和蚁群算法进行图像的叠层处理,获得了1.55 μm的图像分辨率,突破了实验所用complementary metal oxide semiconductor(CMOS)的分辨率极限(1.56 μm)。使用多幅无透镜叠层算法进行图像重构时,虽然能够达到甚至突破CMOS本身的分辨率极限,但与单幅的无透镜图像重构相比,增加了图像处理过程的复杂度,降低了成像速度。而国内对于单幅无透镜成像算法方面的研究也较多[20-26],但是单幅图像的分辨率都较低,如重庆大学张德燕等人[20]制作的集成型无透镜显微成像系统的分辨率为40 μm;陈云鹏等人[25]也搭建了无透镜显微成像系统,利用angle spectrum method(ASM)算法得到的分辨率为6.96 μm。虽然单幅无透镜显微成像系统的装置结构简单,但是分辨率仍需进一步提高。
由于文献[27]中,无透镜非相干成像使用了Lucy-Richardson(简称L-R)算法进行图像重构,因此,本文将对L-R算法做部分修改,将其作为无透镜相干成像重构算法的一种,并与ASM重构结果进行对比,从而确定最佳的单幅无透镜显微成像重构算法。结果表明,在本无透镜显微成像系统中,ASM重构图像的分辨率最高(即3.10 μm),运行时间最短(即0.9 s)。同时,本文进一步利用小鼠胚胎成纤维细胞(简称3T3细胞)对系统进行了验证。结果表明,所获得的图像分辨率介于5×与10×显微镜之间,且无透镜显微成像系统的视场比10×蔡司显微镜大16倍,比5×蔡司显微镜大4.4倍。因此无透镜显微成像系统在细胞观察/计数方面其统计学优势明显高于传统显微镜,在生物医学领域具有广阔的应用前景。
1 实验装置及算法原理
1.1 实验装置
本文的无透镜显微成像系统装置如图1所示,由成像传感器CMOS、样品和光源组成。所用CMOS的型号为TP605100A,视场为24.4 mm2,空间分辨率为2 592×1 944像素,像素点大小为2.2 μm,帧速最快为60 fps,光源是中心波长为450 nm的蓝光LED。将实验中需要使用的样品置于光源与CMOS之间,光源距离CMOS 320 mm,样品与CMOS之间的距离约为1 mm。在进行图像拍摄实验时,将USAF分辨率板或包含细胞的计数板作为样品,当光源发出的光透过样品后,在CMOS表面发生衍射,由CMOS记录图像,获取无透镜拍摄的原图。
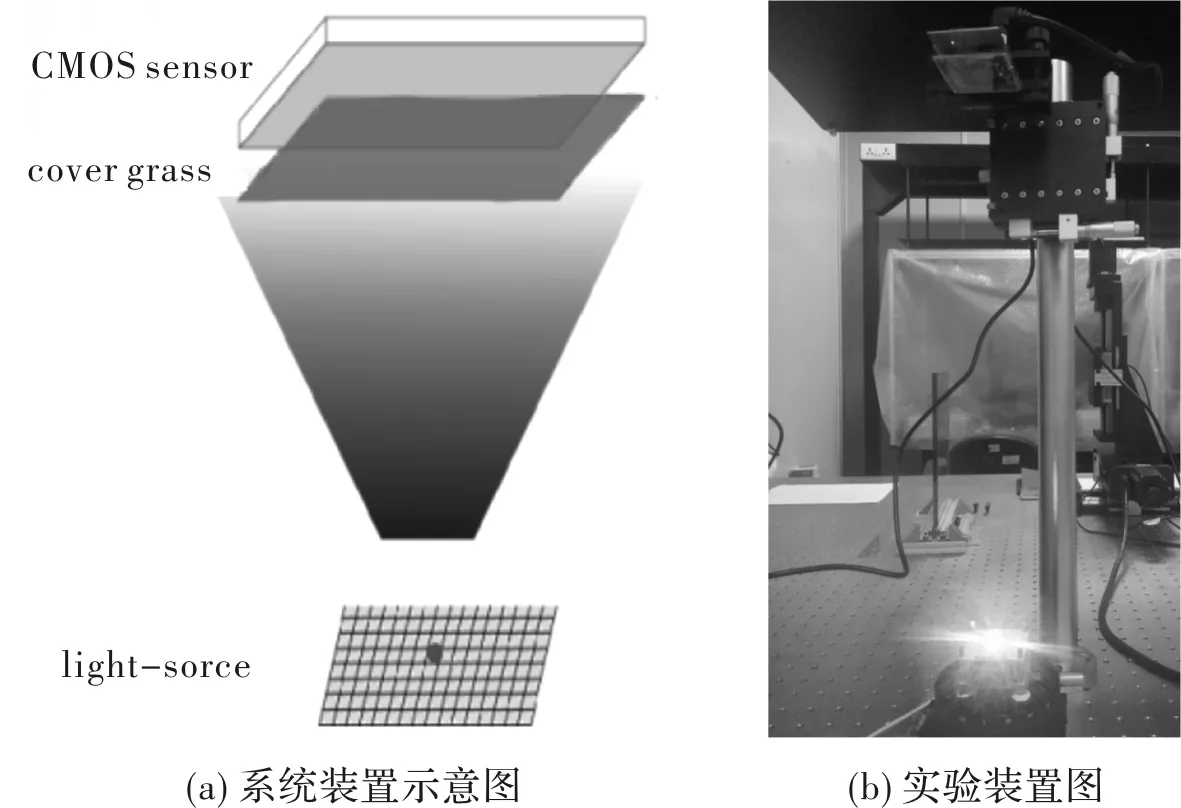
图1 无透镜显微成像系统的装置图
1.2 算法原理
L-R算法进行解卷积的原理如下:
1) 设物函数为object,物函数的振幅为objectAmp,⊗表示卷积,则
object=objectAmp·eiφ
(1)
(1)式表示一个物体是由振幅objectAmp以及相位φ组成。
2) 经过空间中的传输,获取的图像Im(x,y)设定为物函数object(x,y)与点扩散函数PSF(x,y)的卷积,即:
Im(x,y)=object(x,y)⊗PSF(x,y)
(2)
其中点扩散函数PSF为

(jλ·(x2+y2+z2))
(3)
式中:波数k=2π/λ;x,y为每个像素点对应的空间坐标;z为物和像之间的传输距离;λ为入射光波长。
3) 取迭代次数为i,i≥2,将获取的图像Im(x,y)赋值给obji(x,y),并将图像回传到物面,反推物函数,反推迭代公式如下:
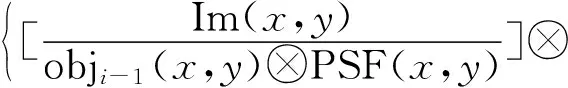
PSF(x,y)}·obji-1(x,y)
(4)
4) 迭代结果输出还原的物函数的强度图abs(obji(x,y))和相位图ang(obji(x,y))。
由于L-R算法在迭代的过程中有滤波模糊的作用,因此迭代次数不宜过多,否则图像丢失的信息增多导致图像模糊不清,因此本文只使用2次迭代。
ASM重构的原理如图2所示,x0、y0所构成的平面为物平面,x1、y1所构成的平面为记录平面,物平面上存在某点P(x,y,0),经过光照射后,P点在记录平面上的投影为P′(x,y,z)。设P点的振幅为U(x,y,0),P′点的振幅为U′(x,y,z),P的空间频谱为A(fx,fy,0),P′的空间频谱为A′(fx,fy,z)。fx是对应像素点的频谱横坐标,fy是对应像素点的频谱纵坐标。具体计算过程如下:
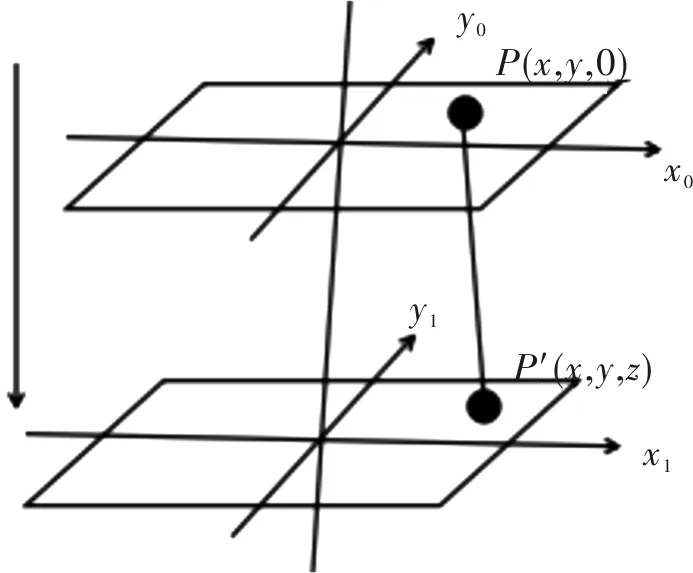
图2 ASM重构的原理图
1)P′的振幅U′(x,y,z)可表示为

fyy)]dfxdfy
(5)
由标量衍射理论在平面波传播中的推导可得[28]:
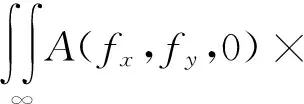
(6)
2) 对比(5)式和(6)式可得,P′的空间频谱A′(fx,fy,z)可表示为

(7)
3) 通过(7)式可得波传播的传递函数H可表示为
(8)
4) 在离散条件下,再现物P点的空间振幅u(x,y,0)可以表示为
u(x,y,0)=IFT(FT(u(x,y,z))×
H(fx,fy))
(9)
同理,再现物P点对应的空间振幅u可输出物点的强度图abs(u(x,y,0))和相位图ang(a(x,y,0))。
2 实验结果
2.1 分辨率分析
图3为无透镜显微成像系统拍摄的分辨率板原图及L-R算法重构后的结果。

图3 无透镜显微成像系统拍摄的分辨率板原图及L-R算法重构后的结果
由图3(a)可得,无透镜拍摄原图的分辨率为12.40 μm(组5元素3),原图中组5 元素4及后面的元素由于振铃效应,图中出现4条纹及或2条纹,因此需要使用重构算法来消除和减弱振铃效应,提高图像的分辨率。图3(b)和图3(c)是图3(a)经过L-R算法重构后得到的振幅图和相位图。由图3(b)可知, L-R算法重构所得振幅图分辨率为11.05 μm(组5 元素4);由图3(c)可得, L-R算法重构的相位图分辨率为6.96 μm(组6元素2)。由此可知,L-R算法重构时,在一定程度上减弱了振铃效应,提高了分辨率。
图4为无透镜显微成像系统拍摄的原图及ASM重构的结果,其中图4(a)是无透镜显微成像系统拍摄的原始图像,图4(b)和图4(c)分别为经过ASM重构所得的振幅图和相位图。由图4(c)可知,相位图中的振铃效应没有任何改善,分辨率仍为12.40 μm(组5元素3);图4(b)的振幅图在很大程度上减弱了振铃效应,使图像得到复原,但是具体分辨率仍需进一步分析。

图4 无透镜显微成像系统拍摄的原图及ASM重构的结果
为了对图4(b)的分辨率做出科学的判断,本文将瑞利判据作为极限分辨率的判断依据。由于图4(b)中组6元素及组7元素1已清晰可辨,本节将针对图4(b)的组7 元素2(竖向元素)、组7元素3(包括竖向元素和横向元素)和组7元素4(横向元素),取1行/列像素点(针对竖/横向元素),图5(a)中分别用粗实线、粗虚线、细实线和细虚线4条画线表示。4条画线对应的像素点与灰度值的关系曲线分别如图5(b)、(c)、(d)、(e)所示。对比图5(b)~(e),根据瑞利判据,两个波峰相交的波谷对应的值所占波峰值的73.7%以下属于可分辨。由此可得:组7元素2和组7元素3(横向元素)可以分辨;组7元素 3(竖向元素)和组7元素4不可分辨。因此无透镜显微成像系统结合ASM的方法,可以获得水平方向为3.48 μm(组7元素2)和垂直方向为3.10 μm(组7元素3)的分辨率。因此,ASM算法获得的振幅图分辨率为3.10 μm,即在本无透镜显微成像系统装置中,单幅图像的极限分辨率为3.10 μm。
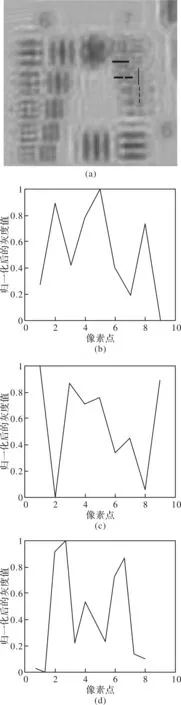
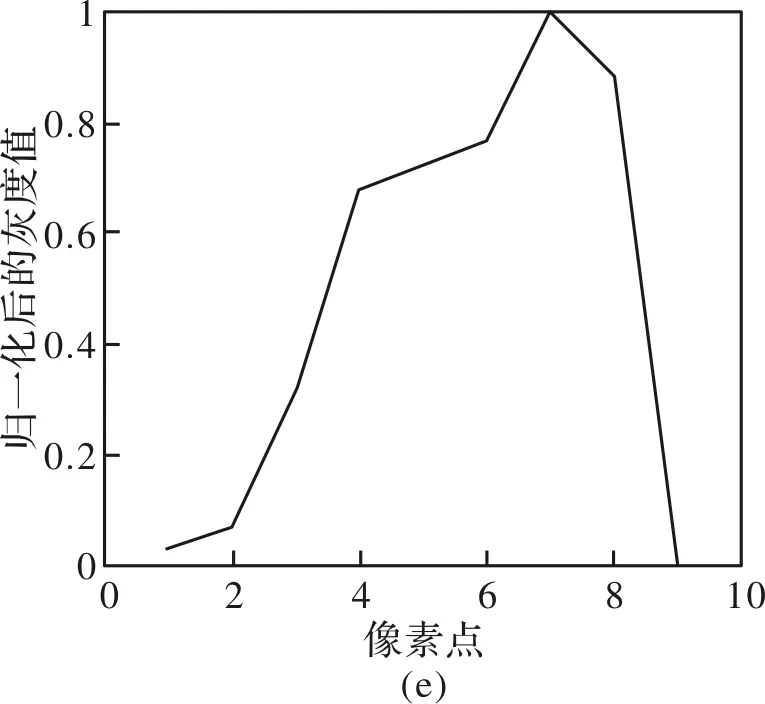
图5 (a)为对应图4(b)中第6级和第7级元素的放大;(b)、(c)、(d)、(e)分别为(a)中粗实线、粗虚线、细实线、细虚线上的像素点与灰度值的关系曲线
综上所述,当使用L-R算法进行图像重构时,振幅图的分辨率为11.05 μm,相位图的分辨率为6.96 μm;ASM进行图像重构后,振幅图的分辨率为3.10 μm,相位图的分辨率12.40 μm。由此可得,ASM重构图像分辨率最高,为3.10 μm。同时,L-R算法的运行时间为3 h,ASM算法仅为0.9 s。因此,无论是在分辨率还是在计算用时方面,ASM都优于L-R算法,为最佳的单幅无透镜图像重构算法。由于一般细胞大小约为十几个微米,而本无透镜显微成像系统的极限分辨率为3.10 μm,因此可将无透镜显微成像系统替代传统显微镜进行细胞成像,实现细胞实时观察。
2.2 细胞观察
本节利用无透镜显微成像系统对小鼠胚胎成纤维细胞(3T3细胞)进行观察。图6是无透镜显微成像系统拍摄的包含3T3细胞的细胞计数板图像及使用ASM重构后的结果。由于无透镜成像系统的视场大小取决于CMOS的成像面积,所以该系统的视场与COMS的视场大小一致,为24.4 mm2。使用10×蔡司显微镜(AxioCam MRc 5)的视场大小约为1.5 mm2,5×蔡司显微镜的视场大小约为5.6 mm2;使用分辨率板标定的10×蔡司显微镜的分辨率约为2.19 μm,5×蔡司显微镜的分辨率为3.91 μm。由此可得,无透镜显微成像系统结合ASM算法进行图像重构时,所得图像的分辨率介于5×与10×显微镜之间,且无透镜显微成像系统的视场尺寸比10×蔡司显微镜大16倍,比5×蔡司显微镜大4.4倍。在细胞计数方面,显微观察时视场越大,计数会更加准确(更具有统计学意义),因此在使用传统显微镜进行细胞计数时,一般选用低倍显微镜以获得大视场。本无透镜显微成像系统结合ASM所获取图像的分辨率比5×显微镜高,同时视场是5×显微镜的4.4倍,因此无透镜显微成像系统在细胞观察/计数方面其统计学优势高于传统显微镜。除此之外,该无透镜显微成像系统结构简单,经过光学设计后,其高度可减小为十几个厘米,更有利于将其放入CO2细胞培养箱中,对细胞的生长进行实时观察,并集成为便携式医疗器械。

图6 无透镜拍摄的细胞经过ASM解卷积的结果
3 结论
本文介绍了一种无透镜显微成像系统,并针对单幅无透镜显微图像的重构算法进行研究,分别使用了L-R和ASM两种算法进行图像重构。其中L-R算法重构所得的振幅图分辨率为11.05 μm,相位图分辨率为6.96 μm,运行时间3.0 h;ASM算法获得的振幅图分辨率为3.10 μm,相位图分辨率12.40 μm,运行时间0.9 s。因此,无论是在分辨率还是在计算用时方面,ASM均为最佳的单幅无透镜显微重构算法,单幅图像的极限分辨率为3.10 μm。同时利用无透镜显微成像系统结合ASM重构的方法,对小含有鼠3T3细胞的细胞计数板进行显微成像。所获得的无透镜图像分辨率介于5×与10×显微镜之间,同时视场是5×显微镜的4.4倍。因此无透镜显微成像系统在细胞观察/计数方面优于传统显微镜,统计学优势明显。本文无透镜显微成像系统结合ASM算法进行图像重构的方法,不仅能够实现更高的分辨率,还具有更大的视场,在生物医学领域具有广阔的应用前景。
