单目移动机器人相对位姿估计方法

王 君，徐晓凤，董明利，孙 鹏，陈 敏

(1.北京信息科技大学 仪器科学与光电工程学院，北京100192；2.长春理工大学 光电工程学院，吉林 长春 130022；3.北京信息科技大学 机电系统测控北京市重点实验室，北京100192)

引言

同步定位与地图构建SLAM[1-2](simultaneous localization and mapping)使得移动机器人能在没有先验知识的未知环境中或自身位置不确定的条件下，借助传感器增量式构建或更新环境地图，同时利用地图进行自主定位、导航、避障和规划路径等。

SLAM系统主要依赖视觉传感器与激光雷达两种传感器对周围环境进行感知[3-4]。相比激光雷达，视觉传感器以其价格便宜、体积小并且能够获取更加丰富的信息等特点，展现出了在小型机器人上的强大优势[5-6]。因此，基于视觉的SLAM系统构建成为了机器人自主定位和导航的重要方法。对于单目移动机器人，通过相邻两幅或多幅关键帧图像恢复相机相对位姿成为视觉SLAM系统中建立视觉里程计的核心问题。

传统的位姿估计方法通常是通过五点法、八点法等算法获得本质矩阵[7-8]，然后分解本质矩阵得到相机相对位姿参数。机器人在运动过程中需以较快的速度采集图像信息，以满足实时更新地图与定位的需求。因此，相邻关键帧图像之间基线一般较短，常规方法求解本质矩阵存在困难[9]。

本文结合单目机器人定位需求，提出一种利用特定参照物或运动信息获取本质矩阵并进一步分解相对位姿的估算方法，解决传统方法中由于基线过小无法恢复相机相对位姿的问题。该方法首先利用已知特定参照信息，初始化本质矩阵的估计值；然后，通过相邻关键帧间匹配的特征点组和本质矩阵估计值迭代优化本质矩阵；最后通过本质矩阵的约束关系求得平移向量估计值，并建立目标函数，利用基于李群的姿态表示得到旋转矩阵估计值，优化出唯一解。

1 本质矩阵估计

1.1 本质矩阵

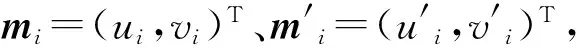
(1)

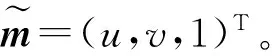
(2)

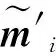
(3)

而本质矩阵E由旋转平移矩阵R、t得:

E=t×R=[t]×R

(4)

所以，得到本质矩阵的重要约束条件:

(5)

1.2 单幅图像位参估计

对于已知的特定参照物，利用其空间坐标以及在单幅图像中的像面坐标进行空间后方交会，获取外参数旋转角度(φ、ω、κ)和平移量(Xs、Ys、Zs)。

共线条件方程[11]有:

(6)

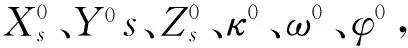
[ΔXsΔYsΔZsΔκΔωΔφ]T+

(7)

其中x0、y0是将外参数近似值带入共线方程得到的x、y。

由共线方程的线性形式可列出误差方程：

[ΔXsΔYsΔZsΔκΔωΔφ]T-

(8)

式中：x、y为特征点的像面坐标；vx、vy为像面坐标的改正数；ΔXs、ΔYs、ΔZs、Δκ、Δω，Δφ为外参数修正值。(7)～(8)式两组方程为一个控制点列出，如果有n个控制点，则可以列出2n个方程，故n≥3且不共线时即可求出外参数。

利用所得外参数计算出单幅图像位姿参数Rφωκ和Tφωκ：

(9)

Tφωκ=[XsYsZs]T

(10)

式中用sκ、cκ等表示对应旋转角度的正弦和余弦。

1.3 本质矩阵估计

得到单幅图像的位姿参数后，可利用两幅图像的旋转平移关系计算出相对位移，即：

(11)

由(11)式得

(12)

(13)

(14)

2 相机相对位姿解算

由于最终的本质矩阵需由特征点组参与迭代优化，所以对特征点组的匹配精确度有较高要求。为了得到有效的匹配特征点组，首先利用SURF (speed up robust features)算法[12]进行特征点的提取和相邻关键帧之间的匹配，获得初始特征点组；然后，通过RANSAC(random sample consensus)算法[13]去除特征点组中的误匹配；最后，利用(5)式的约束条件对特征点组做进一步筛取，获得精确匹配的特征点组。

2.1 本质矩阵优化

任何本质矩阵均有奇异值分解[14]：

(15)

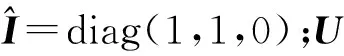
(16)

其中：Rx、Ry、Rz分别为3个轴方向的位移向量；Rκ、Rω和Rφ分别为绕x、y、z轴旋转得到的旋转矩阵，有：

式中：sκ、cκ是对应旋转角度的正弦和余弦；Rx和Ry的形式与Rκ和Rω相同；θ=(θκ,θω,θφ,θx,θy)中5个旋转参数均为构成本质矩阵E的基本参数。本文将利用这些本质矩阵的局部参数对其进行迭代优化。

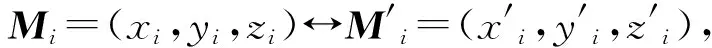
(17)

当θ=0时，对参数向量θ=(θκ,θω,θφ,θx,θy)进行求导，可得：

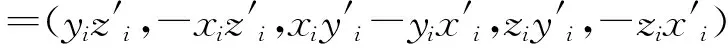
(18)

矩阵J是通过对应Ji|0的每i行进行叠加所得。

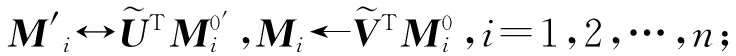
3) 计算向量误差ε；

(19)

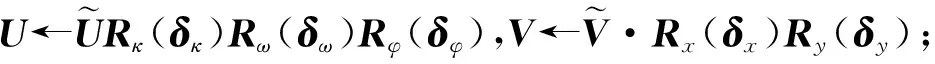
6) 重复2～5步，直到收敛。

2.2 相对位姿计算

利用ETT=0估计出平移向量T的两个解：

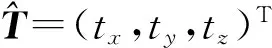
(20)

矩阵E和矩阵[T]×R满足关系式E-[T]×R=03×3。建立目标函数，对目标函数寻优来确定旋转矩阵：

R=arg minR‖E-[T]×R‖2

(21)

对R有，R=R0R(ξ)，其中：R0为初值；姿态角度假设为0；R为单位阵。R(ξ)利用李群方法可表示为

(22)

式中ξ=(ξ1,ξ2,ξ3)为运动增量，对应于相机图像间角速度。基矩阵Gj如下所示：

对d(ξ)=E-[T]×R0R(ξ)进行线性处理：

d(ξ)≈d(0)+d·ξ

(23)

令雅可比矩阵J=d，则

(24)

令Q1=[T]×R0G1，Q2=[T]×R0G2，Q3=[T]×R0G3，则J可以表示为

得：

(25)

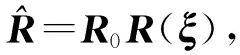
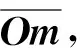
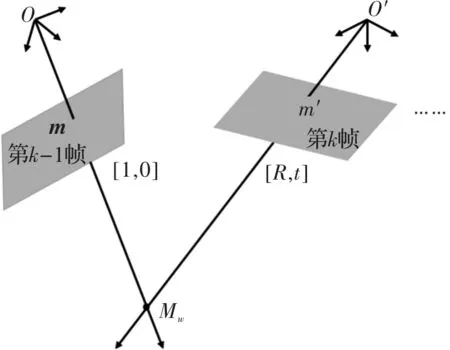
图1 匹配点的几何关系

同一世界坐标系中，m与m′对应的相机坐标分别为

(26)

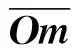
(27)

3 实验结果

布置已知三维关系的特定点群(图2)(3 m×3 m)作为特定参照物用来检验位姿，只要机器人视野范围内识别到其中5个点即可得到相机相对位姿，从而减小了设置特定点群带来的局限性。

图2 特定点群

为了检验实验结果的可靠性和有效性，将本文算法得到的结果与V-Stars静态摄影测量系统处理的结果进行比较。V-Stars系统是美国GSI公司研制的工业数字近景摄影测量系统[15]，可快速、高精度(相对精度可达1/200 000)地计算出相邻关键帧之间的相对位姿转换参数。

机器人采用USB接口的GY200工业相机作为视觉传感器，其有效像素为44万。机器人在地面移动轨迹约3.12 m，对实验现场(图3)采集图像，并选取16幅关键帧。机器人在移动过程中进行同步定位与地图构建，相对位移误差是影响定位与地图构建精度的主要因素。因此，实验主要通过机器人相机相对位移误差评价位姿估计结果。

图3 实验现场

3.1 特征点提取与匹配

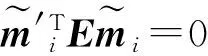
图4 匹配结果

3.2 相机相对位移精度评估

将V-Stars系统处理得到的相机相对位姿作为真实值，控制匹配点数，统计不同匹配点数下传统五点法与本文算法获得相机相对位移的估计精度，结果如图5所示。

实验结果表明，随着特征点对数量的增加，相机相对位移估计的误差逐渐减小，并在特征点数大于200后误差变化逐渐趋于稳定。

将传统五点法与本文算法优化前、后估计得到的相机运动轨迹和相机运动的真实路径进行比较，从而进一步检验本文算法对相机位移估计的精度与鲁棒性。图6、7展示了移动机器人在地面上X方向和Y方向上的位移数据比较。

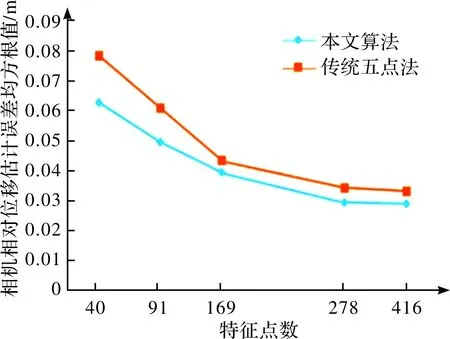
图5 特征点数与相机相对位移估计误差的关系

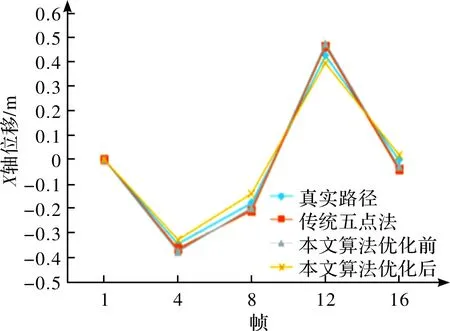
图6 X轴方向上的位移

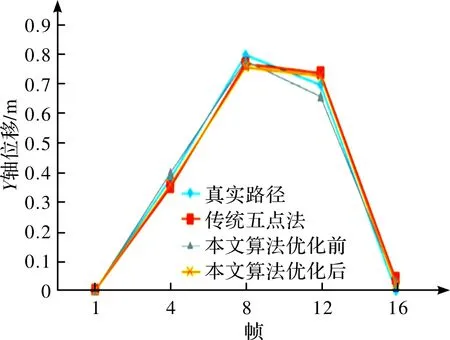
图7 Y轴方向上的位移

利用相机相对位移估计绝对误差的均方根值(RMSE)、中值(Median)和最大值(Max)3个指标进行比较评估，实验结果如表1和表2所示。

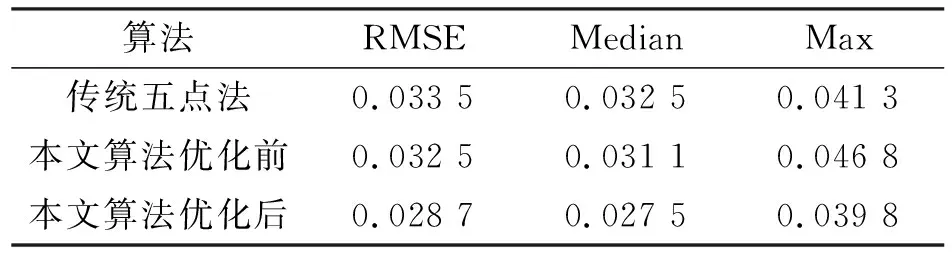
表1 X轴方向相机相对位移估计误差 m

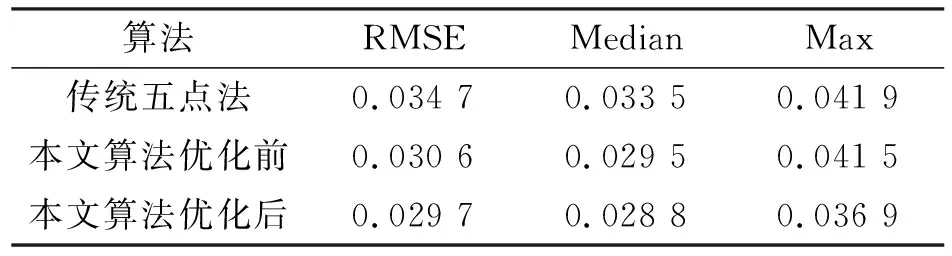
表2 Y轴方向相机相对位姿估计误差 m

实验结果表明，本文算法优化后的相机相对位移估计绝对误差RMSE、Median值均小于0.03 m，优于传统五点法。

3.3 算法可靠性分析

从算法本身来讲，具有较强适应性，不仅适用于非共面参照物，还适用于参照物特征共面的退化情况，仅对于参照物特征共线的退化情况不适用。而且，算法对于参照物的分布数量、密集程度没有特殊要求，理论上只需要匹配5个特征点就可以实现定向和位姿估计。

但是，通过大量实验发现，影响算法可靠性的关键并不在于本质矩阵优化本身，因为优化目标函数是单峰函数，局部最小值就是全局最小值，算法本身的优化结果是可靠的。影响最终结果的关键在于本质矩阵初值估计，而影响初值估计的主要问题在于特征识别和匹配，一旦存在误匹配，即使数量很少，也会对本质矩阵估计产生较大影响，造成后续优化失败。因此，如何确保用于初值估计的特征匹配结果准确率是算法可靠性的关键。

4 结论

本文提出了一种利用已知特定参照物迭代优化本质矩阵，快速分解机器人相对位移参数的方法，该方法不受限于机器人视觉关键帧图像之间基线过短等问题，大大提高了机器人单目SLAM系统在选取关键帧的灵活性，使其只需考虑图像重叠使用率。同时，该方法也保证了获取的相机相对位移参数具有较高的精度。而如何结合鲁棒性算法(M-估计法、最小中值法、最大后验概率法等)提高特征匹配的准确率，并提高算法可靠性等是进一步研究的方向。