高功率固体激光器增益非均匀分布引起的效能亏损效应研究

位永辉，王石语，过 振，蔡德芳，李兵斌，吴梦瑶

(西安电子科技大学 物理与光电工程学院，陕西 西安710071)

引言

激光设备在军事装备中的应用呈现迅猛发展的趋势，已经应用到的武器装备包括：激光测距仪、激光目标指示器、激光制导导弹、激光制导炸弹等。随着激光技术的发展，特别是在武器系统中，激光器向大能量方向的发展将会带来革命性的变化。但是，考虑军事应用的背景，在发展大功率或大能量激光器的同时，必须确保激光器具有高的能量转换效率和好的光束质量，这是发展高效能军用固体激光器的技术瓶颈。

为获得高功率激光输出，需要增加泵浦功率。但是，非均匀的泵浦在提供增益的同时，由于热损耗和模式畸变损耗，会引起激光效能亏损，这一效应在高功率泵浦固体激光器中尤为突出。本文建立理论模型，研究高功率的非均匀泵浦光作用下，由热效应和增益引起的模式的效能亏损，为高功率泵浦固体激光器的设计提供参考依据。

1 非均匀泵浦下热效应引起的效能亏损

1.1 计算模型的建立

激光二极管泵浦固体激光器中，激光晶体的热稳态泊松方程为

(1)

式中：T(x,y,z)为晶体内的温度；Q(x,y,z)为热源功率函数；k为激光晶体的热传导系数。泵浦光为四阶的归一化光强分布，即：

(2)

I(x,y,z)=I0exp(-2r4/ω4)exp(-αz)

(3)

式中α为晶体材料的吸收系数。晶体内的热源Q(x,y,z)由晶体对泵浦光吸收而产生，因此，可得到热源函数表达式：

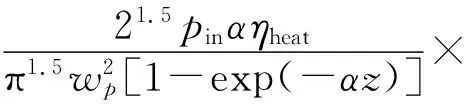
(4)

式中：η为热转换系数；pin为泵浦光功率；wp为泵浦光半径；I(x,y,z)为晶体内(x,y,z)点处的泵浦光强度。晶体内温度的不均匀分布引起晶体内折射率的改变，晶体内(x,y,z)点处的折射率为

(5)

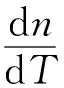
(6)

故光程差引起振荡光的相位差为

(7)

求得相位差之后可求出热效应的相位调制因子，由相位调制因子可进一步求解振荡光的热致损耗，即：

ψ(x,y)=exp(-iΔφ(x,y))

(8)

1.2 数值计算与分析

1.2.1 晶体内温度场分布

使用四阶平顶高斯光进行端面泵浦时，泵浦光的光场分布函数为

E(r)=E0exp(-r4/w4)

(9)

热源函数的表达式为

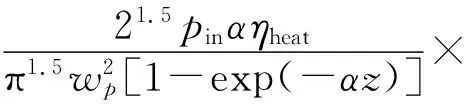
(10)

使用的激光晶体参数为直径3 mm，长10 mm的圆柱形Nd:YAG晶体，晶体的吸收系数为0.73 mm-1，掺杂浓度为1%。泵浦光功率为30 W，泵浦光半径为0.5 mm时晶体端面的温差分布如图1所示。

图1 晶体内温差分布

由图1可以看出，Nd:YAG晶体为各向同性的晶体介质，端面泵浦情况下，其截面处的温度分布为圆对称分布，具有高斯分布形式，从中心向边缘逐渐减小。晶体中心温度比边缘温度要高得多，并且沿径向迅速减小，即晶体内各个截面内存在很大的温度梯度。

晶体端面处的温度差的最大值高达66.1℃，而z=5 mm截面处温度差最大值仅为0.83℃。由此可见，激光晶体具有热吸收作用，随着泵浦光束沿z轴的传播，晶体内温度差随着晶体的吸收作用迅速减小，且沿z方向截面上的温度场分布越来越均匀。

泵浦光半径为0.5 mm时，不同泵浦光功率下晶体端面温差沿径向的分布曲线如图2所示。

图2 不同泵浦光功率下的温度差沿径向分布曲线

由图2可知，当泵浦光功率增加时，热效应会继续加强，晶体内的温度不断升高，泵浦功率为30 W时，晶体端面最高温度达到66.1℃；当泵浦光功率为70 W时，晶体端面最高温度达到154.2℃。若晶体不能及时冷却，很容易导致晶体形变损坏，并且影响激光器输出光束的质量。

不同泵浦光半径下晶体端面温差沿径向的分布曲线如图3所示。由图3可知，随着泵浦光半径的增大，晶体中心的温度降低，沿径向的温差分布趋势越来越平缓。

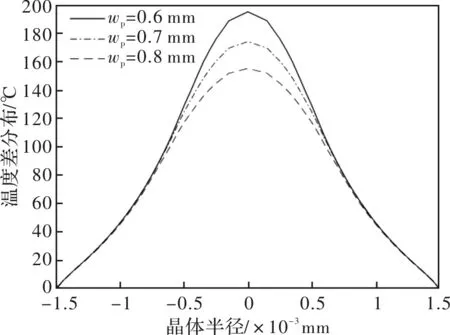
图3 不同泵浦光半径下温度差沿径向分布曲线

1.2.2 热效应引起的光程差与相位差的分布

热效应引起的的光程差分布与相位差分布规律同温度场分布基本相同，如图4和图5所示。从图5可以看出，高斯光在晶体中心处的相位差最大，附加相移随着径向坐标的增大而逐渐减小，越接近晶体边缘，附加相移慢慢趋近于零。

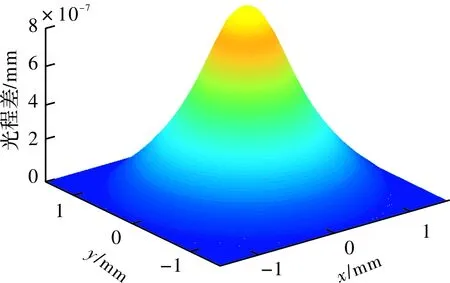
图4 总光程差分布图

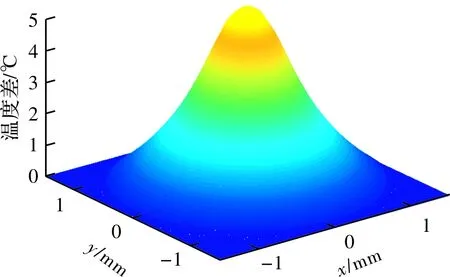
图5 相位差分布图

随着泵浦光功率和泵浦光半径的改变，相位差分布的变化趋势和温度场的变化趋势相同，如图6所示。从图6可以看出，随着泵浦光功率的增大，热效应引起的相位差迅速增大，相位差沿径向的分布曲线越来越陡；随着泵浦光半径的增大，相位差沿径向的分布曲线慢慢趋于平缓。因此，泵浦光功率和泵浦光半径严重地影响着晶体内相位差的分布。

图6 相位差沿径向分布曲线

1.3 热效应引起的激光模式损耗

由于热效应的影响，振荡光会受到相位差的调制，进而改变谐振腔内振荡模式的组分。通常，振荡光可以表示为谐振腔内几种基本模式的线性叠加，为简化计算，假设初始时谐振腔内只存在低阶模TEM00、TEM01和TEM02其中的一种模式，振荡光通过晶体后这3种低阶模光场视为有效输出，其余部分视为能量损耗。下面分别研究TEM00、TEM01和TEM02模转换到其他模的比例系数。这里假设振荡光为基模高斯光，建立热效应对激光模式转换的计算模型。

当端面未泵浦时，晶体内折射率分布均匀，基模高斯光在晶体内传输时，晶体的各个截面被认为是等相位面。初始光场分布函数为

φ00(x,y)=C00e-r2/w2

(11)

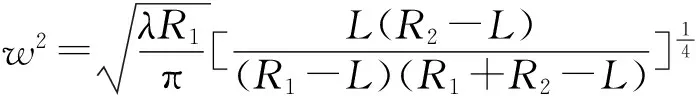
当理想高斯光泵浦晶体端面时，晶体对泵浦光的吸收作用导致晶体内温度分布不均匀，进而导致晶体内各个截面上的温度分布也不均匀，会对振荡光产生相位调制。对调制之后的光场分布函数进行归一化处理，得到光场分布函数为

(12)

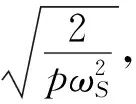
(13)

(14)

(15)

给定泵浦光功率为100 W，平凹腔的谐振腔腔长为0.1 m，输出镜曲率半径为0.8 m，泵浦光半径分别为0.6 mm，0.7 mm，0.8 mm时，计算热效应引起的3个模式的损耗分别如图7所示。

图7 不同泵浦光半径下各阶模损耗随泵浦光功率的变化曲线

由图7可以看出，当泵浦光半径保持不变时，3个模式的损耗随着泵浦光功率的增大而增大；当泵浦光功率不变时，3个模式的损耗随着泵浦光半径的增加而减小。当泵浦光功率和泵浦光半径相同时，TEM02模的损耗最大，其次是TEM01，TEM00最小。功率较小时，TEM02模的损耗增加的最快，其次是TEM01模，TEM00模的损耗增加的最慢。功率较大时，3个模式损耗增加的趋势渐渐趋于平缓。

2 激光增益引起的效能亏损

2.1 计算模型的建立

四能级系统的Nd:YAG激光器中，激光器的速率方程为

(16)

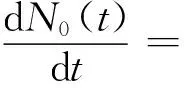
(17)

式中：n(x,y,z,t)为上能级粒子数密度；p(x,y,z)为泵浦速率密度；τf为上能级荧光寿命；c为真空光速；σ为受激辐射截面；S0(x,y,z,t)为震荡光子数密度；ng为增益介质的折射率；δ0为基膜腔内往返ELGD率；N0(t)为腔内振荡光子总数；l为谐振腔长度；积分区域为整个增益介质。

2.1.2 增益分布函数

文中泵浦光为四阶平顶高斯光，泵浦光入射到晶体内，激光晶体吸收泵浦光能量，从而引起晶体内上能级粒子数反转。由于晶体介质对泵浦光的吸收作用，泵浦光经过晶体介质时光强逐渐减弱，晶体内各个截面上的吸收光强各不相同，因此各个截面上的上能级粒子数分布不均匀。泵浦激光晶体端面上的归一化泵浦光光强分布为

(18)

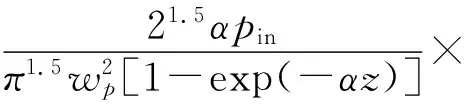
(19)

式中：pin为泵浦光功率；wp为泵浦光半径；α为晶体的吸收系数，ηheat为热转换系数；ηheat=1-λp/λs；λp为泵浦光波长，808 nm；λs为振荡光波长，1 064 nm。

转速下，涡轮盘盘心处温度为760 ℃，叶片温度为790 ℃～810 ℃。离心载荷以转速的形式施加到模型上，为100%设计点转速，约束中心端面的轴向位移和周向位移。

当泵浦晶体端面时，介质内的粒子吸收泵浦光能量后，从基态跃迁到激发态上，形成粒子数反转。随着泵浦的持续，上能级粒子数不断增多，但由于上能级粒子数有一定的寿命，超过寿命的粒子又会回到基态，最后上能级粒子数会达到最大值并且保持动态平衡。当泵浦时间足够长时,可得到晶体内部上能级粒子数密度为

(20)

式中τ为上能级粒子的荧光寿命。对于脉冲激光器，其上能级粒子数密度为

(21)

式中T为脉冲周期。设脉冲激光器的重复频率为10 000 HZ，T为1/10 000 HZ=100 μs。在受激辐射跃迁中，上能级粒子数的变化量会转化为光子数的增加量，用φ(x,y)表示(x,y)处的光子数面密度，则有：

dφ(x,y)=σφ(x,y)dN(x,y)

(22)

φ(x,y)=φ0(x,y)eσN(x,y)

(23)

增益系数的表达式为

(24)

由于晶体纵向长度上各个截面上晶体吸收的能量不同，上能级粒子数分布有所差异，因此，各个截面上的增益分布也各不相同。对n(x,y,z,t)在z方向上积分可以求得介质晶体内振荡光的总增益分布为

(25)

2.1.3 激光增益引起的效能亏损

泵浦光泵浦至晶体端面，晶体内上能级粒子数不断积累，最后到达最大值不变。腔内振荡光经过增益介质到达输出镜上，将此时的振荡光投影到输出镜上的3个正交归一化的TEM00、TEM01和TEM02模光场上，未投影到这3个光场的部分视为增益引起的效能亏损,简称ELGD(efficiency loss caused by gain distribution)。

假设谐振腔内只存在基模振荡光，归一化的基模振荡光光场分布为

(26)

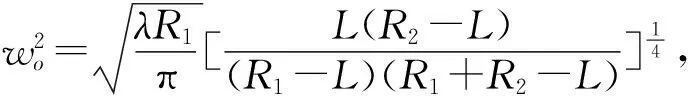
(27)

振荡光向腔镜面在3个正交模式TEM00、TEM01和TEM02上的投影系数分别为

(28)

(29)

(30)

故增益引起的效能亏损(以下简称ELGD)为

(31)

用同样的方法，可以求出TEM01、TEM02的ELGD。

2.2 数值计算与分析

2.2.1 晶体内上能级粒子数分布及增益分布

假设泵浦光为四阶平顶高斯光，输出镜曲率半径为0.5 m，腔长为0.05 m。给定泵浦光功率为50 W，泵浦光半径为0.5 mm时用MATLAB模拟得到晶体内上能级粒子数分布和增益分布如图9和图10所示。

由图9和图10可以看出，上能级粒子数分布与增益分布具有大致相同的分布规律，与平顶高斯光强的分布相同。上能级粒子数分布及增益分布与泵浦光的分布有十分密切的联系。晶体中心区域增益最大，越靠近边缘，上能级粒子数和增益分布越少。

泵浦光半径为0.5 mm时，泵浦光功率分别为60 W、80 W、100 W时增益分布沿径向分布曲线如图11所示。泵浦光功率为100 W，泵浦光半径分别为0.6 mm、0.7 mm、0.8 mm时增益分布沿径向的分布曲线如图12所示。

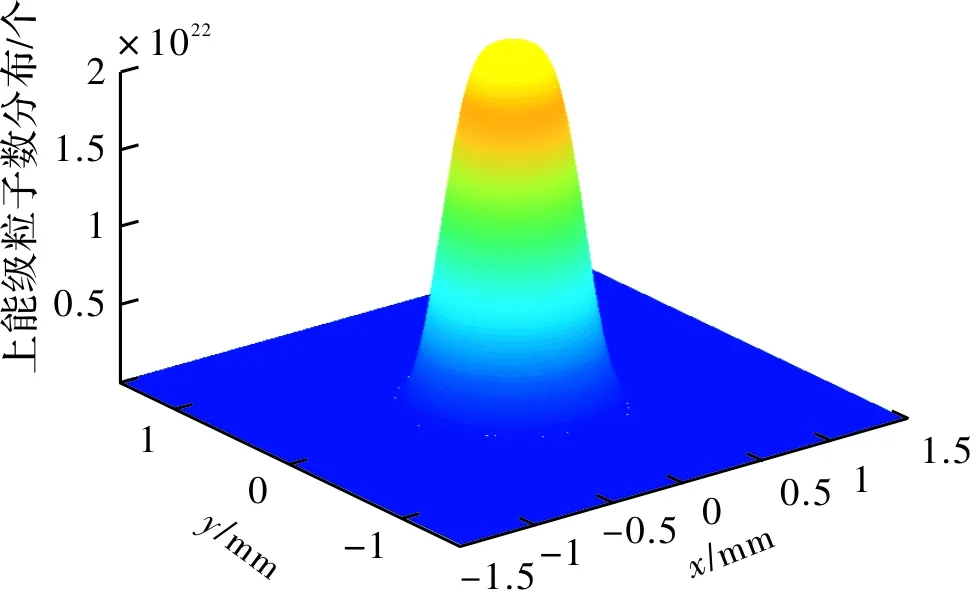
图9 上能级粒子数分布(P=50 W)

图10 增益分布(P=50 W)

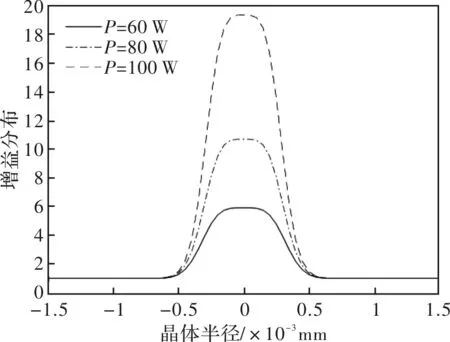
图11 不同泵浦光功率下增益沿晶体径向分布曲线(wp=0.5 mm)

图12 不同泵浦光半径下增益沿晶体径向分布曲线(P=100 W)

由图11可以看出，随着泵浦光功率的增加，增益沿径向的分布曲线越来越尖锐，介质晶体内的增益迅速增大。由图12可知，增益的分布随着泵浦光半径的增加而减小，曲线越来越平缓。

2.2.2 连续光泵浦晶体端面时各阶振荡光经过介质增益后ELGD的变化规律

前面研究了振荡光增益的分布特性，下面研究连续光经过增益后各阶振荡光在谐振腔内ELGD的变化与泵浦光功率和泵浦光半径的关系。

1) 泵浦光功率和泵浦光半径

给定谐振腔腔长为0.05 m，输出镜的曲率半径为1 m，泵浦光半径分别为0.6 mm，0.7 mm，0.8 mm时，TEM00、TEM01和TEM02模振荡光经过增益后的ELGD的变化如图13所示。

由图13可以看出，泵浦光功率和泵浦光半径相同时，TEM00模的ELGD远远小于TEM01、TEM02，TEM02的ELGD最大。当泵浦光半径不变时，TEM00、TEM01和TEM02的ELGD都随着泵浦光功率的增加而增加；当泵浦光功率不变时，3个模式的ELGD都随着泵浦光半径的增加而减小。当泵浦光半径不变，泵浦光功率较小时，TEM02的ELGD增加的速度最快；当泵浦光功率不变时，随着泵浦光半径的增加，TEM02的ELGD减小的速度最慢。

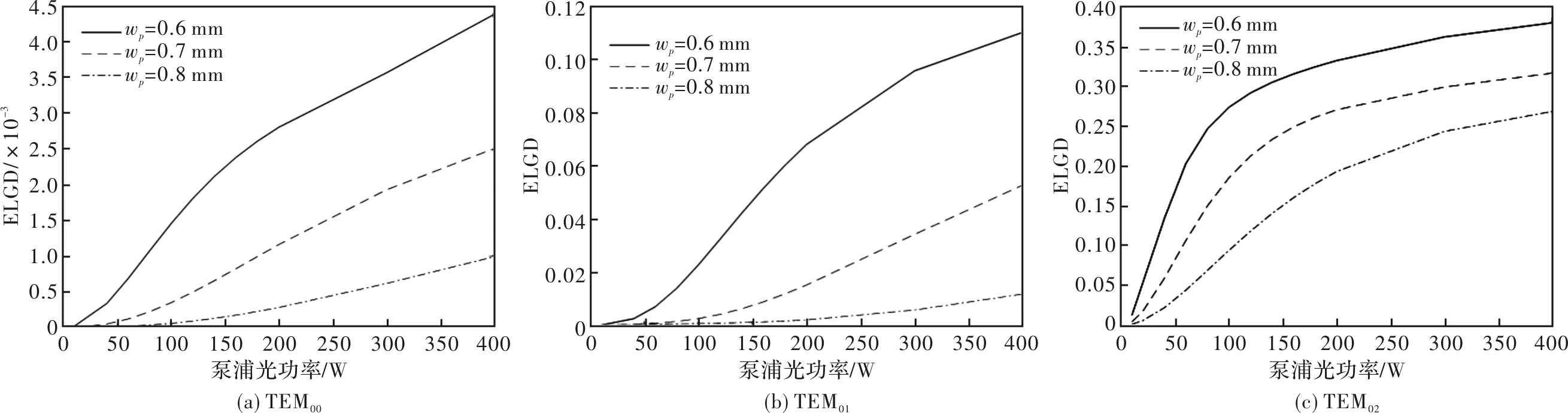
图13 不同泵浦光半径下,各阶模ELGD随泵浦光功率的变化曲线

2.2.3 脉冲光泵浦晶体端面时各阶振荡光经过介质增益后ELGD的变化规律

下面分析脉冲光经过介质增益后各阶振荡光在谐振腔内ELGD的变化与泵浦光功率和泵浦光半径的关系。

给定谐振腔腔长为0.05 m，输出镜的曲率半径为1 m，泵浦光半径分别为0.6 mm，0.7 mm，0.8 mm时，TEM00、TEM01和TEM02模振荡光经过增益后，由增益引起的效能亏损(ELGD)随腔长的变化如图14所示。

图14 不同泵浦光半径下各阶模ELGD随泵浦光功率的变化曲线

由图14可以看出，脉冲光泵浦晶体端面时，3个模式的ELGD随泵浦光功率和泵浦光半径的变化规律与连续光泵浦晶体端面时的规律基本相同。泵浦光功率和泵浦光半径相同的情况下，TEM00的ELGD远远小于TEM01和TEM02，TEM02的ELGD最大。泵浦光半径不变时，TEM00、TEM01和TEM023个模式的ELGD都随着泵浦光功率的增大而增大；泵浦光功率一定时，泵浦光半径越大，3个模式的ELGD越小。同时还可以看出，小功率泵浦时，TEM02的ELGD增加的速度最快，TEM00最慢，功率较大时，TEM02的ELGD增长的速度越来越趋于平缓。

对比连续光泵浦时ELGD与泵浦光功率和泵浦光半径的关系可以看出，相同条件下，脉冲光泵浦晶体端面时3个模式的ELGD比连续光泵浦时的ELGD要小得多。因此，使用脉冲激光器能够获得更好的输出光束质量。

4 结论

考虑在热透镜影响下，分析增益引起的激光模式的ELGD与泵浦光功率和泵浦光半径的关系，当泵浦光半径不变时，3个模式的ELGD随着泵浦光功率的增加而增大；当泵浦光功率不变时，3个模式的ELGD随着泵浦光半径的增加而减小。对比连续光泵浦和脉冲光泵浦的情况可以看出，脉冲光泵浦晶体端面时ELGD较小，可以获得较好的输出光束质量。