基于分级的福建将乐地区栲树树高曲线模型研究

李 杰

(中关村绿色碳汇研究院，北京100029)

树高曲线是指胸径与树高关系的曲线。在制定森林经营计划时，树高和胸径是两个经常用到的林分因子，也是常用来计算林分蓄积、立地指数及其他与森林生长、收获、演替、碳储量等相关指标的重要变量[1-3]。通过研究基于分级的将乐地区树高曲线模型，对于编制福建省将乐地区亚热带常绿阔叶林森林经营数表及指导当地森林经营具有重要意义。

多年来，研究者们建立了许多线性和非线性的树高曲线模型[4-7]，试图找出一个更符合生物学特性的方程式来诠释树高的生长规律，这些模型主要有Richard、Weibull、Logistic、Korf和Gompertz等模型。在这些模型中，解释变量通常是胸径，并将模型的参数解释为最大生长量、生长率及生长率的变化率等[8-12]。但很多研究表明，树高的生长还与立地条件、林分密度、森林类型、风速等环境因素有密切的关系[13-17]。

栲树(Castanopsisfargesii)是我国东南亚热带常绿阔叶林的重要树种，目前对于福建省将乐地区的栲树树高曲线尚未有系统深入的研究[18-21]。笔者以福建省将乐国有林场常绿阔叶林的主要树种栲树为研究对象，采用分级的思想构建栲树树高曲线离散模型，再将地形因子引入到离散模型中，建立地形等级与树高的关系用以估测研究区的树高，旨在为将乐地区栲树常绿阔叶林经营和其他主要树种的树高研究提供参考。

1 研究区概况

研究区位于福建省将乐国有林场，属武夷山支脉，为闽西北低山丘陵地带，地处金溪河畔，地理坐标为117°05′～117°40′E，26°26′～27°04′N。该区属于中亚热带沿海海洋性季风气候，具有海洋性和大陆性气候特点，年平均气温18.7 ℃，年平均降雨量1 669 mm，年平均蒸发量1 204 mm，气候温润。土壤质地为沙壤土或者轻壤土，土层深厚，土壤肥沃。

将乐林场总面积7 113.6 hm2，有林地6 568.9 hm2，森林覆盖率达到93.8%，其中常绿阔叶林占13.09%，主要树种有栲树(C.fargesii)、木荷(Schimasuperba)、拟赤杨(Alniphyllumfortunei)、甜槠(Castanopsiseyrei)、米槠(Castanopsiscarlesii)、青冈(Cyclobalanopsischungii)等[22-23]。

2 研究方法

2.1 数据来源

数据采集自福建省三明市将乐国有林场。综合考虑研究区内栲树的区域分布、立地条件、采伐及人为干扰等因素，选择并设置以栲树为主要组成树种的样地17个，样地规格为20 m×30 m。对样地内胸径大于5 cm的栲树进行每木检尺，共调查栲树427株。样地调查内容包含地理坐标、树高、胸径、海拔、坡度、坡向、坡位等因子，具体详见表1。

表1 福建将乐地区栲树样地和样本的基本信息

以427株栲树的相关数据作为样本拟合模型，设置拟合样本299个(占总样本的70%)，验证样本128个(占总样本的30%)。由于样地间海拔相差不大，所以本研究只考虑坡度、坡向和坡位3个立地因子。

2.2 基于树高分级的栲树树高曲线模型

基于树高分级的树高曲线模型以Chapman-Richard方程(式(1))为基础[17]，具体拟合步骤为：

y=1.3+a(1-e-bx)c。

(1)

式中：a、b、c为参数。

(1)对所有样木进行径阶整化。即有：

Dij=int(dij/2+0.5)×2。

(2)

式中：dij为第i个样地中第j株样木的胸径；Dij为第i个样地中第j株样木胸径整化后的径阶，Dij∈{6,8,…,Dmax}，其中Dmax为最大径阶。

(3)

(4)

(5)

根据以上分级，确定每株样木所属的树高级，有：

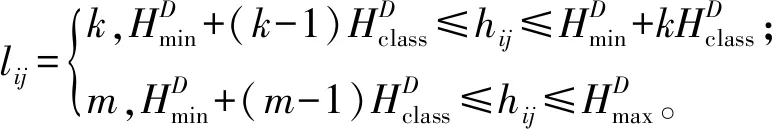
(6)

式中:lij为第i个样地中第j株样木的树高级。

(3)进入迭代程序，初始化内迭代次数t1和外迭代次数t2，令t1=0，t2=0。

(4)构建判别矩阵。对元素(Designk)ij有：

(7)

式中：(Designk)ij为第i个样地中第j株样木的判别向量(Design1×m)ij的第k个元素。

(5)改进后的Chapman-Richard方程可表达为式(8)，对式(8)进行拟合，可以获得参数a1，a2，…，am及b和c的值。

hij=1.3+(Design1×m)ijam×1(1-e-bdij)c+εij。

(8)

(6)拟合后的式(8)实际上为m条曲线方程，这m条曲线分别为分级后的m个子样本的树高曲线，然而并非所有的样本都能被其所属树高级的树高曲线准确预测，因此需计算所有样木实测树高与m条树高曲线预测树高之间的误差，并进行比较，将样木重新分级到与之误差最小的树高级中。不断修正样木树高级的过程即为内迭代过程。

lij={k|min{|1.3+ak(1-e-bdij)c-hij|，

k=1，2，…，m}};

(9)

t1=t1+1。

(10)

(8)计算样地的树高分级，并令同一样地中的所有样木的树高级等于样地树高级，不断修正样地树高级的过程,即为外迭代过程。

(11)

lij=li，t2=t2+1。

(12)

式中：li为第i个样地的树高级，ni为第i个样地中的样木株数。

2.3 基于地形分级的栲树树高曲线模型

基于地形分级的树高曲线模型通过坡度、坡向、坡位3个地形因子反映立地条件对树高曲线的影响，以此分析地形因子与树高等级的相关关系，确定地形因子的分级，并计算每个地形因子和每个树高等级对树高曲线的影响系数[17]。以下以坡向为例，说明影响系数的计算过程。

(1)首先，令

li=aspecti，

(13)

lij=li。

(14)

式中：aspecti为第i个样地的坡向等级，aspecti=1，2，…，maspect，其中maspect为坡向等级最大值。

(2)执行基于树高分级的树高曲线模拟方法的第(4)～(5)步，其中m=maspect。

(15)

(4)计算每株样木的坡向影响系数(faspect)ij。

(16)

式中：(faspect)ij为第i个样地中第j株样木的坡向影响系数。

(5)按照同样的方法计算每株样木的坡度影响系数(fslope)ij和坡位影响系数(fposition)ij，并按照下式计算每株样木的总地形影响系数(ft)ij。

(ft)ij=(faspect)ij·(fslope)ij·(fposition)ij。

(17)

(6)将(ft)ij引入式(8)即为式(18)，拟合式(18)得到参数a、b、c。

hij=1.3+(ft)ija(1-e-bdij)c+εij。

(18)

2.4 模型精度评价

用决定系数(R2)和均方根误差(RMSE)评估模型的拟合精度，用平均绝对误差(MAE)和平均相对误差(MRE)评估模型的预估精度，其定义如下：

(19)

(20)

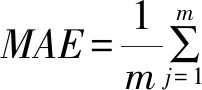
(21)

(22)

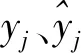
3 结果与分析

3.1 基于树高分级的栲树树高曲线模拟

分别采用经典Richard模型(模型(1))和基于树高分级的Richard模型(模型(2))进行树高曲线模拟。在模型(2)中，树高被分成5个等级，即模拟样本和检验样本分别被划分为5个子样本。

由表2模拟结果可知，模型(2)的R2相对于模型(1)有明显提高，表明基于树高分级的Richard模型较未分级的经典Richard模型有更高的拟合优度；在预估精度上，模型(2)的MAE(1.713)较模型(1)的MAE(2.101)下降了0.388，模型(2)的MRE(0.168)较模型(1)的MRE(0.204)下降了0.036，表明模型(2)有更高的预估精度。

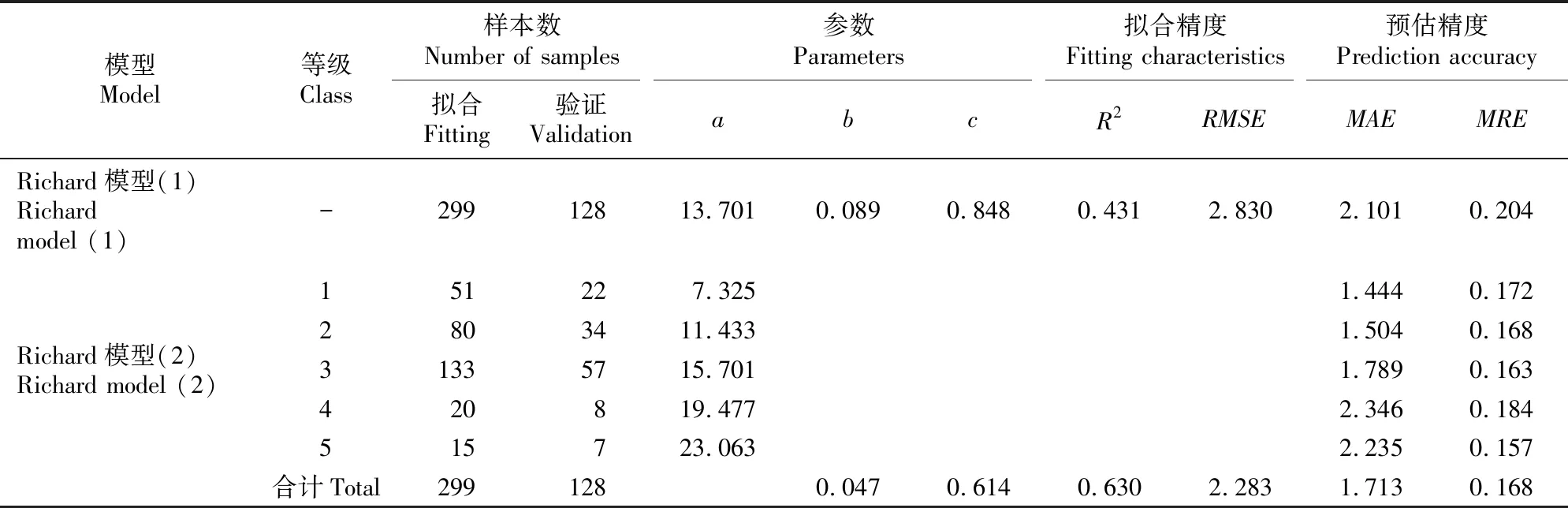
表2 模拟栲树树高的经典Richard模型(1)和基于树高分级的Richard模型(2)的拟合参数与精度

图1显示了由模型(2)生成的5个树高等级所对应的树高曲线。5条曲线对应于5个等级和子样本，可用“a+1.3”来表示各等级的树高最大生长量。从等级1到等级5，a由7.325逐渐增大到23.063，代表树高最大生长量从8.625 m增加到24.363 m。在5个等级中，MAE分布于1.444～2.346(等级4最大)，MRE分布于0.157～0.184(等级4最大)，表明与其他等级相比,等级4的预估精度较差，等级1和等级2则有较高的预估精度。

3.2 基于地形分级的栲树树高曲线模拟

按照树高的生长情况，栲树树高被划分成了5个等级，但各等级如何与实际立地因子对应起来，是需要进一步探究的问题。本研究中考虑的地形因子为坡度、坡向和坡位，参考王轶夫等[14]的研究结论，分别对3个地形因子进行分级(表3)。按照各地形因子的分级结果，构建基于坡度分级的树高曲线模型(模型(3))、基于坡向分级的树高曲线模型(模型(4))和基于坡位分级的树高曲线模型(模型(5))，各模型参数、拟合精度和预估精度如表4所示。

图1 基于树高分级的Richard模型(2)模拟的栲树分级树高曲线和验证数据分布

等级Classes坡度Slope范围Rangea+1.3f坡向Aspect范围Rangea+1.3f坡位Slope position范围Rangea+1.3f1(45,90)14.780.764北 Northern14.710.769山脊Ridge14.130.6882(35,45]15.780.815东北/西北Northeastern/northwestern14.920.780上坡Top slope14.200.6913(25,35]16.250.840东/西Eastern/western15.890.830中坡Middle slope15.490.7544(15,25]17.800.919东南/西南Southeastern/southwestern16.490.861下坡Bottom slope17.830.8695(5,15]17.840.922南Southern19.141.000山谷Valley20.531.0006[0,5]19.351.000

注：a表示模型(3)、模型(4)、模型(5)的参数，f表示各模型的地形影响系数。

Note:arepresents the parameters of model (3),model (4) and model (5),frepresents the topographic influence coefficient of each model.

由表3可知，模型(3)中6个坡度等级的(a+1.3)值为14.78～19.35，极差为4.57；相邻等级差异最大的是等级3与等级4，(a+1.3)值相差1.55，差异最小的是等级4与等级5，(a+1.3)差值为0.04。模型(4)中5个坡向等级的(a+1.3)值为14.71～19.14，极差为4.43；相邻等级差异最大的是等级4与等级5，(a+1.3)值相差2.65，差异最小的是等级1与等级2，(a+1.3)差值为0.21。模型(5)中5个坡位等级的(a+1.3)值为14.13～20.53，极差为6.40；相邻等级差异最大的是等级4与等级5，(a+1.3)值相差2.70，差异最小的为等级1与等级2，(a+1.3)差值为0.07。从(a+1.3)值的差异性看，坡位对栲树树高生长的影响最大，其次为坡度，影响最小的是坡向。

由拟合精度和预估精度(表4)可知，基于坡位分级的模型(5)的拟合精度最高，R2为0.504，RMSE为2.642；基于坡度分级的模型(3)的拟合精度最低，R2为0.440，RMSE为2.807。3个模型预估精度的比较结果与拟合精度相同。总体而言，3个基于地形因子分级的模型拟合精度和预估精度均优于不分级的经典Richard模型(1)，但却低于基于树高分级的Richard模型(2)。

根据公式(16)计算每个地形因子各等级的影响值(表3),按照公式(18)计算每株样木的总地形影响系数ft，将ft引入Richards方程(公式(19))进行曲线拟合(表5)，构建基于地形分级的树高曲线模型，即模型(6)。

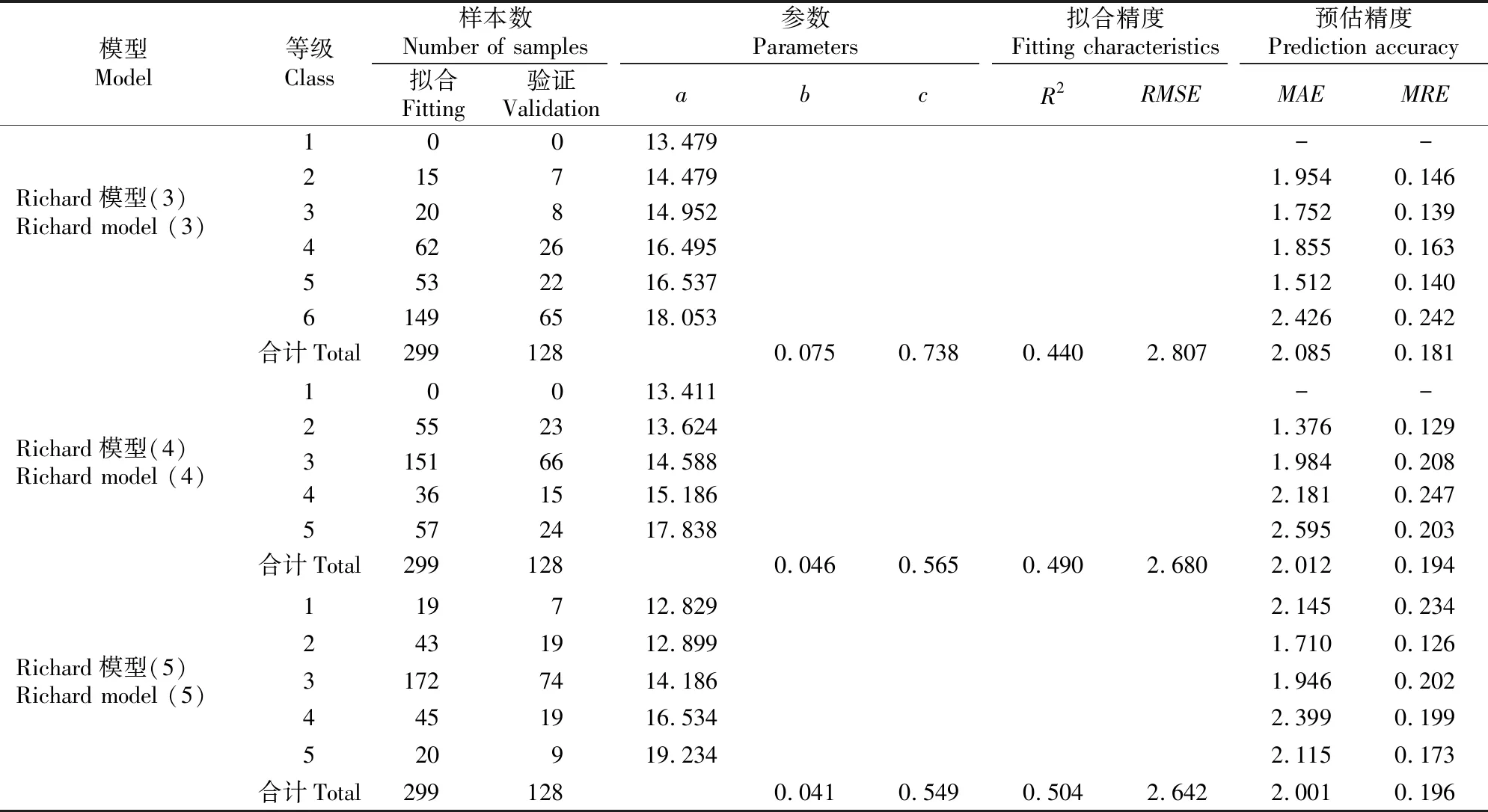
表4 基于坡度、坡向、坡位3个地形因子分级的栲树树高模型(3)、(4)、(5)的拟合参数与精度

表5 基于地形分级的栲树树高模型(6)的拟合参数与精度

由表5可知，从拟合精度上看，模型(6)的R2为0.605，低于模型(2)；RMSE为2.360，高于模型(2)，说明前者的拟合精度低于后者。从预估精度看，模型(6)的MRE为0.163，MAE为1.707，均低于模型(2)，说明前者的预估精度高于后者。再与经典Richard模型(1)相比，模型(6)的拟合精度和预估精度均较高。此外，对模型(1)、(2)、(6)的残差进行分析，结果如图2～4所示。

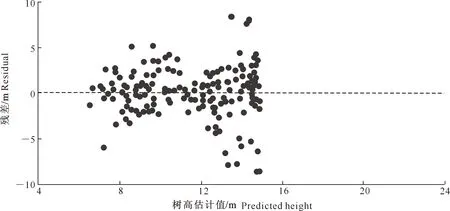
图2 基于模型(1)模拟栲树树高的残差分析

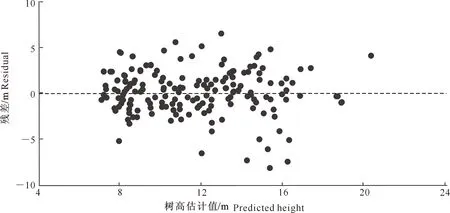
图3 基于模型(2)模拟栲树树高的残差分析

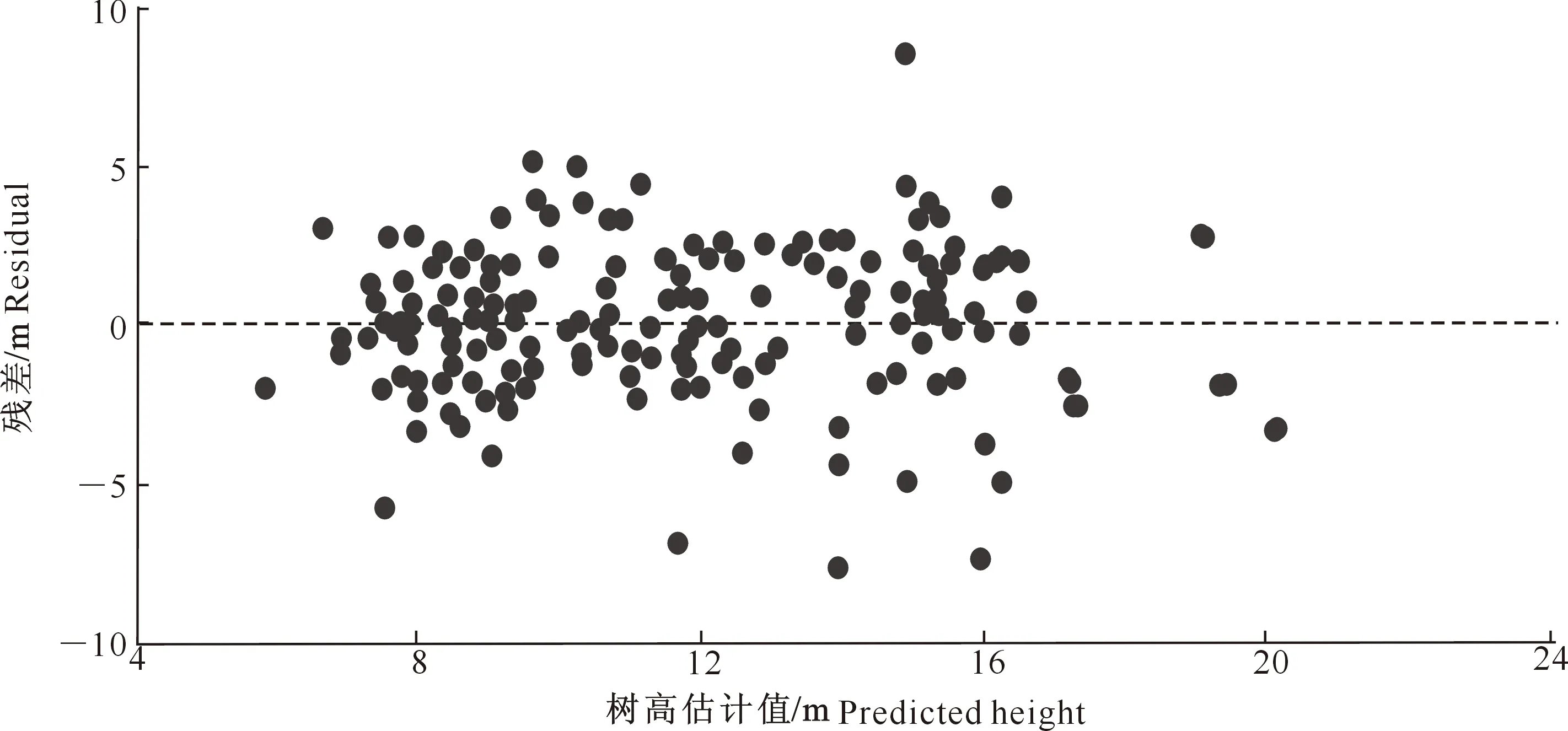
图4 基于模型(6)模拟栲树树高的残差分析

由图2～4可知，模型(1)的残差图中散点分布较为分散，并且在预测值增大时，分散程度明显加大；相对而言，模型(2)和(6)的残差图中散点的分散程度较为均匀，残差与估计值间无明显的相关关系。

不同地形影响系数所对应的树高曲线如图5所示。由图5可知，随着地形影响系数的增大，树高最大生长量逐渐增大，反映了地形因子对树高生长的影响。

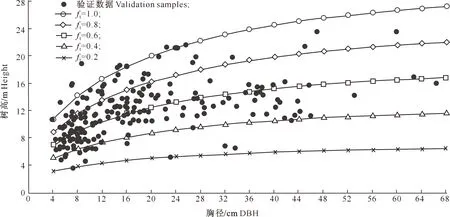
图5 基于地形分级的模型(6)模拟的栲树树高曲线和验证数据的分布

4 讨 论

本研究采用的基本方程为Richards方程，Richards方程中的参数a、b、c分别代表了树高最大生长量(曲线的渐近线)、生长速率(曲线的斜率)、生长速率的变化规律(曲线的凹凸性)。有些研究认为，环境因子的变化同时影响着树高曲线中的最大生长量参数、树种速率参数和曲线形状参数，而本研究则认为，环境因子主要影响树高曲线的最大生长量参数，树种速率参数和曲线形状参数受树木自身的遗传因素影响较大。

本研究综合考虑栲树的分布区域、立地条件、干扰程度等因素而随机设置了17个样地，能基本代表将乐地区栲树的生长状况。由于将乐地区的常绿阔叶林在1958年遭受皆伐，目前将乐地区的栲树次生林多为幼龄林和中龄林。且前期研究表明，将乐地区栲树受人为干扰严重，自然更新不佳[23]。由此导致所选取的栲树样本中小径阶样木较多，大径阶样木较少，若将本研究基于分级的将乐地区栲树树高曲线模型应用于其他地区的栲树研究，则可能需要进一步补充研究，以提高模型的精度。

本研究假设坡向、坡度和坡位对树高的影响是相互独立的，以各因子对树高生长影响系数的乘积作为总影响系数，但实际这些因子之间可能存在一定的相关性，这可能对模型的精度有一定影响，具体如何影响还有待后续进一步研究。

5 结 论

本研究以福建将乐地区常绿阔叶林中的栲树为对象，通过分析坡度、坡向和坡位3个地形因子与树高生长之间的相关关系，以Richards方程为基本方程，分别构建了基于树高分级和基于地形分级的栲树树高曲线模型，并对比分析各模型的拟合精度和预估精度。总体而言，未分级的树高曲线模型在拟合精度和预估精度中表现最差；基于树高分级的栲树树高曲线模型的R2最大，RMSE最小，表明拟合精度最高；基于地形分级的栲树树高曲线模型的MAE和MRE均最小，表明预估精度最高。

基于树高分级的树高曲线模型考虑了各类因素对树高生长的综合影响，但各类因子与树高分级之间的关系并不明确，因此这类模型还无法应用于实际树高的预估。在基于地形分级的树高曲线模型中，考虑了3个地形因子对树高生长的影响，通过地形因子与树高等级之间的相关关系确定最后的影响系数，根据地形因子的实测值确定树高曲线中的地形修正系数，提高了树高的预估精度，能够在实际生产实践中推广应用。因此，结合将乐地区实际情况，基于地形分级的栲树树高曲线模型能较为精确地预估栲树树高，这对将乐地区常绿阔叶林的经营具有一定的参考意义。