基于精确多位姿解析的水稻钵苗移栽机构研究
2019-10-10邢子勤徐亚丹俞高红武传宇
孙 良 邢子勤 徐亚丹 刘 兵 俞高红 武传宇
(1.浙江理工大学机械与自动控制学院, 杭州 310018; 2.浙江省种植装备技术重点实验室, 杭州 310018;3.杭州职业技术学院, 杭州 310018)
0 引言
水稻钵苗移栽不伤根,秧苗无缓苗期,有利于水稻低节分蘖,延长水稻生长期,提高稻米品质,实现水稻增产增收[1-6]。目前水稻钵苗移栽机构的设计方法有正向设计与逆向设计。正向设计在保证非圆齿轮凸性要求的基础上,调整机构参数,在轨迹形状符合要求的情况下判别移栽姿态是否合理[7-9]。正向设计为了兼顾合理的轨迹形状与移栽姿态,在参数的选择上存在盲目性,逆向设计在保证轨迹形状与移栽姿态的基础上,进一步考虑齿轮的凸性要求[10-12]。现有轮系式移栽机构的逆向设计主要是针对给定形状的轨迹求解机构参数并获得满足凸性要求的传动比,其求解模型中未考虑移栽臂的姿态因素。为此,本文在移栽机构的设计中采用基于精确多位姿的解析理论,在反求设计过程中对移栽轨迹与姿态进行约束,根据给定移栽轨迹的3个型值点(夹苗开始点、夹苗结束点、推苗点)的坐标和姿态,基于给定连架杆长度三位置运动生成机构综合方法,建立开链2R机构圆心点和圆点曲线方程,并求解获得不同杆长时对应圆点和圆心点的位置曲线[13-15];拟合带关键点位置信息的期望轨迹,求解基于此轨迹的开链2R机构角位移并分析其单调性,实现机构总传动比的求解与分配[16-18],获得满足凸性要求的非圆齿轮节曲线,设计七齿轮行星轮系水稻钵苗移栽机构并进行仿真与台架试验[19-21]。与贝塞尔齿轮行星轮系水稻钵苗移栽机构对比,以验证水稻钵苗的移栽质量。
1 贝塞尔行星轮系移栽机构主要问题
ZHOU等[22]利用贝塞尔曲线拟合控制点得到非圆齿轮节曲线,提出了贝塞尔齿轮行星轮系水稻钵苗移栽机构。由于贝塞尔齿轮行星轮系机构轨迹是采用贝塞尔曲线拟合获得的,而此种曲线中一个点的变化会引起整条节曲线形状的变化[23],所以较难得到理想的轨迹。图1所示为贝塞尔齿轮行星轮系水稻钵苗移栽机构的静轨迹,回程段与地面的夹角α1为80°,齿轮箱壳体运动轨迹最低点与植苗点距离S1为3 mm。
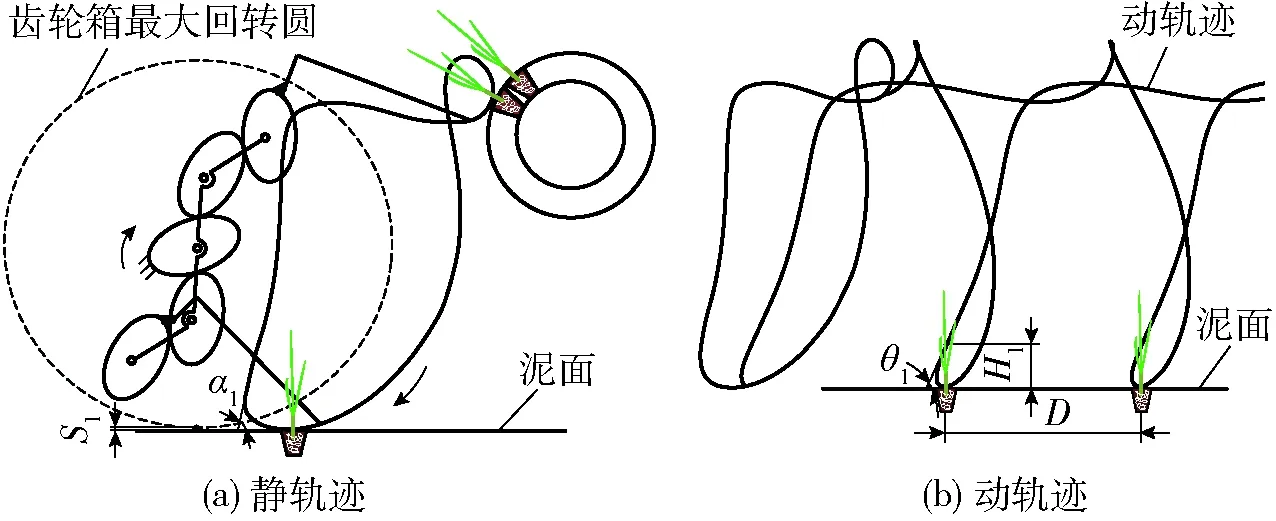
图1 贝塞尔齿轮行星轮系水稻钵苗移栽机构轨迹Fig.1 Trajectories of rice seedling transplanting mechanism with Bezier gear train
图1b所示为贝塞尔齿轮行星轮系水稻钵苗移栽机构的动轨迹,设定株距D为180 mm时,贝塞尔齿轮行星轮系水稻钵苗移栽机构动轨迹回程段与地面的夹角θ1为63°,环扣高度H1为45 mm。
贝塞尔齿轮行星轮系水稻钵苗移栽机构的静轨迹前倾,齿轮箱壳体运动轨迹最低点与植苗点距离小,动轨迹环扣高度H1为45 mm。以上原因容易引起移栽过程中秧苗翻倒及甩泥现象。
2 七齿轮行星轮系水稻钵苗移栽机构工作原理及简化
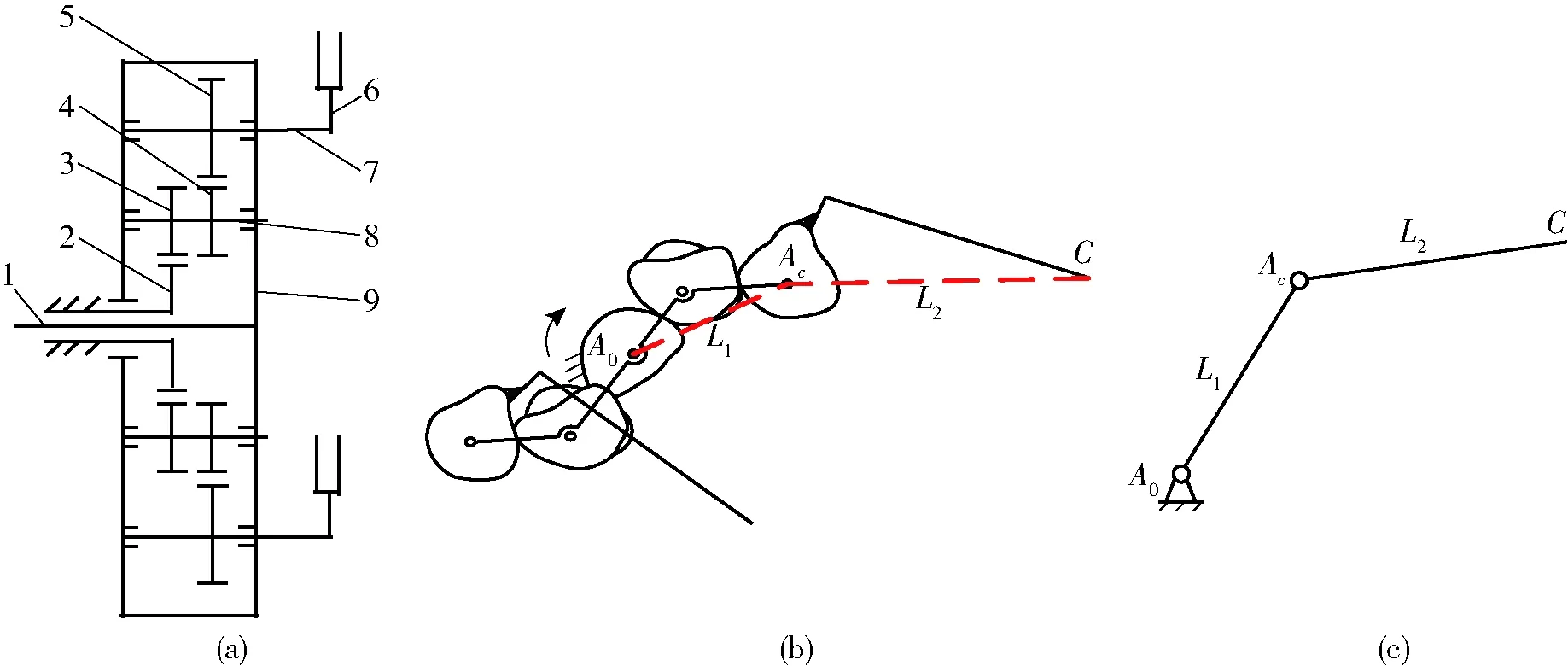
图2 七齿轮行星轮系水稻钵苗移栽机构结构简图及其简化模型Fig.2 Transplanting mechanism and simplified model of rice seedling with seven-gear planetary gear train1.中心轴 2.太阳轮 3.中间轮A 4.中间轮B 5.行星轮 6.移栽臂部件 7.行星轴 8.中间轴 9.齿轮箱
七齿轮行星轮系移栽机构由两对非圆齿轮构成,与由一对非圆齿轮构成的贝塞尔齿轮移栽机构相比,七齿轮行星轮系移栽机构可以通过更加灵活地调节传动比来控制移栽轨迹的位置以及形状。如图2所示,七齿轮水稻钵苗移栽机构主要由齿轮箱、非圆齿轮组、移栽臂等组成。移栽作业时由传动机构带动主齿轮箱转动;太阳轮固定在机架上,并与中间轮A啮合,中间轮A带动同一轴上的中间轮B转动,与中间轮B啮合的行星轮带动行星轴转动,行星轴与移栽臂固联。机构在运行时,太阳轮固定,齿轮箱匀速转动,通过内部的非圆齿轮组的传动,移栽臂一方面随齿轮箱做圆周运动,另一方面随行星轴相对于齿轮箱做周期性回转运动,从而实现复杂的轨迹与姿态要求。七齿轮行星轮系水稻钵苗移栽机构可以简化为一个开链2R机构:行星架输入记为圆心点A0,行星架输出点记为原点Ac,行星架记为杆L1,移栽臂记为杆L2,移栽臂端点记为C,如图2b所示。
3 三位姿开链2R机构综合
要求机构中的某一构件能依次通过若干个位置,用连杆机构导引构件来实现给定的位置,称为“导引机构综合”[24-27]。如图3所示,连杆平面位置由连杆平面上任意点Pi与直线PiAci的方位角来确定。
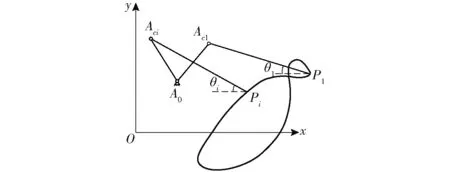
图3 刚体平面运动示意图Fig.3 Diagram of plane motion of rigid body
在第1位置时,P点坐标为P1(x1,y1),直线P1Ac1与x轴的夹角为θ1;在第i位置时,其上Pi点坐标为Pi(xi,yi),直线PiAci与x轴的夹为θi。连杆平面从位置1到位置i(i=2, 3)的位移矩阵为
(1)
其中
M11i=cosθ1iM12i=-sinθ1i
M13i=xi-x1cosθ1i+y1sinθ1i
M21i=sinθ1iM22i=cosθ1i
M23i=yi-x1sinθ1i-y1cosθ1i
M31i=0M32i=0M33i=1
其中θ1i=θi-θ1,为连杆平面第i位置相对于第1位置的转角。
如图3所示,设待求第1位置的圆心点和圆点坐标矢量分别为A0=(x0,y0)T,Ac1=(xc1,yc1)T;第i位置的圆点坐标为Aci=(xci,yci)T;则第i位置的坐标和第1位置的坐标关系表示为
(2)
根据杆长不变条件,有约束方程
[Aci-A0]T[Aci-A0]=[Ac1-A0]T[Ac1-A0]
(3)
将式(3)代入式(2),整理得
Ai1(x0xc1+y0yc1)+Ai2(y0xc1-x0yc1)+
Ai3x0+Ai4y0+Ai5xc1+Ai6yc1+Ai7=0
(4)
其中
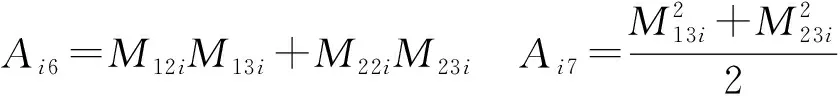
精确位姿点的个数越多,获得的轨迹越接近期望轨迹,但也增大了对非圆齿轮传动比求解凸性要求的约束条件。综合考虑,本文选取3个关键位姿点(夹苗开始点、夹苗结束点、推苗点),如图4所示。
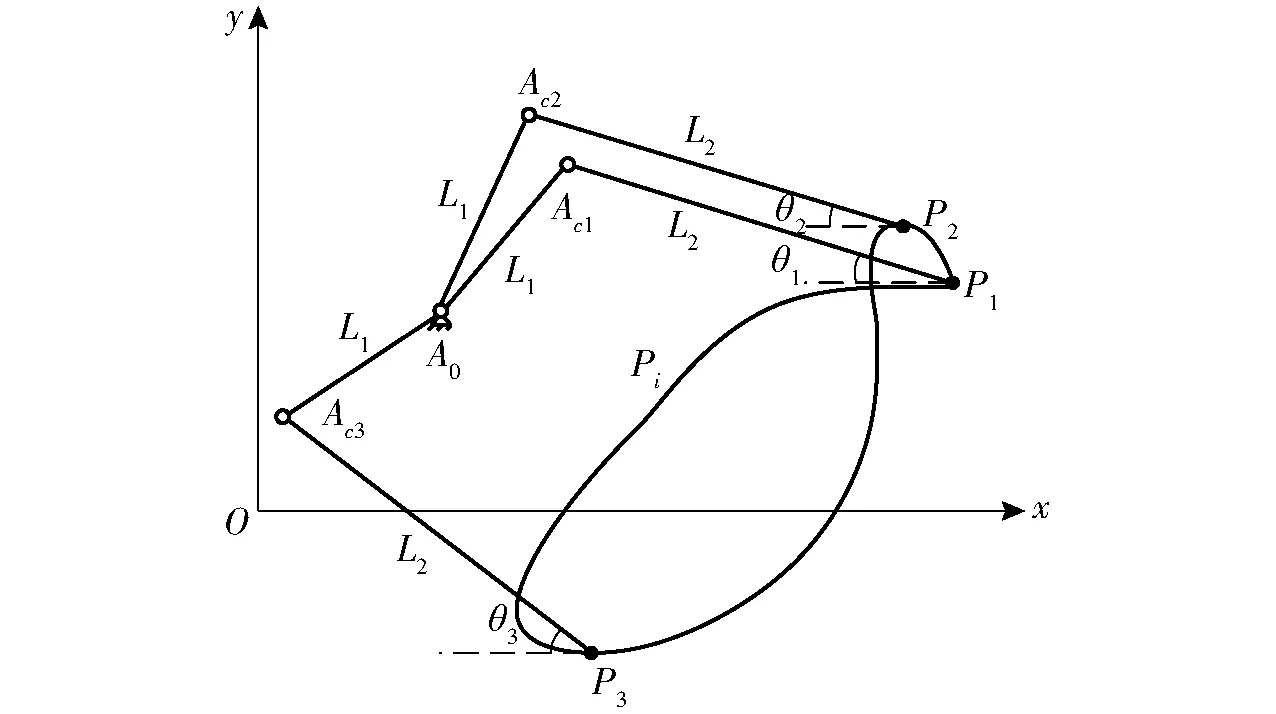
图4 移栽轨迹的3个位置Fig.4 Three positions of transplanting track
对于给定的3个位置(i=1,2,3),可以通过任意给定圆心点坐标(x0,y0)求圆点坐标(xc1,yc1),也可以通过任意给定圆点坐标(xc1,yc1)来求圆心点坐标(x0,y0)。
如果给定圆点坐标(xc1,yc1),则式(4)变为关于圆心点坐标(x0,y0)的二元一次方程组
(5)
其中
E2c=A21xc1-A22yc1+A23
F2c=A21yc1+A22xc1+A24
H2c=A25xc1+A26yc1+A27
E3c=A31xc1-A32yc1+A33
F3c=A31yc1+A32xc1+A34
H3c=A35xc1+A36yc1+A37
解方程式(5)可得圆心点坐标的表达式
(6)
限定要综合的机构的连架杆长度为r,即圆点(xc1,yc1)到与之对应的圆心点(x0,y0)的距离为r,有
(xc1-x0)2+(yc1-y0)2=r2
(7)
将式(6)代入式(7)即得圆心点(x0,y0)的分布曲线
[H20F30-H30F20-x0(E30F20-E20F30)]2+
[H20E30-H30E20-y0(E20F30-E30F20)]2=
r2(E20F30-E30F20)2
(8)
将式(8)展开,得到的是一条关于x0和y0的六次曲线[26]
(9)
其中
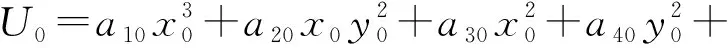
本文结合图2所述的七齿轮行星轮系水稻钵苗移栽机构简化模型与所述的三位姿开链2R机构综合方法,选定移栽轨迹的3个型值点的坐标和姿态,给定杆L1的长度,运用导引机构综合方法可以获得移栽机构行星架输入点(圆心点)与输出点(圆点)坐标曲线。
4 水稻钵苗移栽机构的尺度综合
4.1 圆点与圆心点的优选
选取移栽臂(杆L2)依次通过移栽轨迹的3个关键位置(夹苗开始点、夹苗结束点、推苗点)的坐标与姿态(图4):Xa=220.03 mm,Ya=59.74 mm,θa=30°;Xb=198.42 mm,Yb=80.01 mm,θb=37°;Xc=82.24 mm,Yc=-134.17 mm,θc=-60°。用上文所述的方法求出圆心点A0和圆点Ac的对应关系,取杆L1长度为80、85、90、95 mm时,圆点与圆心点的分布曲线如图5所示。
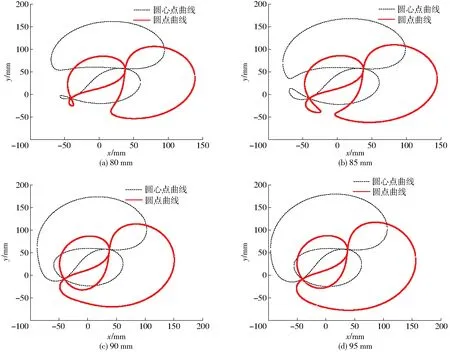
图5 不同L1杆长对应的圆点和圆心点关系曲线Fig.5 Relationship curves between dot and center point of different rod lengths L1
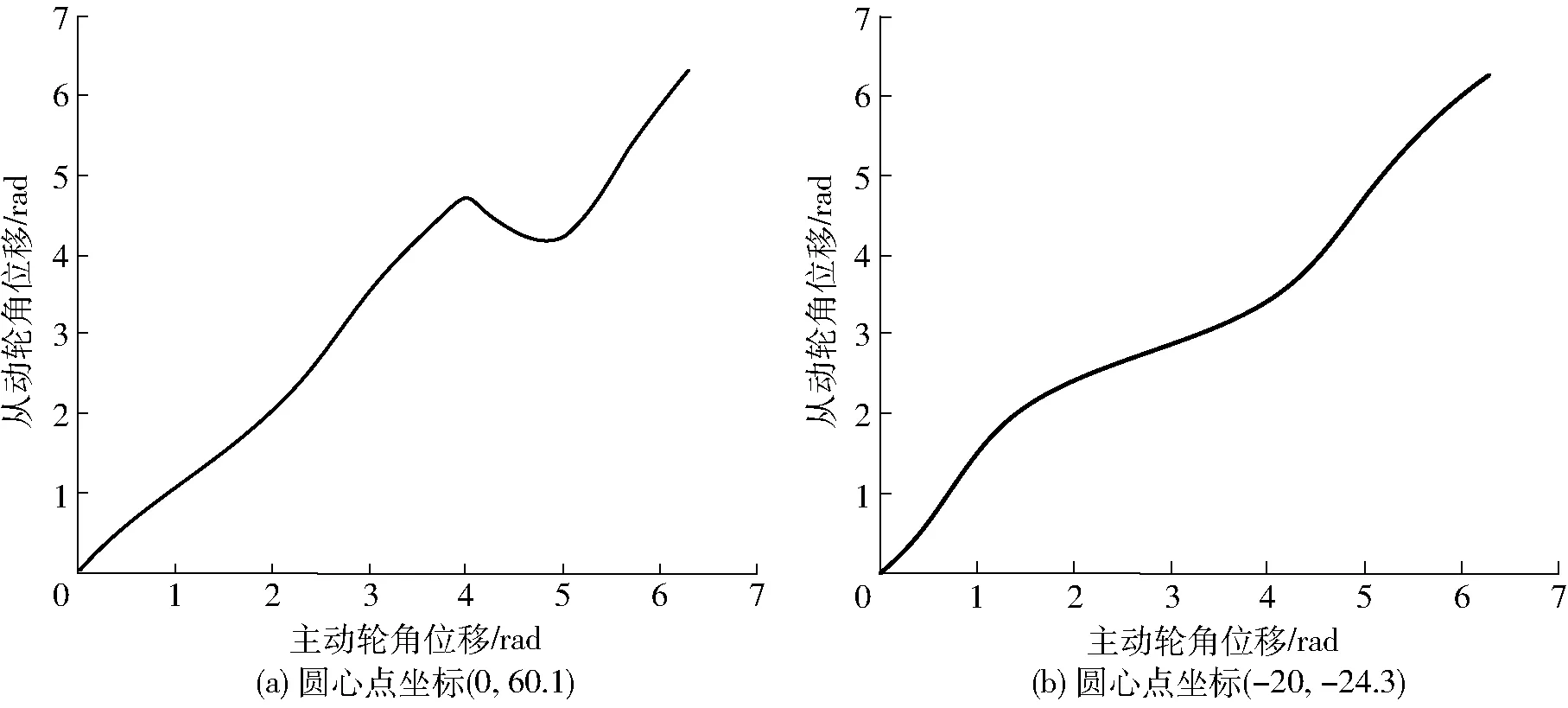
图6 从动轮角位移曲线Fig.6 Angular displacement curves of driven gear
如图5所示,在给定3位置点的情况下圆心点与圆点的曲线形状基本相同。当杆L1较长时,圆心点和圆点均形成相交的环扣。当圆心点横坐标取较大值与较小值时对应2个纵坐标,取中间值时对应4个纵坐标。因圆心点与圆点之间的距离等于杆L1的长度,所以任意一个圆心点都有对应的圆点。通过给定3位置的圆心点与圆点有很多移栽轨迹,但不是所有圆心点都满足水稻钵苗的移栽要求。如图6a所示,取圆心点坐标为(0, 60.1)时移栽机构从动轮角位移曲线出现递减的情况,说明移栽机构出现回摆现象。选取以上圆心点时移栽机构从动轮角位移会不均匀增加,导致移栽机构在运转过程中出现回摆现象,因而不能满足移栽要求。
如图6b所示,取圆心点坐标为(-20,-24.3)时,此时移栽机构从动轮的曲线单调递增,满足移栽要求。排除不合理的圆心点,在图5的曲线上将合理的圆心点标记出来,如图7所示。
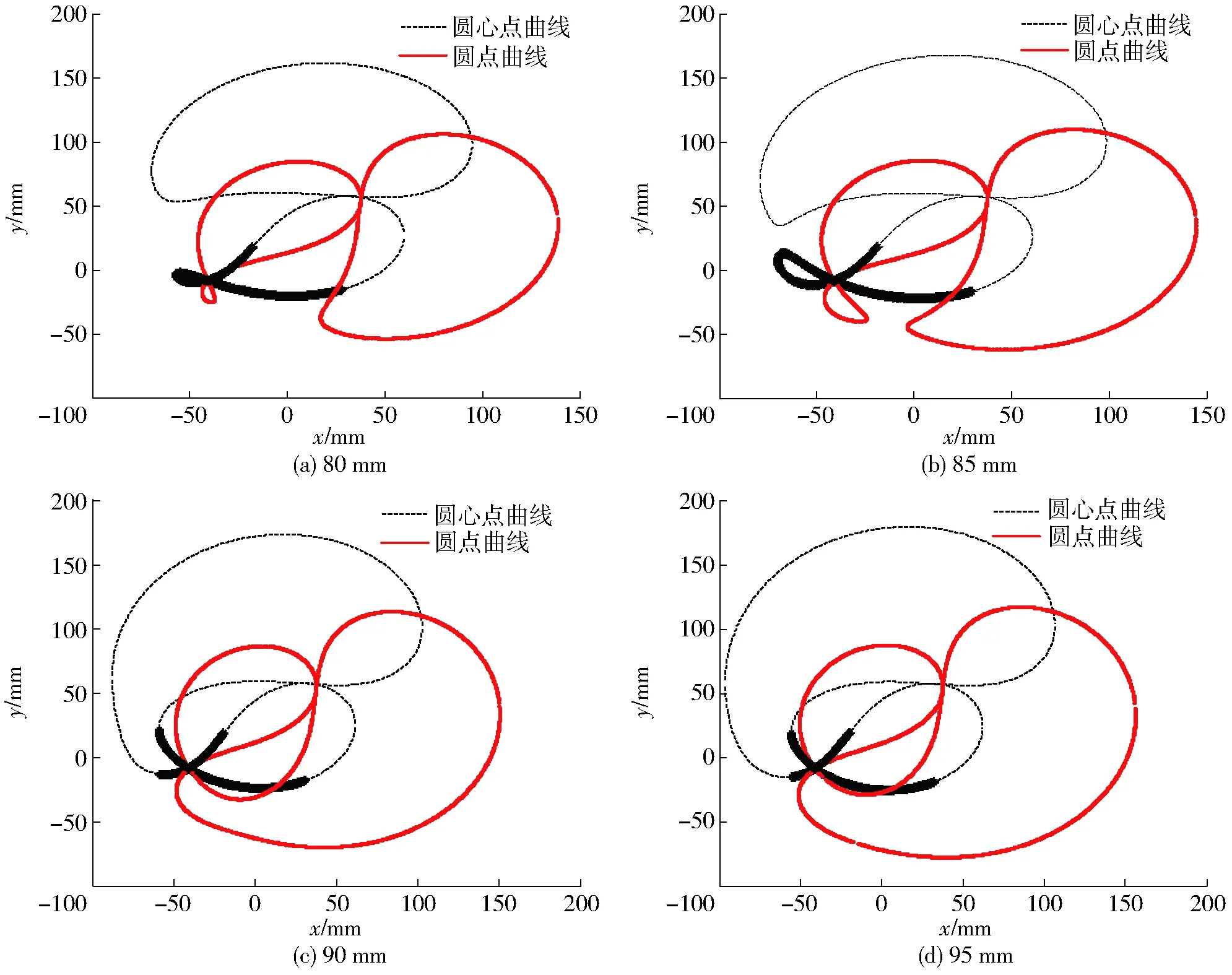
图7 不同L1杆长对应的理想的圆心点曲线Fig.7 Curves of ideal center points corresponding to different rod lengths L1
4.2 非圆齿轮的传动比求解
在3个位置点的基础上增加15个位置点共18个位置点,坐标如表1所示。
在给定机构总传动比的情况下,一级齿轮传动使齿轮节曲线的形状不满足加工要求,齿轮的中心距比较小,移栽臂之间容易发生干涉。两级非圆齿轮传动可以避免上述问题并使齿轮具有较好的加工性能。为了使两级非圆齿轮具有相似的力学和运动学性能,分配传动比时,应使两级非圆齿轮的传动比相近,本文传动比的分配方案为
式中i——机构总的传动比
i1——第1级非圆齿轮的传动比
i2——第2级非圆齿轮的传动比
k——峰谷值的调整系数
图8为第1级非圆齿轮的节曲线与传动比,图9所示为第2级非圆齿轮的节曲线与传动比。对比第1级与第2级非圆齿轮传动比曲线(图8b、9b)可以看出,两对非圆齿轮具有相近的波峰波谷以及周期,对齿轮的力学和运动学性能是有利的。

表1 拟合移栽轨迹的型值点坐标Tab.1 Fitted type points of transplanting trajectory mm
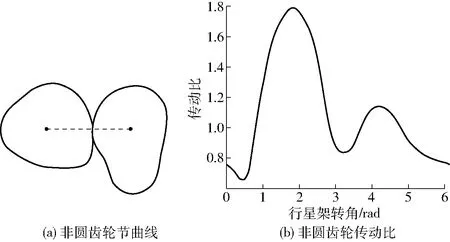
图8 第1级非圆齿轮节曲线和传动比Fig.8 First stage non-circular gear pitch curves and transmission ratio
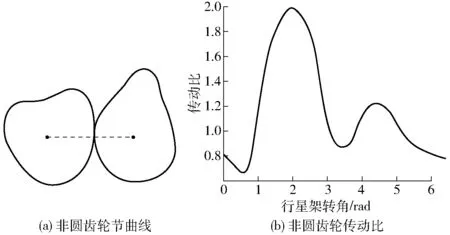
图9 第2级非圆齿轮节曲线和传动比Fig.9 Second stage non-circular gear pitch curves and transmission ratio
这种精确多位姿机构设计方法,考虑了关键点的位置和姿态信息,同时结合不等速传动比的求解与分配,对具有轨迹和移栽姿态设计要求的不等速行星轮系式机构的设计具有普遍意义。
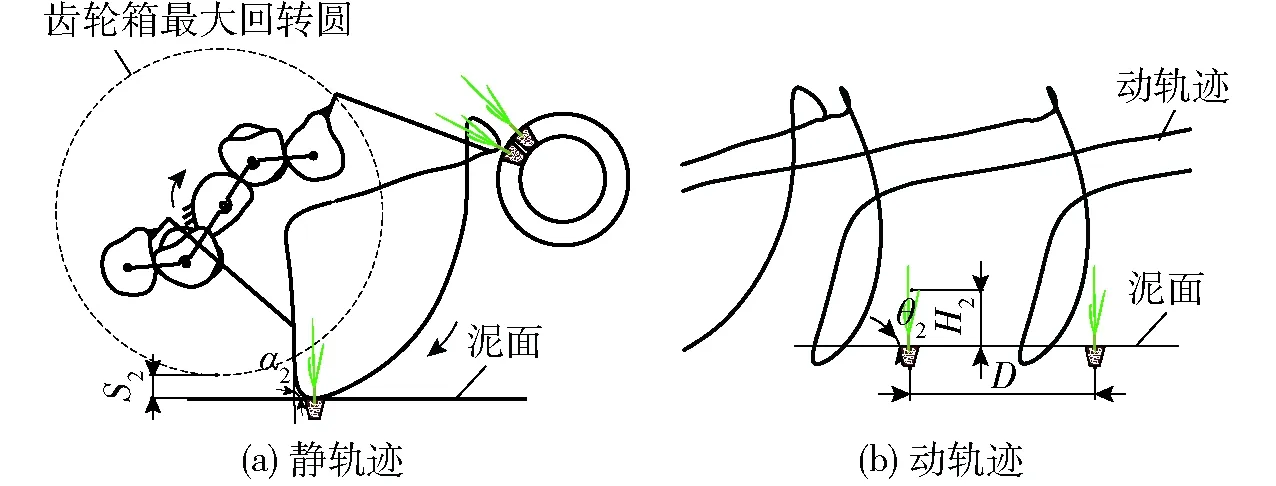
图10 七齿轮行星轮系水稻钵苗移栽机构轨迹Fig.10 Trajectory of rice seedling transplanting mechanism with seven-gear planetary gear train
5 仿真轨迹分析
选择一组优化参数(圆心点(0,0),杆L1长93.43 mm,杆L2长155 mm)进行七齿轮行星轮系水稻钵苗移栽机构设计仿真,仿真轨迹如图10所示,移栽机构的静轨迹(图10a)回程段与地面的夹角α2为90°,齿轮箱壳体运动轨迹最低点与植苗点距离S2为21 mm。
设定株距D为180 mm时,七齿轮行星轮系水稻钵苗移栽机构动轨迹(图10b)回程段与地面的夹角θ2为75°,环扣高度H2为68 mm。
6 试验验证
6.1 轨迹验证
对上述两套机构进行样机加工与试验验证。将移栽机构试验静轨迹(图11、12)与理论静轨迹(图1a、10a)作对比,可以看出试验静轨迹与理论静轨迹基本一致,并且通过试验测得移栽臂末端点经过3个关键点的姿态角分别为29°、38°和61°,验证了移栽机构物理样机的正确性。

图11 贝塞尔齿轮行星轮系水稻钵苗移栽机构静轨迹Fig.11 Static trajectory of rice seedling transplanting mechanism with Bezier gear train

图12 七齿轮行星轮系水稻钵苗移栽机构静轨迹Fig.12 Static trajectory of rice seedling transplanting mechanism with seven-gear planetary gear train
6.2 移栽试验
对七齿行星轮系水稻钵苗移栽机构进行移栽试验,试验前将水稻钵苗移栽机构安装到试验台架上,安装时移栽机构位置过低会导致移栽臂产生明显甩泥现象,所以应保证轨迹的最低点与泥面齐平。该台架由动力部分、支架、移栽机构、秧箱和土槽5部分组成,如图13所示。试验时模拟移栽机构在大田的工作状态,移栽机构在固定位置作回转运动,土槽相对移栽机构作直线运动。试验采用14×29钵盘,钵苗培育时间为30 d左右,钵苗茎秆高度在12 cm左右。
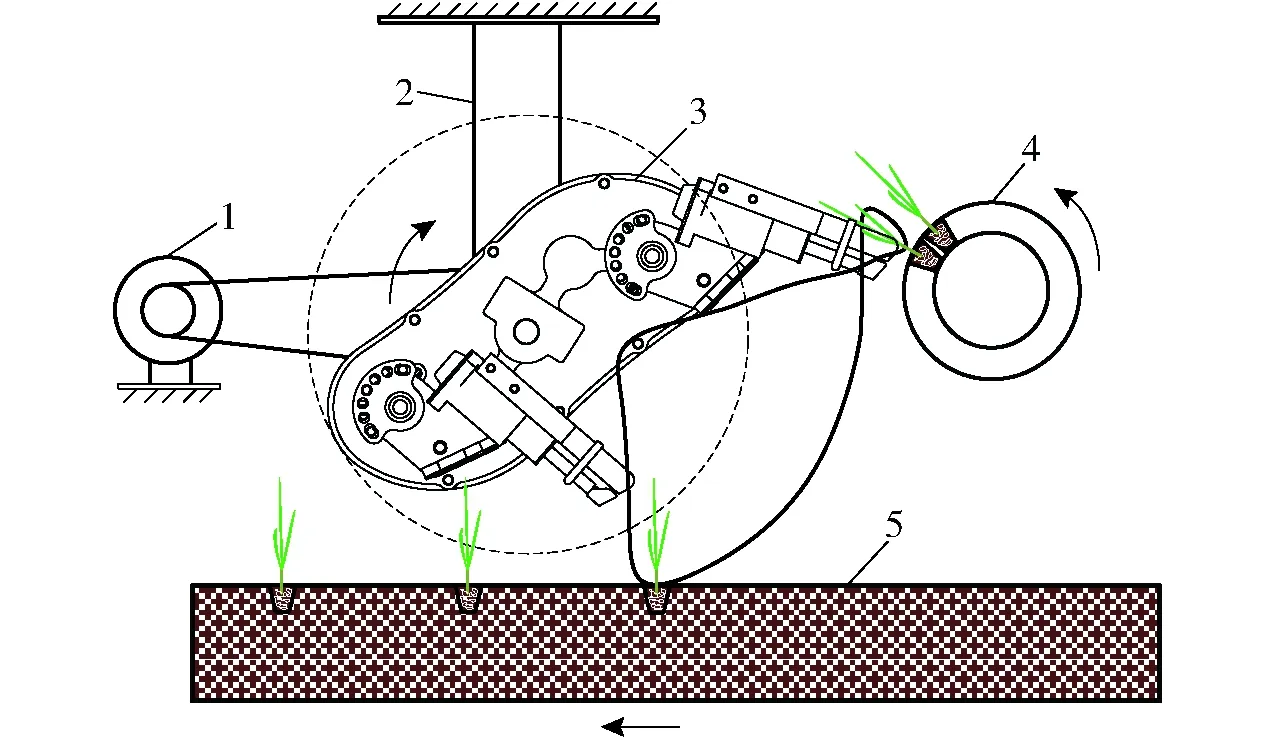
图13 试验台架示意图Fig.13 Test bench1.动力部分 2.支架 3.移栽机构 4.秧箱 5.土槽
将钵苗分成40组进行试验,每组5株苗,共移栽200株。对倒伏的钵苗进行计数并测得新移栽机构翻倒率为2.5%,原移栽机构翻倒率为18.4%。对比图14与图15可以看出,七齿轮行星轮系水稻钵苗移栽机构进行移栽作业时水稻秧苗直立度较好,翻倒现象得到改善,无明显甩泥现象。

图14 七齿轮行星轮系水稻钵苗移栽机构移栽试验Fig.14 Transplanting experiment of rice seedling transplanting mechanism with seven-gear planetary gear train

图15 贝塞尔齿轮行星轮系水稻钵苗移栽机构移栽试验Fig.15 Transplanting experiment of rice seedling transplanting mechanism with Bezier gear train
7 结论
(1)选定移栽轨迹的3个型值点(夹苗开始点、夹苗结束点、推苗点)的坐标和姿态,运用导引机构综合方法获得给定位姿下的移栽机构行星架输入点(圆心点)与输出点(圆点)位置,结合B样条拟合方式获得移栽臂输出角位移单调变化的移栽轨迹,最终获得满足移栽要求的圆心点与圆点的曲线。选择合适圆心点与圆点坐标设计七齿水稻钵苗移栽机构,并进行虚拟仿真、样机加工与台架试验。
(2)两套移栽机构的试验静轨迹与理论静轨迹基本一致,验证了物理样机的正确性。与贝塞尔齿轮行星轮系水稻钵苗移栽机构的作业轨迹相比,本文研究的移栽机构轨迹回程段与地面夹角增加,齿轮箱回转半径最低点与推苗点距离增加,环扣高度增加。
(3)模拟移栽机构在大田的工作状态,对七齿行星轮系水稻钵苗移栽机构进行移栽试验,试验时水稻秧苗直立度较好,在移栽过程中秧苗翻倒率低,甩泥现象得到改善,有利于提高水稻钵苗的移栽质量。
