电子商务物流延误风险在节点间的传播研究

乔鹏亮 闫政维

服务电子商务的物流活动在具体运行过程中面临着众多风险因素，其中延误风险是造成物流效率低下和消费者投诉的关键因素之一，以贝叶斯理论为基础构建了电子商务物流延误的风险传播网络模型，并以北京和广州到钦州为例，以三种随机事情导致的物流风险为例进行了实证分析，讨论了物流延误风险传播的三种效应，对于物流风险延误传播的分析有助于科学决策，论文最后提出了基于科学预测的管理建议。

随着电子商务的迅速发展，网上购物已经成为生活方式的一种，服务电子商务的物流效率也一直在进步，甚至在2018年“双11”最快的货物到达买家手里只用了十几分钟，物流的进步使得网络购物的便利性得到最大限度的发挥。虽然服务电子商务的物流一直在进步中，但是由于物流环节众多，各结节间商家的协作等问题，物流延误的投诉竟然增多了，据国家邮政局数据统计，2018年7月快递延误消费者投诉次数达26074次，而一年前2017年8月的快递物流延误消费者投诉次数为2778次，一年间电子商务物流延误投诉增长将近10倍。由此可见，电子商务的物流延误不但没有因技术的进步而减少，反而不断增加，因此，探索电子商务物流延误问题就具有十分重要的现实意义。

一、文献综述

时间延误最初在生产制造领域被广泛讨论，近年来逐渐延伸到对供应链的管理中，在物流领域，由于研究的和合作节点比供应链窄，研究少一些，以“物流”和“延误”为关键词检索的文献并不多，少量的文献也围绕多节点的物流活动展开，如国际物流网络合作中的业务协作和延误引起的可靠性等。国内在延误方面的研究主要集中在航空运输的飞行延误方面，在延误的模型化研究方面，通过以“物流延误”为关键词进行搜索，国内的文献出现2篇报道（2014、2016），学术方面只有1篇关于物流节的网络订单延误的原因分析，研究的内容是关于定性方面的现象分析，没有模型化的分析内容。

二、电商物流延迟风险传播模型

（一）物流延误传播的概念

当物流配送开始时，假设货物从A点出发，经过B点，最终到达C点，A点到B点正常需要3天，B点到C点需要2天，总共需要5天时间，当发生延误时，这时候可能会出现：一是A到B也发生了延误，使得天数4天，但是B到C时却用了1天，总共时间刚好5天，没有发生延误;二是A到B没有发生延误却提前了，用了2天，但是B到C是却用了3天，发生延误，但是总共用了5天，没有产生延误;三是A到B发生延误，用了4天，B到C也發生延误，用了3天，总共时间用了7天，发生了延误;四是A到B没有延误，B到C也没有延误，总共时间也没有发生延误，以上说明了物流延误在传播中受不同因素影响，并且在受影响下所传播至下个点是否对延误效果有增强、减小或者不变。另外在配送过程中，当货物配送到快要达到下个配送点时，配送点有需要装卸货物并且有需要出发的车辆，这时候如果路程中发生了延误，配送点有两种情况，第一是配送点等待延误的货物，那么货物得到了快速装卸的机会，但是也影响了到达另外一个配送点的配送时间，使得配送点的配送时间延误总和增加;第二是配送点到时发车，没有等待延误车辆，总的配送时间会减少，但是会影响货物的装卸时间，造成装卸货物的延误。所以说延误是不可能随着时间消失的，况且在现实中具有不确定性。

（二）基于贝叶斯网络的物流风险传播关系

贝叶斯网络（BN）就是在概率推理下的一种图形化的概率网络，同时也是一个二元组，从二元组来看，就是BN=（G，P），G=（V，E），从图形来看就是一个有向无环图，结合二元组，字母V代表着节点集，一个节点集就对应着相关领域的某一随机变量;字母E代表着有向边集，两者变量之间有着相互依赖的关系，即因果关系。现实中的物流风险正是在紧邻的上下游之间传播，下游的风险概率直接受到上游风险概率的影响，因此，利用贝叶斯网络可以较为准确地刻画物流风险在物流节点间的传播问题。基于此，本文选择以贝叶斯网络为基础，以北京、武汉、广州、南宁为物流节点，以现实的购物时间延误为案例，开展基于电子商务物延迟风险传播的研究。

三、物流风险传播算例

（一）算例背景

在建立延误模型时，选取北京至南宁物流配送的延误、广州至南宁物流配送的延误、南宁至钦州物流配送的延误为其相应的变量（节点），节点意义为：当北京（B）或者广州（G）物流配送点发生延误时，可能会导致到达南宁（N）的时间发生延误，实际情况是现实路途中发生延误时在过程中可能减小了，对南宁没有太大影响，或者至南宁的物流延误没有减小，直接传播至钦州（Q）;当传至钦州时，实际情况可能为一是南宁受延误影响，到达钦州时整体时间没有延误，为此北京至钦州没有延误，二是南宁受延误影响不大，但是到达钦州时总体时间却发生了延误;三是南宁受延误影响大，传至钦州时，整体时间也发生了延误。同理，同样选择北京至武汉（W）的配送延误，武汉至柳州（L）的配送延误，南宁到柳州的配送延误为相应的变量，节点意义为当北京配送至武汉时发生延误，导致武汉至柳州有三种情况，一是武汉至柳州时间提前，但是总体时间发生了延误;二是武汉至柳州时间没有延误，总体时间没有发生了延误;三是武汉至柳州发生了延误，总体时间也发生了延误。为此每个节点取值均是大于等于7或小于7，各变量对应的值域为BQ：{<7，≥7};GQ：{<7，≥7};NQ：{<7，≥7};BL：{<7，≥7};WL：{<7，≥7};NL：{<7，≥7}。

（二）延误模型的网络结构

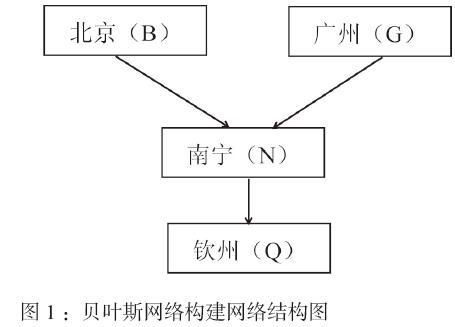
根据上述模型变量之间的相互关系，在构造贝叶斯网络结构上，首先是确定相关变量集及其对应的值域;其次是给出网络结构，确定有向无环图;然后是给出各个因素局部概率的分布情况，即条件概率，表示节点间与父节点之间的相互关系;最后根据贝叶斯网络构建网络结构图，如下图所示：

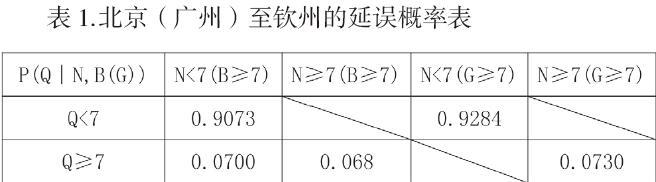
每一个节点表示了一个变量，节点之间的有向弧则表示了各节点（变量）之间的关系，即因果关系。参考了国家邮政局公布的2017年主要快递企业有效申诉表，根据国家邮政局监测提供的数据，以邮政快递为准接下来计算北京（B）到钦州（Q）的条件概率：

北京到南宁快递是3天，南宁到钦州是2天，共5天，当强冷空气南下，北京至南宁的航班受延误导致5天才到，这时候有3种情况，一种是南宁到钦州1天到，共6天，這种是没有发生延误;一种是南宁到钦州2天到，共7天，这时产生了延误;最后一种就是南宁到钦州变成了3天，也发生延误了。

因此根据贝叶斯公式计算出第一种情况;

P（N<7∣B≥7）=0.0736*0.9282/0.0718=0.9515

P（Q<7∣N<7）=0.9301*0.9282/0.9515=0.9073

第二种情况;

P（N<7∣B≥7）=0.9515

P（Q≥7∣N<7）=0.9274*0.0718/0.9515=0.0700

第三种情况;

P（N≥7∣B≥7）=0.0763*0.0718/0.0718=0.0763

P（Q≥7∣N≥7）=0.0723*0.0718/0.0763=0.0680

北京至武汉的快递是3天，武汉至柳州的快递是2两天，共5天，当出现暴雪天气时，北京至武汉的航班受延误，根据实际情况，可以得知有3种情况，一是北京至武汉发生了延误，用了5天，武汉至柳州时提前了一天，总共时间6天，没有发生延误;二是武汉到柳州用了2天到，没有发生延误，但是总共花了7天，这时产生了延误;最后一种就是武汉到柳州变成了3天，发生延误了，总体时间也发生了延误。这时需要考虑一种情况，假设武汉跟南宁是相互关系的。然后在贝叶斯公式基础上计算。

同理，北京到南宁快递是3天，南宁到柳州是2天，共5天，当强冷空气难下，北京至南宁的航班受延误导致5天才到，这时候有3种情况，一种是南宁到柳州1天到，共6天，这种是没有发生延误;一种是南宁到柳州2天到，共7天，这时产生了延误;最后一种就是南宁到柳州变成了3天，也发生延误了。

P（N<7∣B≥7）=0.0736*0.9282/0.0718=0.9515

当武汉没有发生延误时：

P（L<7∣N<7，W<7）=

0.9290*0.9282*0.9188/0.9515*0.9314=0.8940

当武汉发生延误时：

P（L<7∣N<7，W≥7）=

0.9290*0.9282*0.0731/0.9515*0.0727=0.9112

其他情况;

P（N<7∣B≥7）=0.9515

当武汉没有发生延误时：

P（L≥7∣N<7，W<7）=

0.9279*0.0718*0.9397/0.9515*0.9314=0.0706

当武汉发生延误时：

P（L≥7∣N<7，W≥7）=

0.9279*0.0718*0.0771/0.9515*0.0723=0.0747

第三种情况;

P（N≥7∣B≥7）=0.0763*0.0718/0.0718=0.0763

当武汉没有发生延误时：

P（L≥7∣N≥7，W<7） =

0.0751*0.0718*0.9325/0.0763*0.9307=0.0708

当武汉发生延误时：

P（L≥7∣N≥7，W≥7）=

0.0751*0.0718*0.0762/0.0763*0.0747=0.0732

（三）模型结果

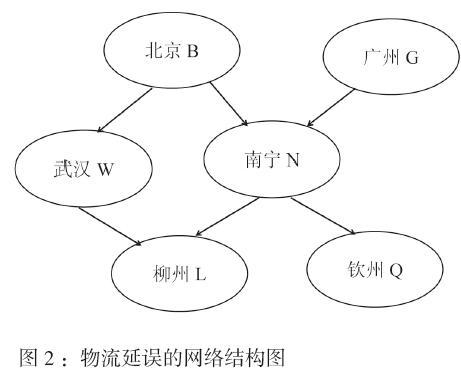
根据以上分析，当北京发生延误时，对于武汉来讲，出现以下3种情况，当延误传到武汉时，一是在武汉延误被降低了，这时候要考虑南宁的延误情况，当武汉没有发生延误，南宁也没有延误时，柳州没有延误的概率为0.9338，当武汉没有发生延误，南宁有延误时，概率为0.9408;二是当延误传至武汉时，武汉到柳州的快递没有发生延误，但是对于柳州来讲，总体时间产生了延误，此时当武汉没有发生延误，南宁没有延误时，柳州发生延误概率为0.0729，当武汉没有发生延误，南宁发生延误时，柳州出现延误的概率为0.0752;最后一种情况，就是北京的延误传至武汉时，武汉对延误的吸收能力有限，将延误传播至柳州，这样总体上都产生了延误，这时当武汉发生延误，南宁没有延误时柳州发生延误的概率为0.0732，当武汉发生延误，南宁也发生延误时，这时柳州发生延误的概率为0.0720。同样，当南宁发生延误时，对于柳州来讲也有3种情况，一种就是延误到南宁后延误效应影响不大，南宁到柳州的快递没有发生延误，这种情况下当南宁没有发生延误，武汉没有发生延误下柳州也没有发生延误的概率为0.8940，在南宁没有发生延误，武汉发生延误下柳州没有发生延误的概率为0.9112;第二种情况就是南宁至柳州没有发生延误，但是总体时间却发生了延误，同样的当南宁没有发生延误，武汉没有发生延误下柳州发生延误的概率为0.0706，当南宁没有发生延误，武汉发生概率时柳州也发生延误的概率为0.0747;第三种就是北京的延误传至南宁，导致南宁到柳州也发生了延误，这时候当南宁发生延误时，武汉没有发生延误的概率下柳州发生延误的概率为0.0708，当南宁发生延误，武汉也发生延误下柳州发生延误的概率为0.0732。

为此建立如图以下网络结构：

四、结论及建议

1.物流延误受到随机因素的干扰，具有不确定性。物流延误的初始延误点事件具有随机性，在进行实践过程中要进行线路和物流线路上的历史数据统计，从大数据中分析出事件出现的频率等，归纳分类各类事件出现的具体情况，并从中探索随机因素导致的延误事件发生普遍规律，从而方便进行科学管理，对于出现概率高、影响范围广的随机因素要进行前置监控和预测，将不确定性用科学的方法进行管理，提高决策的科学性。

2.物流延误是可以被合理预测到的，根据预测结果判断延误出现的可能，能够对提高整个物流环节效率管理，提升物流服务效率，提高社会经济利用水平，降低重复和消除浪费。在预测中，要从初始节点物流事件出发，采用大数据、概率论等相关手段，在延误发生之后要加强信息沟通，为科学预测提供基础保障，并在物流节点间实施动态监控，对传播的三种效应进行不断跟踪，为决策提供可靠的信息依据。（作者单位：1.广西科技大学  北部湾大学; 2.广西科技大学）

本文系：广西科技厅课题（中国-马来西亚物流科技人才交流创新平台建设2017AD19022）;教育部人文社科课题（海上丝绸之路跨境电子商务物流风险防范机制研究15XJA630005）。