一种基于危险度的电网连锁跳闸分析方法
2019-10-09
(福建工程学院 信息科学与工程学院,福建 福州 350118)
自1965年美国纽约大停电以来,世界上还有不少地区也发生过大停电事故,且多半是由连锁故障引起的。研究者们从多个角度对电网的连锁故障问题进行了分析:如文献[1]引入熵的概念,利用潮流熵分析电网潮流水平对电网连锁故障的影响;文献[2]将熵引入风险领域,研究了电网在连锁故障冲击上的脆弱性问题;文献[3]研究了电网的小世界网络结构及其对连锁故障传播的作用;文献[4]研究了电网在连锁故障作用下的脆弱性等等。
电网在连锁故障的最初发展阶段通常表现为连锁跳闸,具体形式是:当发生初始故障的支路被切除后,因电网的运行状态重新调整,其余的某些支路可能会被诸如距离Ⅲ段一类的后备保护切除,这是第二级故障;进一步,电网的运行状态将再次发生调整,可能引起新的跳闸,依次类推。
实际运行的电力系统运行状态经常发生改变,当其受到初始故障冲击时,其实际运行状态与发生连锁故障的边界运行状态之间有多远的距离?如何分析这种距离?回答这些问题对避免连锁跳闸事故显然具有十分重要的意义。
为此,本文分析了连锁跳闸的临界运行状态,并以危险度指标的形式提出评价电网临界状态与当前运行状态之间距离的表达形式,在此基础上以危险度指标为目标函数,考虑电网各种电气约束条件,建立危险度优化计算的模型,结合遗传算法实现完整的计算流程,最后通过IEEE-39系统,对算法进一步分析和验证。
1 电网连锁跳闸的临界状态
正常运行的电网若发生了初始故障,当故障支路被切除后,电网是否发生连锁跳闸取决于电网潮流重新分布后各支路的电气量是否进入后备保护的动作区内。若电网各支路配置的后备保护为距离Ⅲ段保护,则电网的潮流重新调整后,是否发生连锁跳闸取决于各支路的测量阻抗和后备保护的具体配置。本文只针对电网支路配置了距离Ⅲ段后备保护的情形展开研究。
根据实际电网连锁跳闸的表现,当电网中第i条支路Li因初始故障而发生停运时,经过其后的电网重新调整,除支路Li外,其他任一支路Lj是否发生连锁跳闸可采用式(1)评判。
Zj·dist=|Zj·lim|-|Zj|
(1)
式中,Zj·dist为衡量Zj·lim和Zj之间距离的量,而Zj·lim和Zj是与支路Lj上配置的距离Ⅲ段保护有关的阻抗电气量,其表达形式和具体取值跟距离保护的动作特性有关[5-6]。例如,若支路Lj配置了具有偏移圆特性的距离Ⅲ段保护,则参照文献[7]所给出的保护动作方程,则Zj·lim和Zj的表达形式如式(2)所示。
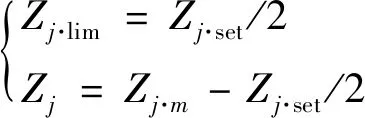
(2)
式中,Zj·set/2为支路Lj所配置距离Ⅲ段保护的整定值,Zj·m为支路Lj上的测量阻抗。
由式(1)及连锁跳闸的概念可知,当Zj·dist>0时,支路Lj不会发生连锁跳闸,而当Zj·dist≤0时,支路Lj由后备保护予以切除。
设电网的支路共有l条,则利用式(1)推出式(3)所示的矩阵J:

(3)
根据连锁跳闸的实际表现,可知当初始故障前电网的状态为临界状态时,J的行列式必定等于零,即有式(4)成立。
|J|=0
(4)
同时对每一条支路来说,还应有式(5):
g=min(Zi·dist)≥0,i≠j,i=1,2,···,l
(5)
2 电网发生连锁跳闸的危险度描述
当正常运行的电网受到初始故障冲击时,若发生了连锁跳闸,说明初始故障发生前的电网处一种危险的运行状态。这个结论是显而易见的,本文暂不予以讨论。本文分析的情形是,当电网受到初始故障冲击时,不会发生连锁跳闸的情形。在这种情形中,电网在发生初始故障前的运行状态与临界状态之间的距离越近越危险。以双节点系统为例对危险距离进行说明,电气接线图如图1所示。
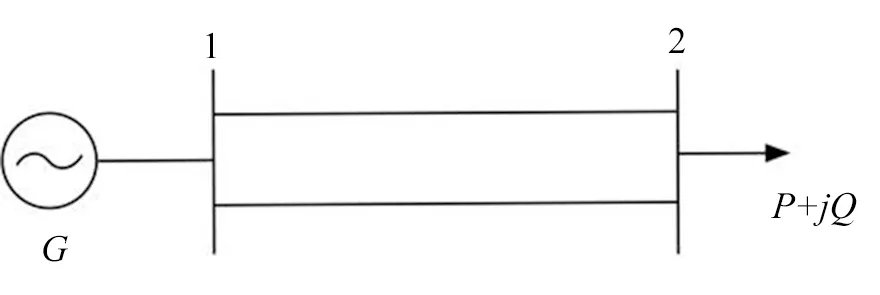
图1 2-节点系统的电气接线图Fig.1 Electrical wiring diagram of a 2-node system
图1所示节点1为发电机母线,为该系统的平衡节点,节点2为负荷节点,即为PQ节点。当图1所示系统其中一回线路因故障退出运行,那么另一回线路可能会因过负荷使该线路的距离Ⅲ段保护动作退出运行,其保护动作的临界状态即为危险状态,该状态与初始故障发生后瞬时状态的最短抽象距离即为危险距离,该系统的危险距离可用图2来说明。
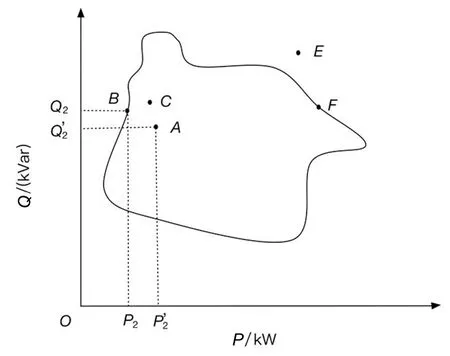
图2 2-节点系统的连锁故障临界状况Fig.2 Critical state of cascading failure in the 2-node system
横轴和纵轴分别为节点2的有功和无功注入功率值,若另一条线路跳闸,则发生了二次跳闸,即连锁跳闸故障。图2所示的封闭环上为发生跳闸故障的临界状况,则环内部为系统的正常运行状况,环外部为系统已发生连锁跳闸的运行状况。不妨设A点为正常运行时的位置,B点和F点表示初始故障发生后,发生二次跳闸的临界位置,C点代表的系统在初始故障发生一段时间后暂时没有发生二次跳闸,E点则发生了连锁跳闸。若在更多节点的系统中,范围外类似E点的状况则发生了二次跳闸,甚至更高次跳闸。
图1所示节点2为PQ节点,考虑初始故障瞬时潮流不会瞬间转移,此时系统的已知节点的注入功率与正常运行时相同,那么初始故障发生后的瞬时状况在A处,节点2对应的节点注入有功功率和无功功率分别为P′和Q′。为研究该系统当前潜在的最大危险,考虑最严重的情况。
虽然B点和F点均处于临界状况,但B点距离A点更近,不妨认为B点是临界状况圈中距离A点最近的点,在临界状况点B时,该节点的注入有功功率和无功功率则分别为P和Q,那么该系统在发生初始故障后的瞬时运行状况与临界状况的最短距离可由式(6)表示:
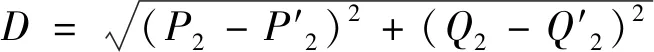
(6)
D的值就是这2-节点系统连锁跳闸的危险距离。将这个理论推广到N个节点的系统,并将该系统所有的已知节点的注入功率考虑在内,可表示为:
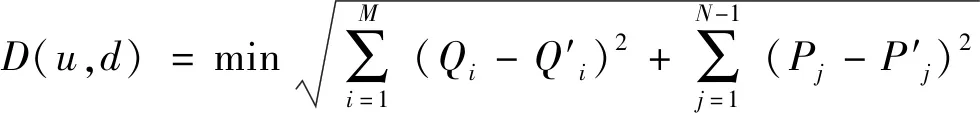
(7)
式中,u表示控制变量,d表示扰动变量,控制变量与扰动变量之差即为节点注入功率,包括有功注入功率和无功注入功率。N为系统网络的节点数,M为PQ节点的数目,有一个平衡节点,所以已知节点的有功注入功率P的个数为N-1,已知节点的无功注入功率Q的个数为M。P′和Q′为初始故障发生后瞬间的节点注入功率,视故障支路退出运行瞬间潮流不进行转移。P和Q为临界状况下任一点的注入功率。
3 考虑连锁跳闸的电网危险度指标及模型
定义D(u,d)为危险距离函数,其自由变量为状况变量,相应的危险度定义为:
E(u,d)=1/D(u,d)
(8)
式(8)表明,危险距离越小则连锁跳闸的危险度越大。联系第一节所述连锁跳闸的危险度描述,可以建立连锁跳闸临界状态的数学模型:

(9)
式(9)表明,在初始故障线路切除后,系统的潮流自行调整,若某一支路刚好过载,其对应保护被触发,此时临界状况矩阵J的对角线元素刚好存在0元素,说明系统处在连锁跳闸的临界状况下。再考虑电力系统正常运行的固有约束条件,其等式约束和不等式约束表示为

(10)
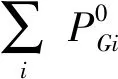
初始故障支路Li切除后,电网的等式约束方程为:
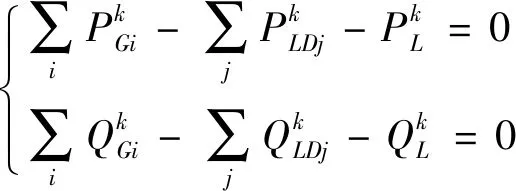
(11)
式(11)等式约束的条件含义同电网正常运行时的等式约束,角标k表明初始故障已发生。系统在发生初始故障后可能处于紧急状态,其不等式约束则不能满足。将式(7)-(11)综合起来,即可构成考虑连锁跳闸的电网运行危险度的数学分析模型:
式中的D(u,d)即为危险距离,危险距离越大,危险度越小。对危险度进行优化计算即寻求危险距离的最小值。
4 基于简单遗传算法计算危险度
式(12)所示危险模型中,第一个式子即为优化目标函数,即危险距离最小。将式(12)所示为约束部分,采用基本遗传算法进行求解危险距离的最小值。
确定一个规模为popsize的种群population,通过选择、交叉、变异操作的优化步骤如下:
第1步,输入电力网络信息,包括支路信息和节点信息等。
第2步,建立适应度函数,按照目标函数和约束条件,可建立的适应度函数如式(13)所示:
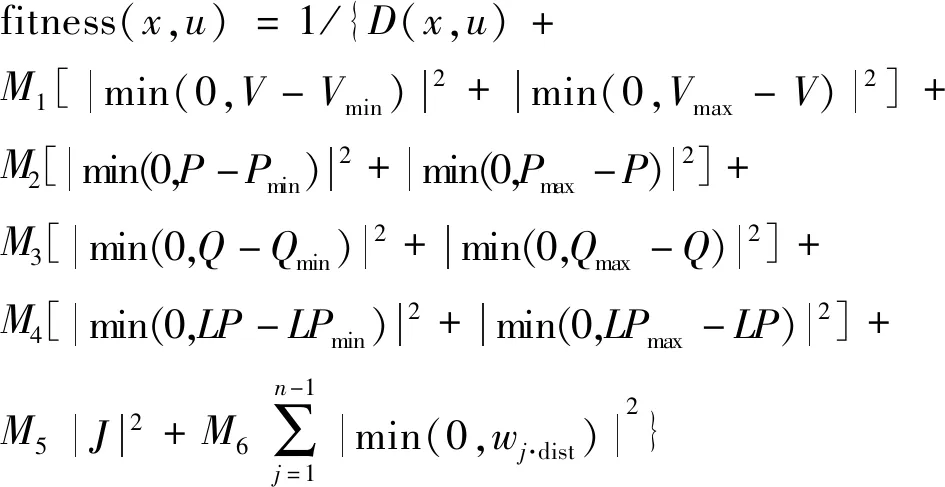
(13)
式(13)所示参数M1~M6为惩罚系数,对应项约束越界时,使得适应度函数值变小,当适应度函数最大时,即可得到对应的危险距离值。
第3步,随机生成初始种群,验证随机得到的节点注入功率在该网络中的收敛性,收敛则保留,不收敛则重新生成直到收敛为止。
第4步,计算每个个体的适应度函数值,验证结果,并输出此时的危险距离和对应的节点注入功率。
其优化流程图如图3所示。

图3 基于基本遗传算法计算危险距离的流程图Fig.3 Flowchart of calculating the danger distance based on the basic genetic algorithm
5 算例分析
为说明针对连锁跳闸的危险度数学模型以及求解算法,以IEEE-39节点系统为算例进行演示。IEEE-39节点系统的接线如图4所示,该系统的元件参数及节点注入功率数据可参见文献[9]。根据该网络发生过载,其距离后备保护的动作特性采用方向圆特性。

图4 IEEE39节点系统接线图Fig.4 IEEE39 node system wiring diagram
(1)计算危险度的基本遗传算法参数设置如表1所示。
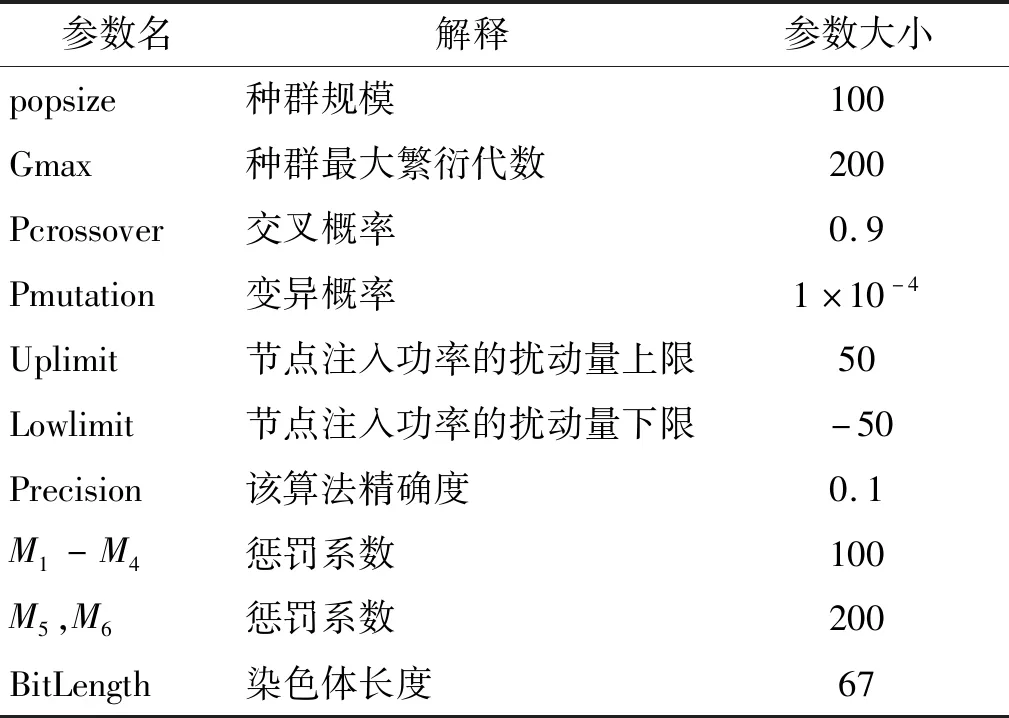
表1 计算危险度的基本遗传算法的参数设置Tab.1 Parameter setting of basic genetic algorithm for calculating danger level
(2)计算危险度的基本遗传算法求解的过程如下:
1)读取网络节点电压、节点注入功率和支路参数等信息,设定基准功率为100 MVA,基准电压为115 kV,以下计算相关数值均采用标幺制。
2)根据1)的信息,检验网络正常运行状况下和初始线路切除后的潮流收敛情况,收敛则继续向下运行,不收敛则对节点注入功率根据限值进行随机改动,验证收敛后继续运行。
3)编码个体,随机生成种群的每一个个体及其位置元素,位置元素值以二进制编码串表示。
在本例中,种群任一个体i的位置可表示为
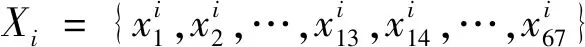
(19)
式中所示,该个体的所有位置元素用矩阵表示,每个矩阵是由二进制组成的随机量,由此形成的初始化的随机种群即为
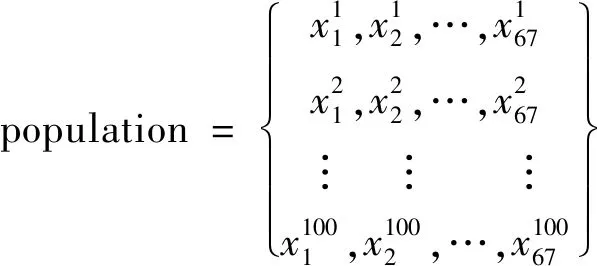
(20)
式(20)的元胞数组显示的行数为种群的个体数,列数为每个个体的位置元素数。
4)计算种群的适应度和累加概率。
5)通过计算危险度的基本遗传算法的选择、交叉和变异将种群进行更新换代,使用轮盘赌法[10]选择进行交叉的个体对。根据交叉概率决定被选择的个体对是否进行交叉操作,再根据变异概率决定被选择的个体是否进行变异操作,形成新一代种群。
6)将新种群进行解码,将用二进制表示的位置坐标转化为十进制表示。
7)验证形成的新种群潮流收敛后,计算新种群的适应度和累加概率,记录最优个体的适应度值、位置及其目标函数值。
8)满足终止条件后退出运行,输出结果,否则返回5)进行下一轮的循环。
以上程序运行过程中,计算并记录的初始故障后系统瞬时状况与当前运行状况的危险距离D和收敛过程,就不同初始故障线路进行比较的运行结果如表2所示:

表2 计算危险度的基本遗传算法的比较结果Tab.2 Comparison results of the basic genetic algorithms for calculating the danger level
从表2所示可以看出,相较编号为24的线路,编号为16的线路为初始故障线路时,发生连锁跳闸的危险度更高。
6 结论
电网的连锁跳闸现象与初始故障发生前电网的运行状态密切相关。当电网运行于临界状态附近时,是相当危险的,一旦发生初始故障,极易引起连锁跳闸。本文结合了连锁跳闸实际行为中继电保护的动作,提出基于危险度分析的方法,给出了较为严密的数学表示形式,可有效评估电网当前的运行状态是否处于临界状态及其与临界状态距离的远近,并通过仿真验证了方法的有效性。该方法可为后续的研究提供一定的借鉴。
