基于BP神经网络的运动文胸肩带属性与乳房振幅的函数关系
2019-10-09马秋瑞
周 捷, 马秋瑞
(西安工程大学 服装与艺术设计学院, 陕西 西安 710048)
近年来,健身美体已经在社会群体中成为一股潮流,由于乳房没有骨骼的支撑,女性在运动过程中往往会感到胸部不适[1],严重可能会对乳房弹性组织造成不可逆转的伤害,危及女性身体健康[2-3]。运动文胸能够较好的支撑乳房防止乳房被拉伸,其肩带对胸部起到提拉和保护的作用,也是运动文胸一个至关重要的组成部分[4-5]。
目前对于肩带的研究主要在造型设计[6-8]、结构设计[9]、材质属性[10-11]和肩带对人体的压力[12-14]等方面。甘应进等[6]主要针对“肩带滑落”这一问题,得出了肩带设计的最优角度;李立新等[8]将肩带工艺设计与文胸时尚设计结合起来,讨论了肩带设计在文胸整体设计空间中所发挥的重要作用;于晓坤等[11]基于力学理论,对肩带拉伸性能与材料属性之间的关系做了相关分析;王丽卓等[14]对肩带压强分布规律做了相关测试,并发现肩带压强规律。这些研究的重点是基于肩带的静态物理性能。
人体在运动时,肩带的不同材质性能对于乳房运动的控制程度存在一定的差异[15-16],其关系受到外在和内在因素的干扰变得非常微妙,传统的方法较难探索出它们之间的关系。
BP神经网络具有强大的非线性逼近功能,在利用该网络做预测研究时,传统做法是用一组肩带属性作为网络输入,乳房振幅作为目标输出,训练出一个对应的网络,然后将另外一组未经训练的肩带属性输入网络中对乳房振幅做出预测。然而,网络内部的计算过程和具体函数关系并不知晓,得到的网络就像一个黑箱模型,只能通过输入来预测输出,并不了解不同属性的肩带对乳房振幅的影响程度和它们之间的关系,更不能根据网络内部具体计算关系对网络做出较好的改进。
本文基于BP神经网络内部计算原理,通过调整网络3个参数,得到肩带的3种属性与乳房振幅对应网络的正向推理关系,最终确定肩带的不同属性对乳房运动影响的权值和阈值,建立肩带属性与乳房振幅之间的关系模型。
1 实验部分
选取8位胸部尺寸在75B到85D之间的女大学生作为本文实验被测人员,从38种宽度为1.6 cm常用的商用肩带中选择9种不同材料属性的肩带作为本文实验的控制变量,肩带如图1所示,这9种肩带涵盖了所有的肩带属性范围值。

图1 肩带Fig.1 Shoulder straps
运动测试前首先在被测人员左乳房的胸高点处贴1个标记点,再以这个标记点为中心,向上贴2个标记点,间距为4 cm,再分别向左、右及下方4 cm处贴上3标记点,用这6个标记点(M1~M6)来记录乳房的运动。另外4个标记点(R1~R4)为参考点,记录人体胸廓的运动[15],这10个标志点如图2所示。静态测试时,被测人员保持静止站立姿势。运动测试时,被测人员在跑步机上以7 km/h的速度做跑步运动,用英国Oxford Metrics Limited公司的VICON光学运动捕捉系统以120 Hz的频率同时记录10个标记点的三维坐标。
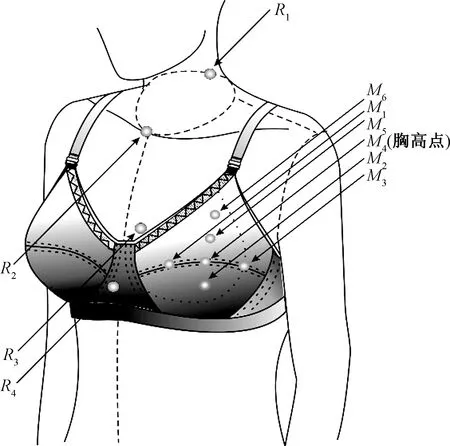
图2 10个标记点Fig.2 10 test markers
此次测试在安静的实验室内完成,测试温度为20 ℃,相对湿度为(65±2)%,风速小于0.1 m/s;测试前,被测人员经过专业人员的相关测试培训,达到要求方可参加测试。测试时,专业人员选择合适尺码的运动文胸,然后通过调节文胸后背扣的位置和肩带的长度,确保罩杯与每位被测人员的胸部贴合。通过随机抽取来更换9种不同肩带进行运动测试。每种肩带进行3次运动测试,其间被测人员休息5 min;更换下一种肩带时,被测人员休息10 min。
2 肩带属性与乳房振幅的关系
2.1 数据处理
首先对收集到的10个标记点的三维坐标数据进行筛选,去除有漏点的数据;在每次运动中选取稳定的20个连续运动周期的三维坐标数据;将原始三维坐标数据进行坐标转换,即,将地面坐标系统转换为乳房坐标系统[16],从而得到乳房相对于人体胸廓的运动数据;分别提取每个运动周期3个方向的最大值和最小值,每个周期同一方向的最大值与最小值的差值,即为该周期下该方向的乳房振幅;求得每个测量点在3个方向的20个运动周期/次×3次运动的180个振幅,然后分别对3个方向振幅求平均,该平均值作为每个测量点在每个方向的振幅,即为1组样本的测量值。
2.2 数据整理
8位被测人员,9种不同肩带,每位被测人员左乳房上有6个标记点,因此,共有432个标记点的样本测量值,如表1所示。每个标记点对应有3个方向(x、y和z方向)的乳房运动平均振幅,用这3个方向的平均振幅作为每个标记点的整体振幅;通过记录乳房上每个标记点在静态时的坐标,可以得到每个标记点与胸部坐标原点的距离(即表1中的距离)。由于每个标记点振幅主要受此距离和文胸肩带的3种属性(即:面密度、伸长率和强力)的影响较大,因此,利用这3种属性作为主要因素,距离作为辅助因素,共4个因素,旨在探索这4个因素与每个标记点整体振幅之间的权值关系。

表1 标记点的样本测量值Tab.1 Sample measurement values for marker points
2.3 BP神经网络算法原理
BP神经网络具有强大的非线性映射功能,尤其在解决具有复杂因果关系的非线性关系时效果突出[17],研究表明一个3层网络结构就可以逼近任意的函数映射关系[18-19],因此,本文将4个因素作为网络输入,每个标记点整体振幅作为目标输出,利用BP神经网络来确定网络输入与目标输出之间的非线性映射关系。BP神经网络算法原理由以下3个步骤组成。
1)训练网络得到最优权值和阈值。构建一个3层的神经网络拓扑结构,包括输入层、隐含层和输出层,如图3所示。

图3 BP神经网络结构拓扑图Fig.3 BP Neural network topology graph
式中:网络输入为p,目标输出t。输入层具有R个神经元,它的权值和阈值分别为w1和b1,p与w1和b1以加权求和的形式传递到隐含层(隐含层有S1个神经元),再通过激励函数f1得到隐含层的输出a1,计算形式见下式。
a1=f1(w1p+b1)
a1继续作为输出层的网络输入,以同样的方法用权值w2和阈值b2,再与a1进行加权求和后传递到输出层(输出层有S2个神经元),输出层通过激励函数f2计算得到输出层的网络输出a2,计算形式见下式。
a2=f2(w2a1+b2)
计算输出层的网络输出a2与目标输出t的均方误差F(x),均方误差计算方法见下式。
F(x)=[t(k)-a(k)]T[t(k)-a(k)]
式中:t(k)表示第k个a2的期望输出值,a(k)表示第k个a2的输出值。网络根据均方误差F(x)进行反向传播,不断调整更新每层的权值和阈值来训练网络,直到网络达到稳定状态,获得1组最优的权值和阈值。
2)仿真预测并检验预测效果。随机抽取1组未经训练的样本,用训练后的网络对此样本的网络输入做仿真预测,最后将仿真预测值与此样本的目标输出值作对比,如果仿真预测值与目标输出值之间的误差小于标准误差,则证明网络性能达到了预测要求[18]。
3)推导函数关系。对经过检验后的网络进行正向知识推理,用每层的传输函数、权值和阈值,推导出网络输入与目标输出的最终关系式。
2.4 BP神经网络计算过程
本文研究所有的操作均在美国MathWorks公司推出的科学计算软件MatLab R2018a环境下完成。
2.4.1 建立网络
分别将表1中的4个因素以432×4的矩阵形式输入到MatLab的工作区中赋值给p,作为网络输入每个标记点整体振幅以432×3的矩阵形式输入在MatLab的工作区中赋值给t,作为目标输出。p与t的每行均一一对应,构成432组样本对。用randperm函数将432组样本对的顺序随机打乱,在打乱顺序后的样本对中,抽取前400组样本对,分别以4×400和400×3的矩阵形式赋值给p1和t1,作为BP神经网络模型的训练组;其余32组样本对分别以4×32和32×3的矩阵形式,赋值给p2和t2作为BP神经网络模型的检验组。
通过p1作为网络输入t1作为目标输出,利用BP神经网络函数newff建立并训练得到一个3层的BP神经网络模型。
2.4.2 调整不同网络参数
由BP神经网络算法原理可知,在使用newff函数建立BP神经网络模型时,为使网络达到最佳状态,需要调整网络中的3个参数,这3个参数分别为传输函数、隐含层神经元个数和训练函数。
1)传输函数。BP神经网络中,输入层到隐含层的传输函数为Sigmoid函数,该函数包含了tansig和logsig 2种函数,tansig函数用f(u)表示,logsig用g(u)表示,计算式分别为:
式中:u为范围是(-∞,+∞)的任意值,logsig函数将u映射到区间(0,1),而tansig函数将u映射到区间(-1,1);由于输出层的输出值为具体的乳房振幅,其值的范围可以达到任意值,因此,隐含层到输出层的传输函数一直使用线性函数(purelin)作为传输函数[21]。
2)隐含层神经元个数。隐含层的神经元个数会对网络性能产生较大的影响,理论上分析,隐含层神经元个数越多,网络性能越好,但是,过多的隐含层神经元个数也会造成网络过拟合现象,而神经元个数不足会使网络容错性差,识别能力低。因此,过多或过少的隐含层神经元个数,都会造成网络最终预测精度不足。到目前为止一直没有找到一个很好的方法来计算隐含层神经元个数,前人根据自己的经验总结出下式来确定隐含层神经元个数的一个大致范围[22]。
式中:n是隐含层神经元个数,ni是输入层神经元个数,no是输出层神经元个数,a是(1,10)范围内的常数。net是以p1和t1作为训练组来建立得到的网络,由于p1和t1分别为4×400和400×3的矩阵,因此,ni是4,no是400,由上式计算得到n的范围为20~29。
3)训练函数。BP神经网络的训练函数代表着网络的训练方式,目前主要有BFGS拟牛顿BP算法函数(trainbfg)、梯度下降BP算法函数(traingd)和梯度下降动量BP算法函数(traingdm)3种训练函数[23]。
为了观察不同参数下的网络拟合效果,分别使用了logsig和tansig 2种传输函数作为输入层到隐含层的传输函数(见表2);隐含层神经元个数设定在20~29之间;分别使用trainbfg、traingd和traingdm作为训练函数,共组合得到60种不同参数下的网络neti,i的范围为1~60。

表2 60种网络net的均方误差Tab.2 Mean square error of 60 kinds of network net
以p1和t1作为训练组,分别输入到60种网络neti中对网络做训练,每种neti在训练完成后,再用p2和t2作为检验组,对neti做检验,也就是,将p2分别输入到60种训练后的网络neti中,每种训练后的网络neti通过p2计算得到T2(即BP神经网络预测出来t2对应的乳房振幅)。
计算每种网络neti的网络输出T2,与目标输出t2(真实的乳房振幅)的均方误差,来比较每种网络neti的预测精确度,计算结果见表2中60种网络neti的均方误差。均方误差计算如下式所示。
式中:m表示均方误差;e为T2与t2中各个元素对应的差值,N为96(32×3,即t2的个数)。
表2中均方误差最小的值为0.023,即认为使用它对应的网络net12时预测性能最佳。net12预测输出的乳房振幅T2和真实乳房振幅t2的均值分别为0.706和0.710,计算它们均值的百分比为99.44%,由此可见,其网络预测值已经达到了真实值的99.44%。由于该网络net12对应的传输函数为tansig、隐含层神经元个数为21个、训练函数为traingdm,因此,这组参数即为BP神经网络预测乳房振幅的3个最佳参数。
2.4.3 确定网络最终关系
为了找到BP神经网络预测乳房振幅的最终关系式,在MatLab中导出net12的权值和阈值,如表3所示。iw1为输入层到隐含层的权值,由于网络的隐含层有21个神经元,输入层p是一个4行的矩阵,因此,权值iw1为一个21×4的矩阵。根据图4中的BP神经网络拟合传输过程可知,iw1与网络输入矩阵p做矩阵乘积运算之后,得到一个21行的矩阵,将该矩阵的每列分别与阈值b1相加,得到一个新的21行矩阵输出,将此输出用tansig函数做函数关系映射,得到输入层到隐含层的网络输出f1(21行的矩阵);iw2(21×3的矩阵形式)为隐含层到输出层的权值,继续将f1作为隐含层到输出层的网络输入,左乘iw2的转置(3行21列矩阵)做矩阵乘积运算后,得到一个3行的矩阵输出,将此输出的每列都与阈值b2相加后,得到隐含层到输出层的网络输出t。此计算过程即为BP神经网络内部计算关系。
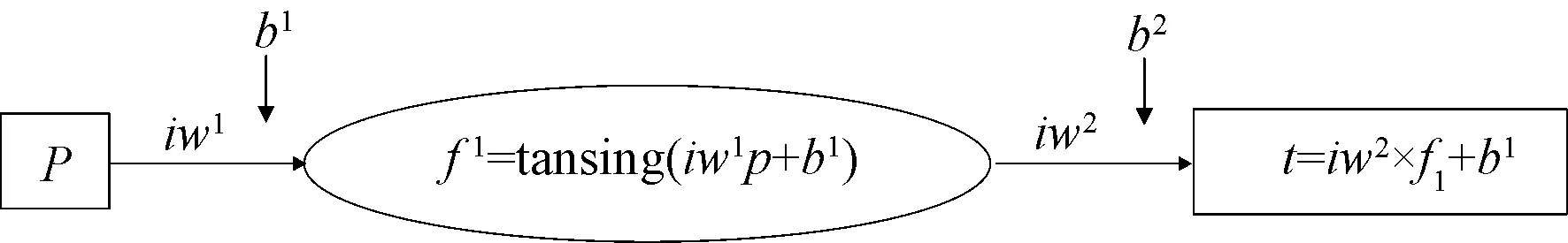
图4 BP神经网络拟合传输图Fig.4 BP neural network fitting transmission diagram
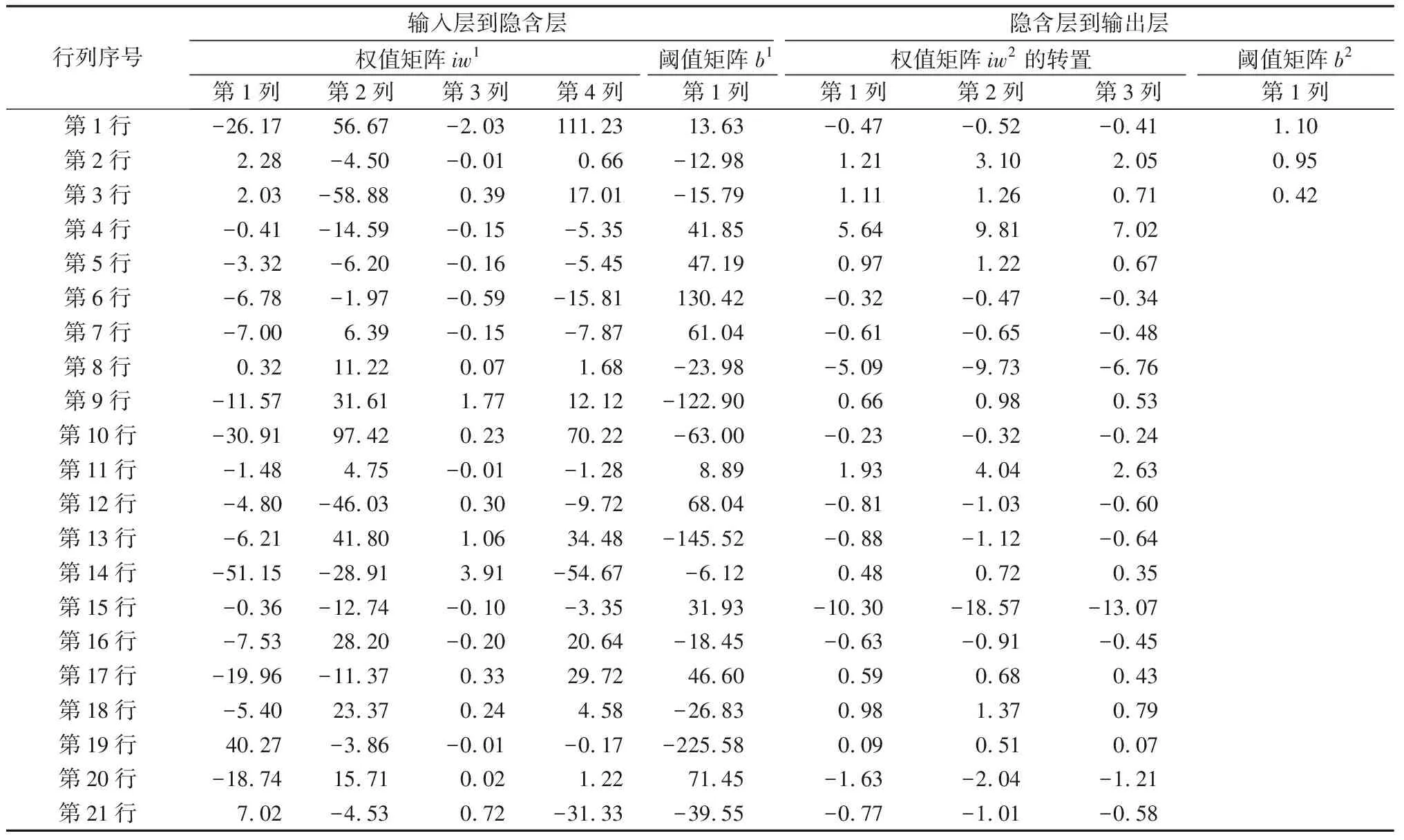
表3 网络最终的权值和阈值Tab.3 Final weights and thresholds of network
根据BP神经网络的拟合传输过程,以及得到的权值和阈值,对p与t的函数关系进行正向推导。基于图4可以得到下式,即为4个因素构成的矩阵p与乳房整体振幅构成矩阵t之间的函数关系模型,基于此模型便可得出3种肩带属性与乳房振幅之间的具体关系。
t=iw2×[tansig(iw1×p+b1)]+b2
3 结 论
本文利用BP神经网络的拟合功能和计算原理,调整BP神经网络3个参数,得出在选取传输函数为tansig、隐含层神经元个数为21个、训练函数为traingdm作为BP神经网络的3个参数时,网络拟合出的乳房振幅达到了真实值的99.44%;最终确定肩带属性与乳房振幅的权值和阈值,以及它们之间的关系模型。
本文研究旨在探索乳房整体振幅与运动文胸肩带3种属性之间的关系,由于目前实验条件有限,本次实验只针对胸部尺寸为75B到85D的女大学生做了相关测试。在后续研究中,将在扩大实验人群的基础上对此项研究展开更加深入的调研。
FZXB
