电脑横机织针的磁驱动设计与建模

张成俊， 游良风， 左小艳， 张 弛， 朱 里

(1. 武汉纺织大学 机械工程与自动化学院， 湖北 武汉 430073; 2. 湖北省数字化纺织装备重点实验室， 湖北 武汉 430073)

电脑横机是重要的纺织生产装备，由其生产的织物应用十分广泛。传统的电脑横机利用往复运动机头内的三角(凸轮)作用于针槽内织针的针踵上，使织针按照编织工艺的要求，完成成圈、集圈、浮线等工艺动作，实现面料上各类花型图案的编织[1]。

注：图上数字为织针号码。图2 织针磁驱动动作示意图Fig.2 Diagram of magnetic driving action for knitting needles. (a) No.1 needle rises to tuck position; (b) No.1 needle rises to stitch transfer position; (c) No.1 needle returns to float position

由于织针的驱动方式为三角与从动件织针间的受力驱动，其本质利用凸轮与针踵间的摩擦驱动织针运动，故在设备运行的过程中，需要保证其良好润滑，避免设备运行中的振动、发热和断针。为减小运行过程的振动和温升，提高设备的运行效率，国内外研究人员从不同的角度对设备进行了优化，Zhao等[2]、Chen等[3]、方圆等[4]等从三角曲线形态和成圈机构的角度对三角的曲线进行了数值计算和优化设计，减小了三角与针踵间的摩擦力；德国格罗茨(Groz-Beckert)公司研制一种名为Litespeed的织针[5]，减轻了织针的质量，减小了织针与针槽间的摩擦力，使运行时温度和能耗均降低了20%；日本福原公司研制了“节能织针”，减小了织针与针槽的接触面积，使运行时温度降低了12%，能耗降低了7%[6]。

上述从三角驱动机构曲线优化和减轻织针质量和接触面积角度的研究，虽然有效地减小了三角与针踵间的摩擦力，但并没有摆脱三角与织针从动件织针受力驱动的机械式驱动原理限制，设备运行时仍存在温升和振动的问题。针对此问题，本文提出织针磁驱动的驱动方法，织针的运动由电磁铁阵列非接触式驱动，彻底改变传统三角与针踵作用的机械式织针驱动方法。本文方法不仅可减小设备运行时的发热和温升，亦可极大地简化横机的结构设计，提高设备的维护性能。

1 横机织针磁驱动结构设计

织针磁驱动的结构示意图如图1所示，采用驱动与执行部件分离的设计方法。由铁芯和线圈组成电驱动电磁铁，电磁铁阵列嵌入在横机的机头结构中，运动电动机带动机头可在水平方向往复移动。织针与永磁体一起形成永磁织针，永磁织针均匀地安装在针板针槽内，形成永磁织针阵列。永磁织针阵列底部安装有隔板，隔板可限制永磁织针阵列在最低位置的位移量。利用电磁控制系统，在机头往复运动的过程中，控制每个电磁线圈流过的电流大小和方向，使电磁铁阵列形成合成磁场，非接触电磁力作用于永磁织针上，使每枚织针可按照其工艺动作，实现升程和回程运动，其动作过程示意图如图2所示。织针1可在电磁铁阵列右侧的合成磁场的斥力作用下，从浮线高度逐步升程至移圈工艺高度，而后在电磁铁阵列合成磁场的合成磁场吸力作用下，从最高位的移圈高度逐步回落至浮线工艺高度。

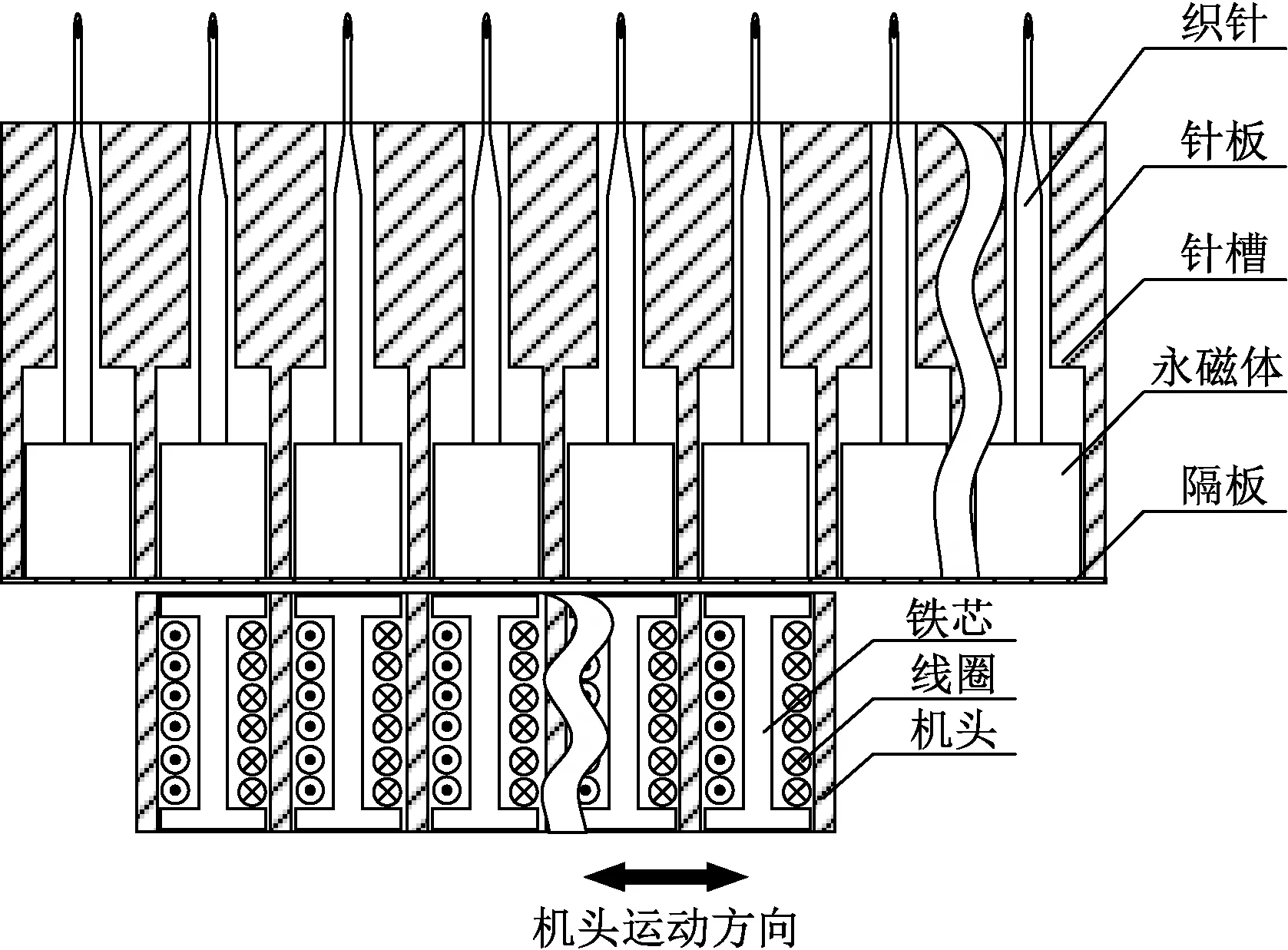
图1 织针磁驱动结构示意图Fig.1 Diagram of magnetic driving structure for knitting needles

2 织针磁驱动等效磁路数学模型

等效磁路法(MEC)常用于磁悬浮轴承[7-8]和电动机[9-10]动态过程分析的一种方法。其利用电阻代替表示气隙处的磁导以及铁芯的磁阻，用电场表示电磁线圈产生的磁场和永磁体产生的磁场。由于电磁铁铁芯由高导磁材料制成，具有磁饱和及磁滞现象，对其进行精确的分析非常困难，为便于分析，本文提出3种假设：1)忽略电磁铁铁芯和永磁体磁饱和、漏磁和涡流；2)不计线圈的反应影响；3)不计温度对磁铁材料的影响。

由于电磁铁阵列与永磁织针阵列采用了非接触式结构方式，在电磁铁阵列与永磁织针阵列的气隙处便有2种磁势源，一种为永磁织针阵列产生的恒定的磁势，另一种为织针驱动电磁铁阵列通入控制电流后产生的励磁磁势。在编织运动时，通过控制电磁铁线圈流入电源的大小和方向，使气隙中的合成磁势发生变化。当电磁体线圈中通入电流的方向，使电磁铁铁芯的磁极与永磁极性相同，其气隙磁密增强，起增磁作用；反之，通入电流的方向使铁芯磁极与永磁极性相反，其气隙磁密减弱，起弱磁作用[11]。

织针磁驱动结构尺寸参数如图3所示，由于安装尺寸及各部分的间隙较小，尺寸忽略电磁线圈与机头安装座之间的间隙。

注：1，2，3分别是不同位置的永磁织针；4，5分别是不同位置的电磁铁铁芯。图3 织针磁驱动结构尺寸Fig.3 Dimension of magnetic driving structure for knitting needles

永磁织针永磁体部分的极化方向高度hm，电磁铁铁芯宽度为Lm，2个电磁铁间的间隔尺寸为Lb；永磁体底部与电磁铁铁芯顶部间隔为g；永磁织针与隔板侧壁间隙为δ；永磁织针1与电磁铁铁芯4之间的移动距离为x。

设单个电磁线圈的磁通量为ΦL_q,q=1,2,…；单个永磁织针的磁通量为Φn_q,q=1,2,…；永磁织针与织针隔板的侧壁间隙磁阻为Rs；2枚永磁织针间的磁阻为Rmm；永磁织针1与电磁铁铁芯4相对部分的磁阻为Rm1；永磁织针2与电磁铁铁芯4相对部分的磁阻为Rm2；永磁织针1与电磁铁铁芯4形成气隙的磁阻为Rg1；永磁织针2与电磁铁铁芯4形成气隙的磁阻为Rg2；单个线圈绕组的磁动势为FL；单个永磁织针的磁动势为Fm；横机机头中电磁铁的个数为n，电磁线圈的匝数为N，流过电磁线圈的电流为iq,q=1,2,…，A。

采用电磁铁与永磁织针间的位置关系，建立其有限元模型，如图4所示。

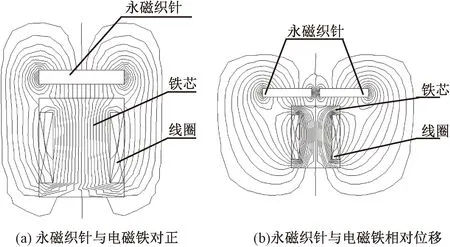
图4 磁路分析模型Fig.4 Magnetic circuit analysis model. (a) Alignment of permanent magnet knitting needles with electromagnet; (b) Relative displacement between permanent magnet knitting needlesand electromagnet

2.1 电磁铁小位移时的磁路模型

如图3所示，当永磁织针与电磁驱动铁芯移动距离小于永磁体的间隔距离Lb时，永磁织针1与电磁铁铁芯4形成相对关系，根据图4(a)所示的磁路模型，其等效磁路模型如图5所示。

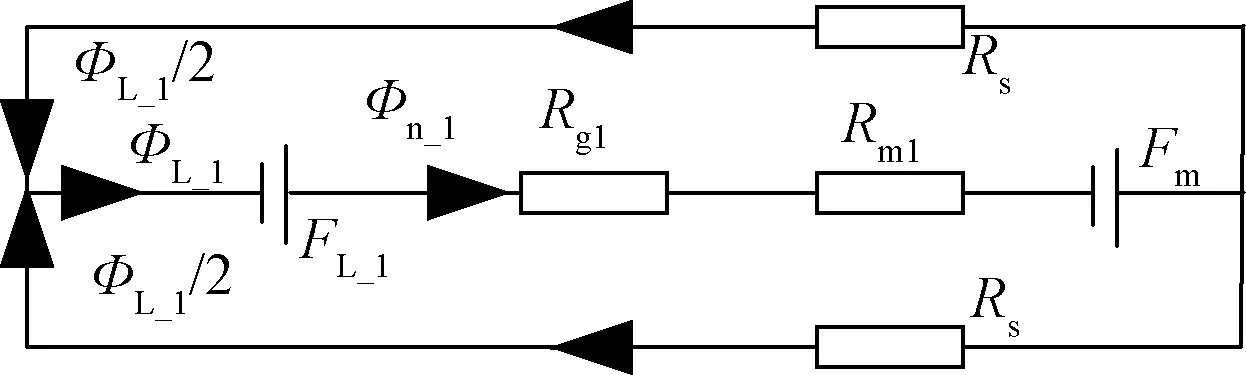
图5 小位移等效磁路模型Fig.5 Small displacement magnetic equivalent circuit model

(1)

Rg2=0

(2)

(3)

Rm2=0

(4)

(5)

FL_q=Ni1

(6)

Fm=Hchm

(7)

Fm+FL_1=ΦL_1(Rg1+Rm1+Rs/2)

(8)

Φn_1=ΦL_1

(9)

求解方程(1)～(9)，可得

(10)

式中：μ0为空气磁导率，H/m；μr为永磁体相对磁导率，H/m；a为永磁体厚度，m；永磁织针与隔板侧壁间隙为δ，m；x为永磁织针底面与电磁铁铁芯位移距离，m；N为电磁线圈的匝数；i1为流过电磁线圈的电流，A；hm为永磁体的高度，m；Hc为永磁体材料的矫顽力，A/m。

2.2 电磁铁大位移时的磁路模型

如图3所示，当永磁织针与电磁驱动铁芯移动距离大于永磁体的间隔距离Lb时，此时永磁织针1和2作用于同一个电磁铁铁芯4上，根据图4(b)所示的磁路分析模型，其等效磁路模型如图6所示。

图6 大位移等效磁路模型Fig.6 Large displacement magnetic equivalent circuit model

(11)

(12)

(13)

(14)

(15)

2Fm+FL_1=Φn_1(Rg1+Rm1)+(Φn_1-Φx)Rs+

Φn_2(Rg2+Rm2)+(Φn_2+Φx)Rs

(16)

(17)

(18)

式中：Lb为永磁织针间的间隔尺寸，m。

联立方程(6)～(7)、(11)～(18)，可得

(19)

2.3 永磁织针磁力计算模型

磁场力的基本计算公式：

(20)

式中：F为磁场力，N；Φ永磁织针的磁通量，Wb；S为永磁织针与电磁体的正对面积，m2。

当电磁铁的移动距离x≤Lb时，

(21)

当电磁铁的移动距离x>Lb时，

(22)

假设永磁织针的质量为m，kg；横机针板与水平面的夹角为θ，(°)；永磁织针受力示意图如图7所示。

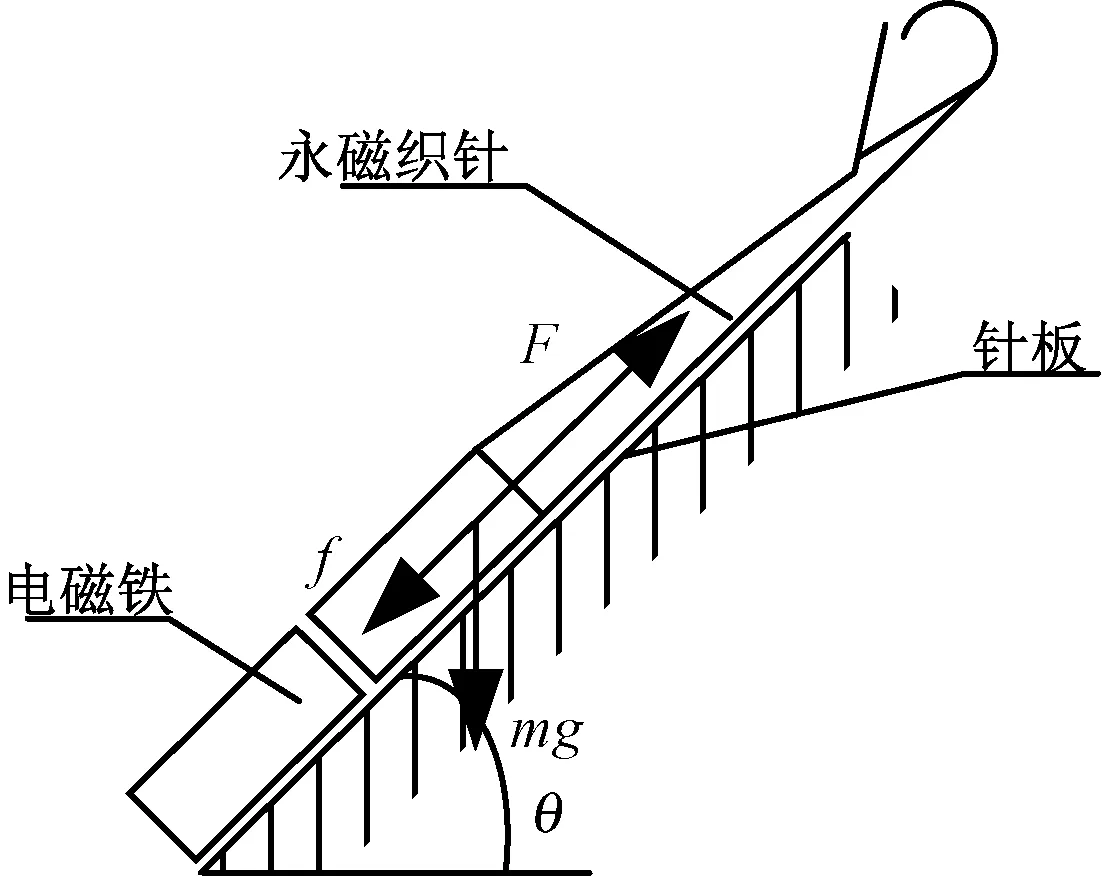
图7 永磁织针受力示意图Fig.7 Force diagram of permanent magnet knitting needle

永磁织针的受力方程：

Fneedle=F-f-mgsinθ

(23)

式中：Fneedle织针受力，N；F为织针所受的电磁力，N；f为织针所受的摩擦力，N。

3 Maxwell仿真分析

电磁阵列驱动结构尺寸参数如图8所示，利用Maxwell 3D建立电磁阵列的驱动模型如图9所示。

图8 磁力模型的尺寸参数Fig.8 Dimension parameter of magnetic driving model

图9 Maxwell 3D磁阵列模型Fig.9 Maxwell 3D magnetic array model

磁阵列结构的材料设置如下：永磁体材料为NdFe35，永磁极化方向为Z轴正向；电磁线圈材料为铜，匝数为1 000，电流大小为1 A；铁芯材料为钢。

在忽略永磁织针重力的情况下，通过改变磁阵列结构永磁织针与下方电磁铁铁芯的对正关系x，当x=0时刻，永磁体与下方的电磁铁铁芯完全对正。随着电磁体向左侧移动的距离x增大，则永磁体将逐步与2个电磁铁形成对正关系，随着移动距离x的进一步加大，永磁体会与下一个电磁铁铁芯完全对正。图9中从左至右第2个永磁体的Maxwell仿真受力数值与本文等效磁路模型计算的曲线对比如图10所示，其中横坐标x为电磁阵列的位移量，纵坐标为永磁织针所受的电磁力数值。

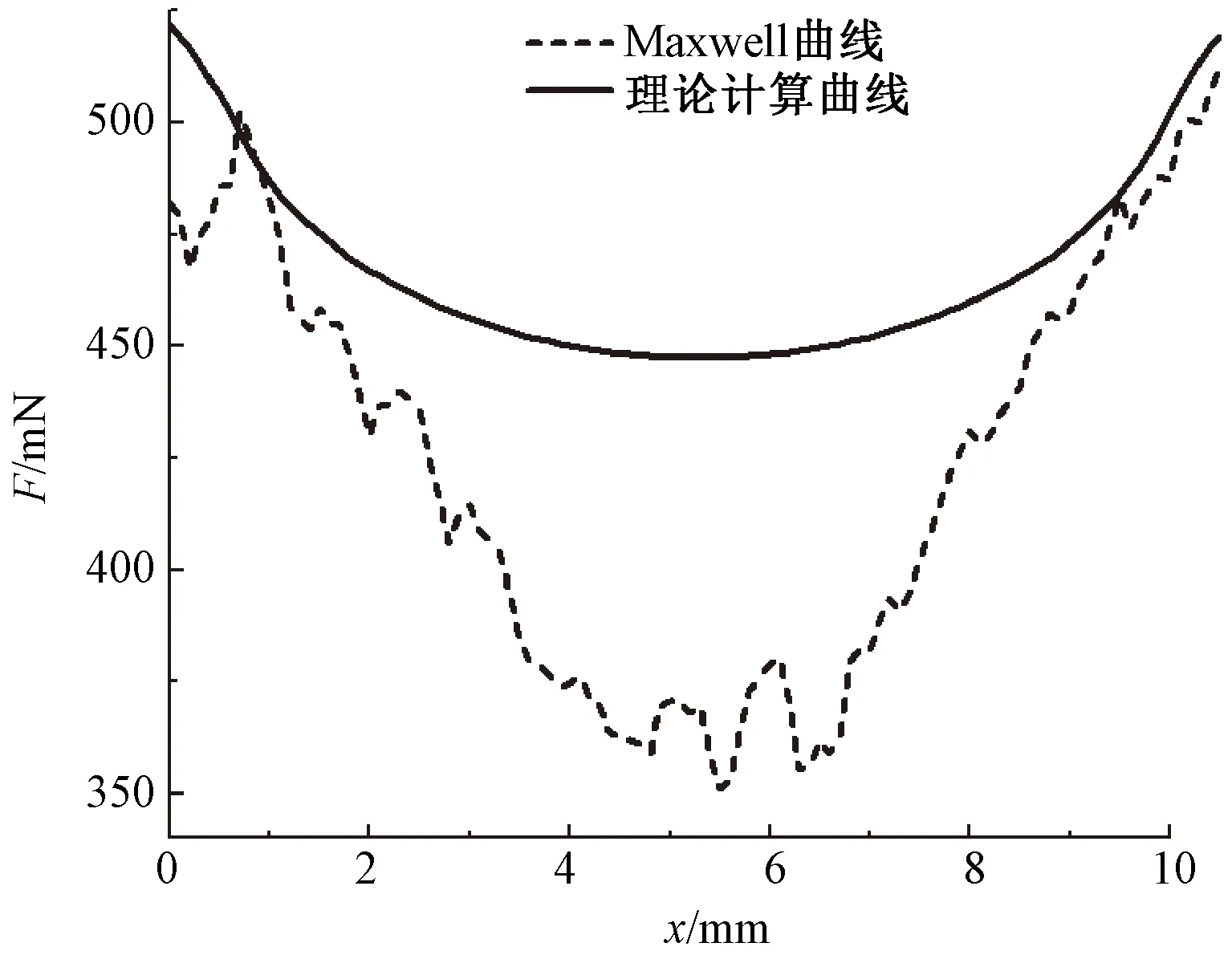
图10 磁路模型数据与Maxwell仿真数据对比Fig.10 Data comparison between magnetic circuit model data and Maxwell simulation

通过图10等效磁路模型计算的结果与利用Maxwell软件运动仿真的结果对比，可以看出，二者在永磁织针受力的变化趋势上具有一定的相似性。但等效磁路模型计算的织针受力较Maxwell仿真的数值大，其主要原因是在等效磁路模型建模过程中忽略电磁铁铁芯和永磁体磁饱和、漏磁和涡流，当永磁体与电磁铁铁芯完全对正时，电磁铁铁芯的漏磁小，故该理论模型与仿真模型数据几乎一致，而在1个永磁体对应2个电磁铁铁芯的时刻，其铁芯的漏磁最大，其理论计算的数值与仿真的数据的差值亦最大。由此可见，本文针对磁阵列的等效磁路分析具有可行性，为进一步分析永磁织针的实际受力奠定基础。

4 结束语

本文在分析传统针织横机织针驱动方法的基础上，提出一种驱动部件与执行部件分离的非接触式织针磁驱动方法。通过控制移动机头内的电磁铁的驱动电流大小和方向，改变电磁铁与永磁织针间的驱动磁力，实现针织横机永磁织针的高度控制。为了实现针织横机织针的磁力驱动，本文采用等效磁路方法，将电磁铁阵列和永磁织针等效为磁势源，将气隙处的磁导和铁芯等效为电阻，利用数学推导的方法，分析了永磁织针在电磁阵列的磁力作用下，机头位移过程的磁力驱动模型，并计算出机头移动1个针距过程的磁通，并由此磁通进一步推算出机头移动过程的驱动磁力表达式。最后，利用经典的电磁仿真软件建立了电磁阵列结构的软件模型，并对比了等效磁路模型和软件仿真模型在单个永磁织针与下方电磁铁铁芯对正关系发生变化时的受力数值，通过数值的对比，验证了磁路分析模型在忽略电磁铁铁芯和永磁体磁饱和、漏磁和涡流等情况下的正确性。

本文提出的针织横机织针的磁驱动结构具有无摩擦、噪声小的特点。针对阵列式织针磁驱动等效磁路模型的研究结论，可为织针的磁驱动设计提供关键的数据参考，也为我国新型针织横机设计提供一种可行的技术方案。

FZXB