基于OWGA算子的辅导员业绩评价研究

李芹影，郑玛丽

《中共中央国务院关于全面深化新时代教师队伍建设改革的意见》明确指出，要重视各级各类学校辅导员专业发展。辅导员是高校与学生打交道的直接教育工作者，是“培养什么人、怎样培养人、为谁培养人”理念的直接贯彻者。因此，如何对辅导员业绩进行科学、客观、全面、公平的考核是一个值得研究的重要问题。

一般来说，辅导员的综合评价包括指标体系和评价方法两个基本要素，其完成过程分为数据的收集和处理、确定指标权重与综合分析3个阶段。采用简单的排序方法经常会使结果与实际情况出入较大，只有运用科学的排序方法才能更好地反映辅导员的工作业绩，对辅导员进行两两比较并给出评价信息更符合实际情况。在确定权重方面，赋予客观公正的评委较大的权重，打分区分度不大的评委较小的权重。基于这些考虑，引入多属性决策方法，建立基于OWGA算子的辅导员业绩评价模型。

一、OWGA算子

有序加权几何平均（OWGA）算子是一种能够有效集结数据信息的方法[1]。其定义如下：设 GW：Rn→R为 n 元函数，W=（w1，w2，…，wn）T是与函数 GW相关的加权向量，满足，若，其中 bi是 a1，a2，…，an中按照从大到小的顺序排列的第i个大的元素，则称函数GW是n维有序加权几何平均算子，记为OWGAW算子，简记为OWGA算子。

说明：（1）OWGA 算子将数据 a1，a2，…，an按照从大到小的顺序重新排列，并通过加权集结，而且元素ai与bi没有关系，wi只与集结过程中的第i个位置有关。

（2）在多人决策模型中，需要每个专家对决策方案进行两两比较，给出互反判断矩阵的偏好信息，为了结合每个专家给出的有效信息，我们可以使用OWGA算子对互反判断矩阵进行集结处理。集结而成的互反判断矩阵在一定条件下仍保持互反性，从而确保了利用组合判断矩阵进行方案排序的准确性。

二、辅导员业绩评价模型

假设对某二级学院的m个辅导员进行评价。首先，通过班级投票或推荐的方式产生n1个学生评委，这些评委是班级的骨干，对辅导员的工作比较了解，办事公平公正，能反映学生的心声；然后，从学生处领导、二级学院党总支书记及院长中选出n2个评委，这些评委对辅导员贯彻党的教育方针以及学校、二级学院各类工作的情况比较了解。评委共有n个，n=n1+n2。m个辅导员相当于m个决策方案，n个评委相当于n个专家决策者。评委对辅导员的评价很难用“好”或“差”进行笼统的评价，“好”与“差”之间还有等次，比如“好很多”“好一点”“好一点点”等，这都是比较出来的结论，而对辅导员进行两两比较给出评价信息更符合实际情况。因此，可以把辅导员之间优劣比较的评价细分为17个，n个评委对m个辅导员给出的两两比较的语言短语集合为：

其中，大于1的数，数值越大说明甲比乙好的程度越大；“1”说明甲与乙两个人水平相当；小于1的数，分母越大说明甲比乙差的程度越大。

每位评委根据某种评价准则从语言短语集合中选择1个数据给辅导员两两比较进行打分，得到n个m×m阶的语言判断矩阵，每个矩阵都是互反判断矩阵。为了反映n个评委的偏好，对得到的判断矩阵的偏好信息进行集结处理，利用OWGA算子进行集结，同时采用模糊语义量化算子（BUM函数）的方法确定其权重。

令 A={a1，a2，…，am}为所有辅导员构成的集合，其中 ai表示第 i个辅导员，i=1，2，…，m。D={d1，d2，…，dn}为所有评委构成的集合，其中dl表示第l个评委，l=1，2，…，n。在某一准则下，评委dl对A中辅导员进行两两比较，得到互反判断矩阵，其中表示评委dl认为辅导员ai对比辅导员aj的优秀程度，满足。

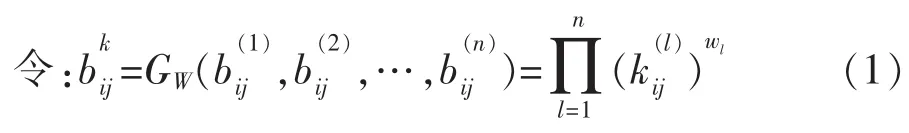
权重向量 W=（w1，w2，…，wn）T由模糊语义量化算子Q确定，即：

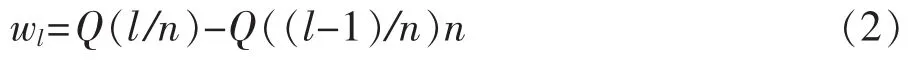
Q（y）由如下的分段函数来确定：

式中，参数 a，b，y∈[0，1]，对应于模糊语义量化标准的“尽可能多”“至少半数”“大多数”的算子Q的参数（a，b）分别为（0.5，1）、（0，0.5）、（0.3，0.8）。则称是 n 个互反判断矩阵 B（1），B（2），…，B（n）利用OWGA算子进行集结所得到的组合判断矩阵。如果a+b=1，则保持互反性，该矩阵反映了 n个评委对m个辅导员进行两两比较得到的综合评价信息，这一矩阵排序反映了评委的共同偏好。

下面给出一个具体实例来说明上述模型。

假设某二级学院共有甲、乙、丙、丁4个辅导员，其语言短语集合为：

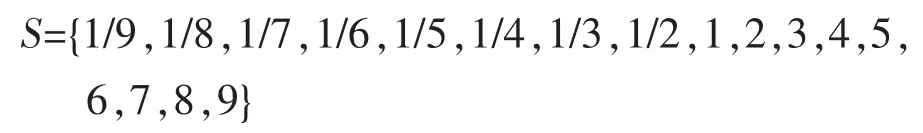
现有学生代表、学生处领导、二级学院领导共5个评委 f1、f2、f3、f4、 f5分别对甲、乙、丙、丁 4 个辅导员给出两两比较的偏好信息，并从S中选出一个数据信息进行评价，得到5个互反判断矩阵如下：

对应模糊语义量化标准的“大多数”的算子Q的参数（a，b）为（0.3，0.7），可知 a+b=1，能够保证由 OWGA算子得到的组合判断仍然保持互反性。利用式（2）与式（3），可以得到OWGA算子的权重系数：

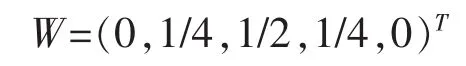
权重系数越大说明该评委给出的评价对排序结果的影响越大；权重系数越小说明该评委给出的评价对排序结果的影响越小；权重系数为0说明该评委给每个辅导员的打分差不多，分不出层次，对排序不起作用。如评委f3的权重为1/2，作用最大；评委f2与评委f4的权重都为1/4，作用其次；评委f1与评委f5的权重都为0，作用不大。

按式（1）利用Mathematica软件计算OWGA算子可得判断矩阵为：

这一结果表明：（1）辅导员甲比辅导员乙差，但比辅导员丙、辅导员丁好；（2）辅导员乙比辅导员甲、辅导员丙好，但比辅导员丁差；（3）辅导员丙比辅导员甲、辅导员乙差，但比辅导员丁好；（4）辅导员丁比辅导员甲、辅导员丙差，但比辅导员乙好。

综合这一结果得出如下结论：辅导员丁最优，辅导员乙次之，辅导员甲再次之，辅导员丙最差。

三、结语

首先，从学生代表、学生处与二级学院领导中选出有代表性的评委，这些评委对每一位辅导员进行两两比较，在给定的语言评价短语集合中选择一个分值进行打分，得到偏好矩阵。其次，利用模糊语义量化算子使得客观公正的评委获得更大的权重，而对打分区分度不大的评委赋予较小的权重。最后，利用OWGA算子建立辅导员业绩绩效评价模型，并给出实例说明此方法的有效性。