2019年高考北京卷第21(5)题的深入探讨

戴耀东

(海门市证大中学，江苏 海门 226100)

1 原题再现

牛顿设想,把物体从高山上水平抛出,速度一次比一次大,落地点就一次比一次远,如果速度足够大,物体就不再落回地面,它将绕地球运动,成为人造地球卫星．

同样是受地球引力,随着抛出速度增大,物体会从做平抛运动逐渐变为做圆周运动,请分析原因．

参考答案:物体初速度较小时,运动范围很小,引力可以看作恒力——重力,做平抛运动;随着物体初速度增大,运动范围变大,引力不能再看作恒力;当物体初速度达到第一宇宙速度时,做圆周运动而成为地球卫星．

2 答案分析与思考

参考答案充分考虑学生的认知水平,根据速度不同导致的运动范围变化,从而考虑力方向是否能看成恒力．此模型来源于人教版必修2第44页,却巧妙考察学生平抛运动和圆周运动的条件,从一般到特殊的物理思维,还有巧取近似的物理方法,是一道很好的高考题．

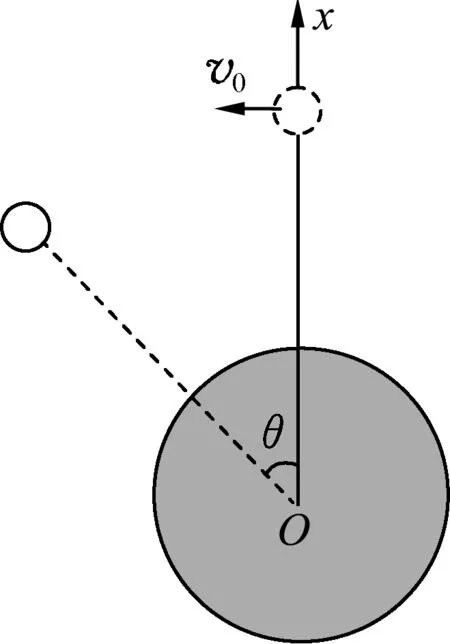
图1

这里存在一个值得思考的问题,这个平抛运动是怎么因为速度变大,就逐渐过渡到圆周运动的呢?抛物线能因为速度增大变成圆吗?笔者尝试利用大学的分析力学和解微分方程的知识回答这个问题．

3 解决问题

3.1 建立模型

如图1,以地球球心为极点,Ox轴为极轴建立极坐标系,θ为极角(逆时针方向为正)．

在极坐标系中，er为单位位矢,eθ为单位角矢，

由于引力F始终沿-er方向,所以

2vrω+rβ=0.

根据牛顿第二定律可得

又根据开普勒第二定律可知

r0v0=r(rω),

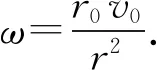
于是

(1)

3.2 求解微分方程

此微分方程的求解主要用到换元技巧,具体如下.

代入(1)式可知

(2)

两边积分,并代入初始条件(r=r0时v=v0),可得

即

(3)

又因为

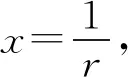
以上两式先后代入(3)式可得

(4)

即

即物体在一般情况下的轨迹方程为

(5)

3.3 结果分析

(1) 若v0较小,e→-1.

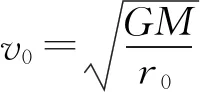
物体的轨迹方程为r=r0,这恰好是圆的极坐标方程．

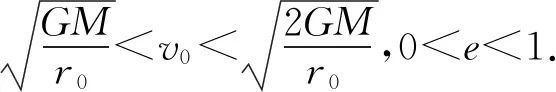
物体的轨迹方程椭圆的极坐标方程．

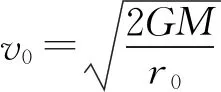
物体的轨迹方程双曲线的极坐标方程,即若物体初速度超过第二宇宙速度,物体将沿着双曲线远离地球．

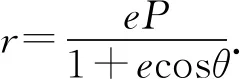
4 总结

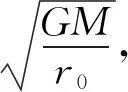
本文对2019年高考北京卷第21(5)题作了定量分析，便于更好理解本题的本质.