高中物理力学解题中整体法的运用
2019-10-09■王刚
■王 刚
整体法在力学解题中应用很广,下面举例说明。
一、整体法解题思路分析
整体法是将多个物体看成一个整体,并对其进行受力情况分析,有效简化复杂的物理题型的解题方法。在应用整体法的过程中,需突破常规的思维限制,对需探讨的对象进行隔离,使其成为一个“单独的”总体。
二、运用分析
1.基于运动过程的应用方法:使用整体法能够系统分析物体在不同阶段的运动情况,简化受力情况。
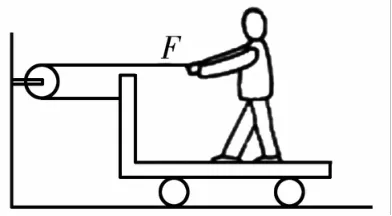
图1
例1如图1所示,人的质量为m、小车的质量为M,人用水平力F拉绳子,图中两段绳子均沿水平方向,不计滑轮质量及摩擦,若人和车保持相对静止的状态,且水平地面是光滑的,则车的加速度为多少?
分析:该题需求车的加速度,似乎需将车隔离出来才能实现求解,实则不然。采用整体法(将小车与人看成一个整体),结合牛顿第二定律的定义,方可求解出结果。
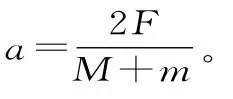
例2一个质量为1kg的小球从h=20m的高处自由下落到软垫之上,反弹后上升的最大高度5m,小球与软垫的接触时间为1s,在接触时间内小球受合力的冲量大小为多少?(空气阻力忽略不计,取g=10m/s2)
分析:小球从最高点释放后,会经过下落阶段、与软垫的接触阶段,以及反弹上升阶段。历经这一系列流程后达到最高点。在此过程中,动量没有发生变化,初动量、末动量的数值都为0。使用整体法将这三个过程视为一个过程,可简化处理该题,如图2。

图2

2.基于物体相互作用的应用方法:物体相互作用方面的问题主要发生在含有动摩擦力、静摩擦力的问题情境中。因此,运用整体法,结合牛顿第二定律、机械能守恒定律、动量守恒定律可完成求解。
例3两刚性球a和b的质量分别为ma和mb,且这两个球的直径分别为da和db(da>db),将a、b两球依次放入一竖直放置、内径为d(da<d<da+db)的瓶底圆筒内,如图3。假设a、b两球静止时对圆筒侧面的压力大小分别为f1和f2,筒底所受的压力大小为F。已知重力加速度大小为g,且所有接触面都是光滑的。那么压力F与两刚性球的质量有什么关系?
分析:将a、b两球看成一个整体,并对整体进行受力分析,能够得到其关系。
解:将a、b两球视为一个整体,在竖直方向上仅受到重力,整体对侧壁产生的压力沿水平方向,因此压力不能增大对底部的挤压,即F=(ma+mb)g。在水平方向上,整体受力平衡,即f1=f2。
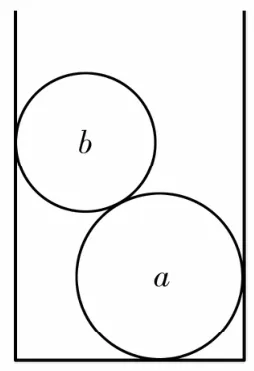
图3
