高中数学中的“齐天大圣”

■吴吉云

“齐次式”在高中数学中出现的频率比较高。对“齐次式”的处理关键是化二元为一元,即化繁为简,化陌生为熟悉。下面我们从多种题型中玩转“齐次式”,去感受多题一解的奇妙。

1.齐次式在三角函数中的应用

1.1 齐次式在三角函数化简求值中的应用

小结：当所求式子为关于sinα与cosα的“齐”次分式时,分子分母同时除以cosα或cos2α可以转化为关于tanα的式子。

1.2 齐次式在正弦定理中的应用

例2设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为____。

小结：当式子是关于边a,b,c或关于sinA,sinB,sinC的“齐次式”时,可用正弦定理进行化简。

2.齐次式在解析几何中的应用

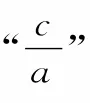
3.齐次式在不等式中的应用

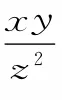
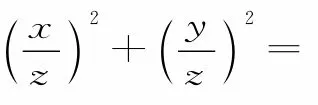
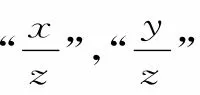
结束语：齐次式在高中数学解题过程中是比较活跃的,在解决相关知识的齐次式时,如果我们能灵活准确地观察出式子的特征,用减元思想进行化简,就可以大大提高我们的解题速度和准确度。