高中数学数列部分的学习及解题策略

■朱业辉

同学们在学习数学知识的过程中应当重视基础知识的学习,不断研究高效解题策略。下面以数列知识为例,介绍一些学习策略和解题策略。

一、高中数学数列部分学习策略

数列相关知识作为高考当中的重难点内容,蕴含着十分丰富的数学解题方法和数学思维框架内容,学好数列知识,能够帮助同学们在学习其他数学知识的时候保持清晰的思路,提升学习效果。

比如,我们在学习等差数列这部分知识的时候,就可以在了解等差数列概念和基本求解方法以后,找寻将数列知识与情境联系在一起的学习方法。如,作为世界七大奇迹之一的泰姬陵中就有一个十分奇妙的三角形图案,这个图案建筑是通过相同的宝石而镶嵌成的,并且整体高度能达到一百层楼之高。我们可以进行思维拓展,想一想是否能够利用等差数列的求和公式来计算泰姬陵的这个三角形图案究竟使用了多少块宝石进行镶嵌。在这样的情境构建当中,我们不仅对等差数列知识有了更进一步的理解,而且见识、阅历也极大地得到拓展。

二、高中数学数列部分解题策略

1.数列求和解题策略

数列求和是我们在学习数列这一单元知识时的重难点内容,大部分的考试题目都会从数列求和入手进行设计,无法求得数列之和,自然无法进行解题。所以,我们要熟悉并掌握数列求和的解题策略,将常见数列求和方法和解题思路牢记在脑海中,针对不同的数列采取不同的求和方法。一般来说,常见的数列求和方法有:公式法、分组转换法、裂项相消法、错位相减法等。

例1已知{an}是公差不为零的等差数列,数列首项为1,且a1,a3,a9构成等比数列。试求数列{2an}的前n项和。

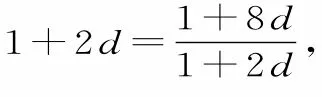
2.通项式求解策略

只有掌握好函数通项式,我们才能够在学习数列知识的时候更加准确地探索出正确解题方法。一般来说,我们常用的函数通项式求解方法有直接观察法、待定系数法、错位相减法等。

例2已知一个数列的前十项为1,1,2,3,5,8,X,21,34,55。请根据给出的数列项求解X的值。

分析：这道题目其实是很基础的一道数列通项求解题目,我们在学习了数列通项式求解相关策略后,还是应当利用比较基础的题目进行练习与巩固。一般来说,如果数列通项求解类题目给出了多个数值来让我们求解数列通项,都是能够先用观察法进行观察,再找寻规律的。通过对数列前十项的观察,我们可以发现第三项其实是第二项和第一项相加的数值,而第四项则是数列第二项与第三项相加而来的,以此类推,就很容易得到数列通项应为an=an-1+an-2(n≥3)。X=13。

总而言之,在高中数学的学习过程中,我们要不断提升自我学习素养,养成良好的学习习惯,并在平时的生活与学习当中不断钻研解题技巧,试着从多个角度找寻最佳方案,提升解题效率。