薄壁圆筒强度计算的相对误差分析

2019-10-08林鸿志杜长城

长春大学学报 2019年8期

黄云，林鸿志，杜长城

(1.西南石油大学机电工程学院，成都 610500，2.西南交通大学力学与工程学院，成都 610031)

图1 薄壁圆筒受扭示意图

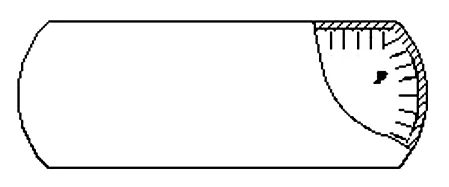
图2 薄壁圆筒受内压示意图

在求解薄壁圆筒扭转和受内压的强度时，如果直径选择不恰当，其相对误差将大于工程中所允许的5%。在有些材料力学教材中，其近似计算公式中直径的选择也没有给出合理的解释，因此,很有必要讨论材料力学中薄壁圆筒受扭和受内压作用时其强度公式中取不同直径的相对误差，以便确定近似公式中应选何种直径。在材料力学中，薄壁圆筒的定义与薄壁圆筒的变形形式有关[1-3]，(1)薄壁圆筒受扭时：t/D1/20的圆筒才为薄壁圆筒，其中t为薄壁圆筒的壁厚；D为薄壁圆筒的平均直径Dm，如图1所示。(2)薄壁圆筒受内压时：D为薄壁圆筒的内径Di。在压力容器中[4-5]，Do/Di1.2称为薄容器，如图2所示。

1 薄壁圆筒的强度计算及相对误差分析

1.1 薄壁圆筒受扭时其强度计算和相对误差分析

1.1.1 薄壁圆筒受扭时应力分析

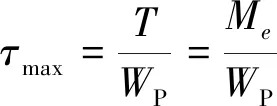
在材料力学中假设薄壁圆筒横截面上的切应力均匀分布，其切应力τ可近似表示为[6]：

1.1.2 薄壁圆筒受扭时应力相对误差分析

如取λ为壁厚与平均直径之比(λ=t/Dm)，式(3)可表示为：

(式4)。

由式(4)可知，当0<λ1/20时，δ1为增函数，可以得出，在薄壁圆筒受扭时，壁厚与平均直径之比越小，采用(2)式计算其切应力与最大切应力的相对误差越小。即满足薄壁圆筒的条件下，相对于平均直径，壁越薄，采用(2)式计算其应力相对误差越小。

现讨论用式(2)来近似计算τmax，如式(2)中D取不同的直径，其相对误差的最大值(即D/t=20时)如表1所示。

表1 薄壁圆筒受扭D取不同的直径最大的切应力的相对误差

由表1可知，薄壁圆筒受扭时，采用式(2)来近似计算其最大切应力，如式中D取平均直径Dm，此时的相对误差小于5%。如取内径Di，其相对误差已大于5%，如取外径Do时，其相对误差高达14.025%，所以，式中的D取薄壁圆筒的平均直径Dm才相对合理。

图3 薄壁圆筒受内压示意图

1.2 薄壁圆筒受内压时其强度计算和相对误差分析

1.2.1 薄壁圆筒受内压时的应力分析

(1)轴向应力

如图3(a)所示的薄壁压力容器厚度为t，内径为Di，受内压p作用，现讨论其轴向应力、周向应力和径向应力。

在材料力学中，由于壁厚远小于直径，其横截面面积近似取为A=πDt，则其轴向应力为[7]：

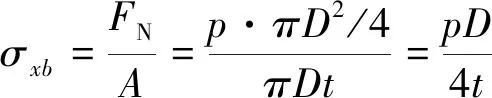
(2)周向应力和径向应力

1.2.2 薄壁圆筒受内压时应力相对误差分析

(1)薄壁圆筒周向应力相对误差分析

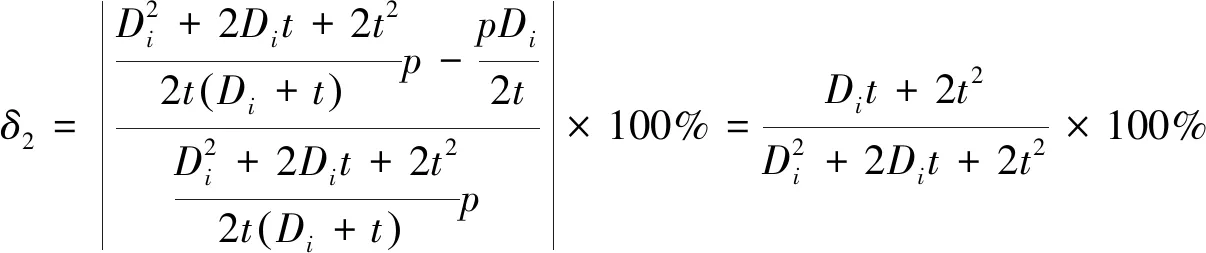
(2)薄壁圆筒轴向应力相对误差分析

(3)薄壁圆筒强度理论等效应力相对误差分析

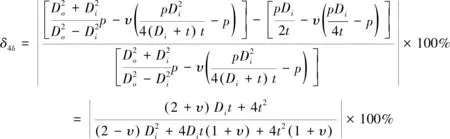
在满足薄壁圆筒的前提下，以碳钢为例，取材料的泊松比υ=0.3，δ4b的最大相对误差(即Di=20t时)为6.336%。

在满足薄壁圆筒的前提下，δ4c的最大相对误差(即Di=20t时)为4.545%。

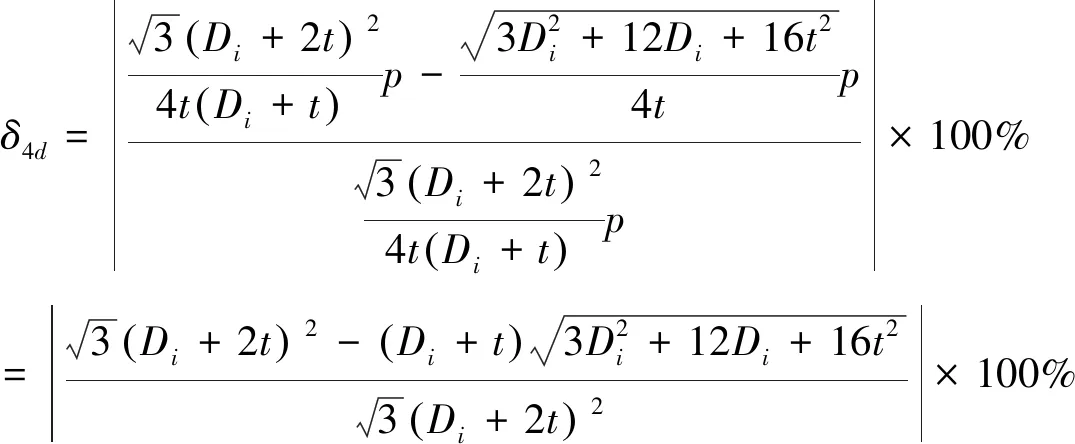
在满足薄壁圆筒的前提下，δ4d的最大相对误差(即Di=20t时)为4.414%。

现讨论式(6)、(11)中直径取不同的直径所引起的最大相对误差(即Di=20t时)如表2所示(在计算δ4b时泊松比υ=0.3)。

表2 薄壁圆筒受内压材料力学中近似公式中直径取不同的直径引起的相对误差

由表2可以看出：在计算轴向应力时，取内径最为合理，如取平均直径和外径，其相对误差远大于5%，是不合理的；在计算周向应力时，材料力学中取平均直径时相对误差最小，也最为合理，如取内径和外径是其相对误差仍小于5%，仍可取；在计算等效应力时，取平均直径相对误差最小，如取内径和外径，除第二强度理论等效应力取内径时的相对误差大于5%以外，其它等效应力的相对误差均小于5%，仍可取。取平均直径相对误差最小的主要原因是薄壁圆筒受内压时内表面上危险点的三个主应力中σ1为周向应力，而且周向应的绝对值远大于其它两个主应力，因此周向应力的相对误差起主导作用，通过分析周向应力在取平均直径时相对误差较小，仅为0.226%，因此，薄壁圆筒受内压在计算等效应力时取平均直径更为合理。