基于特征选择的数据驱动软测量方法

董 泽，贾 昊，姜 炜

基于特征选择的数据驱动软测量方法

董 泽1,2，贾 昊1,2，姜 炜1

（1.华北电力大学河北省发电过程仿真与优化控制技术创新中心，河北 保定 071003；2.华北电力大学控制与计算机工程学院，北京 102206）

由于测量环境恶劣，分析仪器成本昂贵，测量延迟大，发电机组一些关键参数难以实现在线测量。本文提出一种基于皮尔森相关系数和最小角回归算法相结合的特征选择方法，并以此为基础建立电厂烟气含氧量软测量模型。首先，根据机理分析确定烟气含氧量模型的初始输入变量，使用皮尔森相关系数对多测点数据进行数据融合；然后，使用最小角回归算法对输入变量进行特征选择，引入高斯过程回归（GPR）模型建立了烟气含氧量的软测量模型；最后将该模型用于某超超临界1 000 MW机组实际稳定工况数据进行仿真。结果表明：该模型预测结果与实测值误差较小，模型精度较高；使用该特征选择方法可以有效减少模型二次变量数量，降低模型输入复杂度，提高计算效率，同时可以改善模型的泛化能力，提高软测量的静态准确度。

软测量；数据融合；特征选择；皮尔森相关系数；最小角回归；高斯过程回归；烟气含氧量

在现代工业生产过程中，为了实现节能和效益最大化，及时对生产过程中的重要参数进行监测和控制具有重要意义。然而，在实际生产过程中，由于测量环境恶劣、分析仪器成本昂贵、测量延迟大等原因，使得这些参数大多难以在线测量。20世纪90年代以来，软测量技术[1]快速发展，逐渐成为解决以上问题的有效途径之一。软测量技术是一种利用易于测量的变量来建立预测模型估计难以测量变量的方法，这可以为过程监控、优化和控制提供所需的重要实时信息[2-3]。目前，软测量技术已经在热工领域取得了一些成功应用[4]。

与传统的机理建模方法相比，数据驱动软测量建模方法不需要先验知识和运行经验，完全使用历史数据建立预测模型。随着数据驱动建模方法的快速发展，很多多变量统计方法和机器学习方法应用在软测量上，如主成分回归（PCR）[5]、偏最小二乘回归（PLSR）[6]、人工神经网络（ANN）[7]和支持向量机（SVM）[8]等方法。

在软测量方法应用中，通常会有很多候选输入变量。特征选择可以减少输入变量的个数，减少模型的复杂性，同时可以减少过度拟合，提高模型精度，进而减少模型开发时间，提高模型性能。目前常见的特征选择方法有主成分分析法（PCA）[9]、互信息法（MI）[10]、偏最小二乘法（PLS）[11]。

在火电机组中，烟气含氧量可以反映机组的经济运行情况，是确保锅炉燃烧优化控制的主要因素之一。目前在电厂实际生产过程中，主要采用氧化锆氧量分析仪或使用软测量方法对烟气含氧量进行测量。氧化锆氧量分析仪存在维护成本高、寿命短且测量结果滞后大等缺点，其测量效果并不十分理想。目前已有一些软测量方法应用在火电厂烟气含氧量的测量上[12-13]。本文提出一种基于皮尔森相关系数和最小角回归算法相结合的变量筛选算法，以此确定软测量建模过程中的输入变量，并通过高斯过程回归方法建立烟气含氧量的软测量模型。采用某火电厂历史数据对所提方法进行测试，取得了良好的测量效果。

1 多测点数据融合与特征提取

1.1 多测点数据融合

目前对于火电厂热工系统而言，由于其具有设计参数高、容量大、生产过程恶劣等特点，对传感器有很高要求。为了保证系统安全，往往需要多路传感器对测点进行监测。多测点之间往往具有很强的线性关系，如果对该测量结果不进行处理直接作为输入变量对系统进行软测量建模，不但会增加计算量，还会导致共线性问题。

使用皮尔森相关系数法对多测点数据进行相关性分析，得到各传感器数据之间的拟合权值，将多测点数据进行融合。该方法比传统的求取多个传感器的算术平均值方法更加可靠、准确，物理意义也可以得到更好的说明。皮尔逊相关系数定义为2个变量之间的协方差和标准差之比：

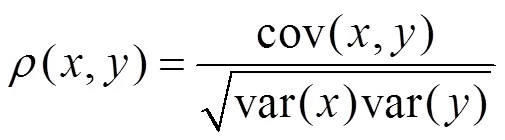
式中，cov()为与的协方差，var()和var()分别为和的方差。

由式(2)得到对应的第个变量的权重

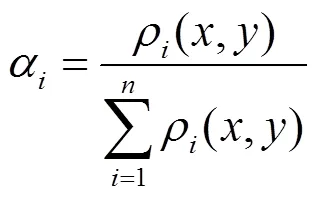
式中为对应的第个变量的权重。

1.2 最小角回归算法

最小角回归（LARS）算法[14]是一种线性回归方法，可用于高维数据的特征选择。相比于使用PLS方法做特征选择，LARS方法的可解释性更强。该方法首先构造一阶惩罚函数确定某些变量的系数为0，将其作为无效变量并删除，由此获得解释力强的模型。其优化目标可表示为：

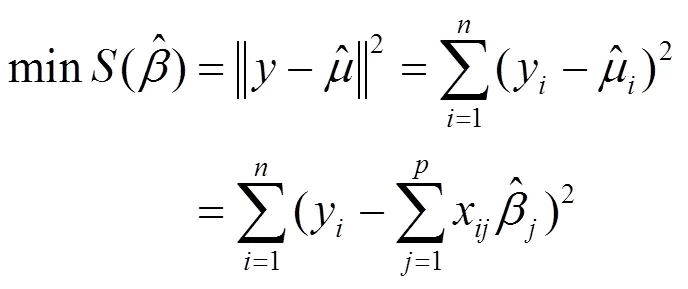
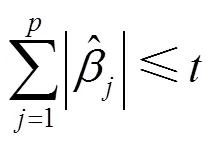
LARS算法在求解上述问题的基本思想是：首先将所有自变量的系数置0，找出与因变量相关性最大的自变量x。然后沿着x方向按照某个步长前进，直到可以选择出另一个和x都与当前残差具有相同相关性的变量x。然后沿x与x的角平分线的方向移动，直到找到另一个和(x x)都与残差相关性相同的变量l。由此类推，直至选择出所有所需变量。

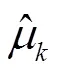
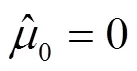
2）令=+1，当前相关系数记为

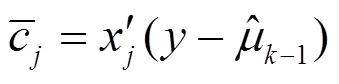
3）分别计算

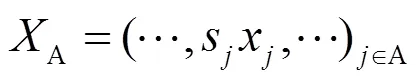
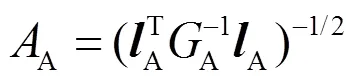
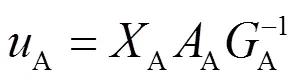
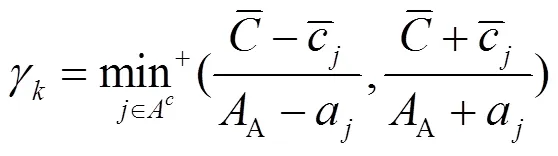
5）重复2)—4)步，直到选到所需变量个数为止。

2 高斯过程回归基本原理

2.1 高斯过程回归

高斯过程回归模型是一种基于贝叶斯统计理论的非参数概率模型[16]，其性质完全由均值和协方差确定，即：

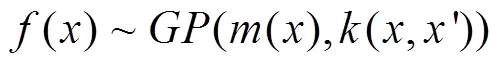
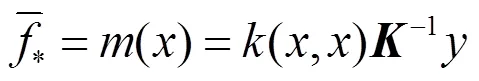
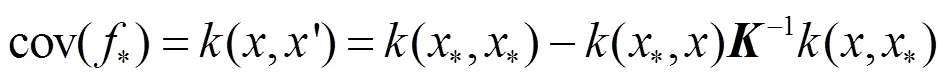
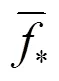
对于回归问题，考虑如下模型：

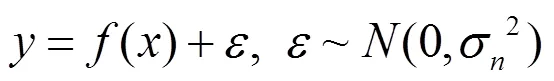
式中，为输入样本点的总数，为函数值，为均值为0方差为的白噪声。

由此得到的先验分布

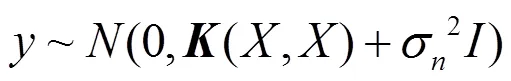
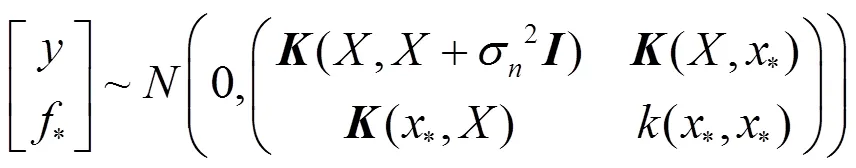
式中，(,)==(k)为×阶正定且对称的协方差矩阵，矩阵元素k=(x,x)为x和x之间的相关性，(,*) =(*,)T为测试点x与训练集输入之间的×1阶协方差矩阵，为维单位矩阵。

由此得出预测值f的后验分布：

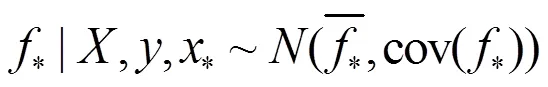
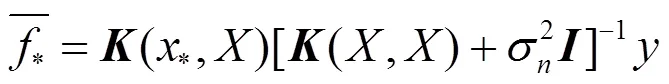
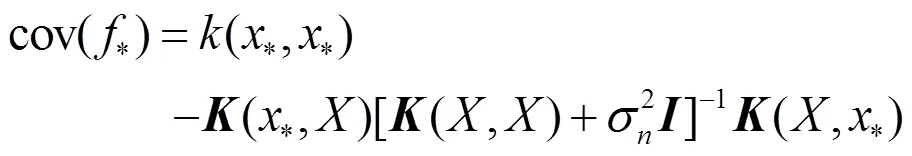
2.2 高斯过程训练

要建立一个高斯过程回归（GPR）模型首先需要选择模型的协方差函数，求取其中的协方差矩阵。一般选用高斯核函数作为协方差函数，即

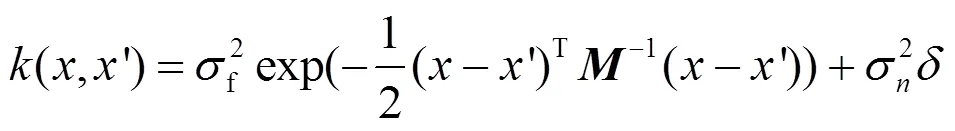
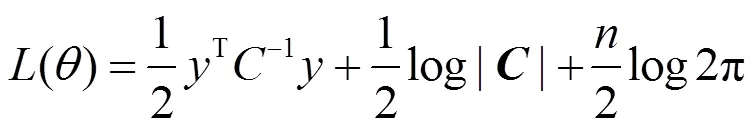
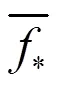
2.3 Pc-lars-GPR模型结构

本文提出的软测量建模过程如图1所示。首先，通过机理分析选择相关输入变量，得到原始输入变量集(1,2,,x)，为原始输入变量个数。然后通过计算多测点变量之间的皮尔森相关系数，确定变量权重，对多测点变量进行数据融合，得到输入变量集(1,2,,X)，为融合后输入变量个数。使用LARS算法找到输入变量集中各变量对应的权重系数集(1,2,,)。根据输入变量集和权重系数集，得到GPR模型最终的输入数据集(11,22,,X)。

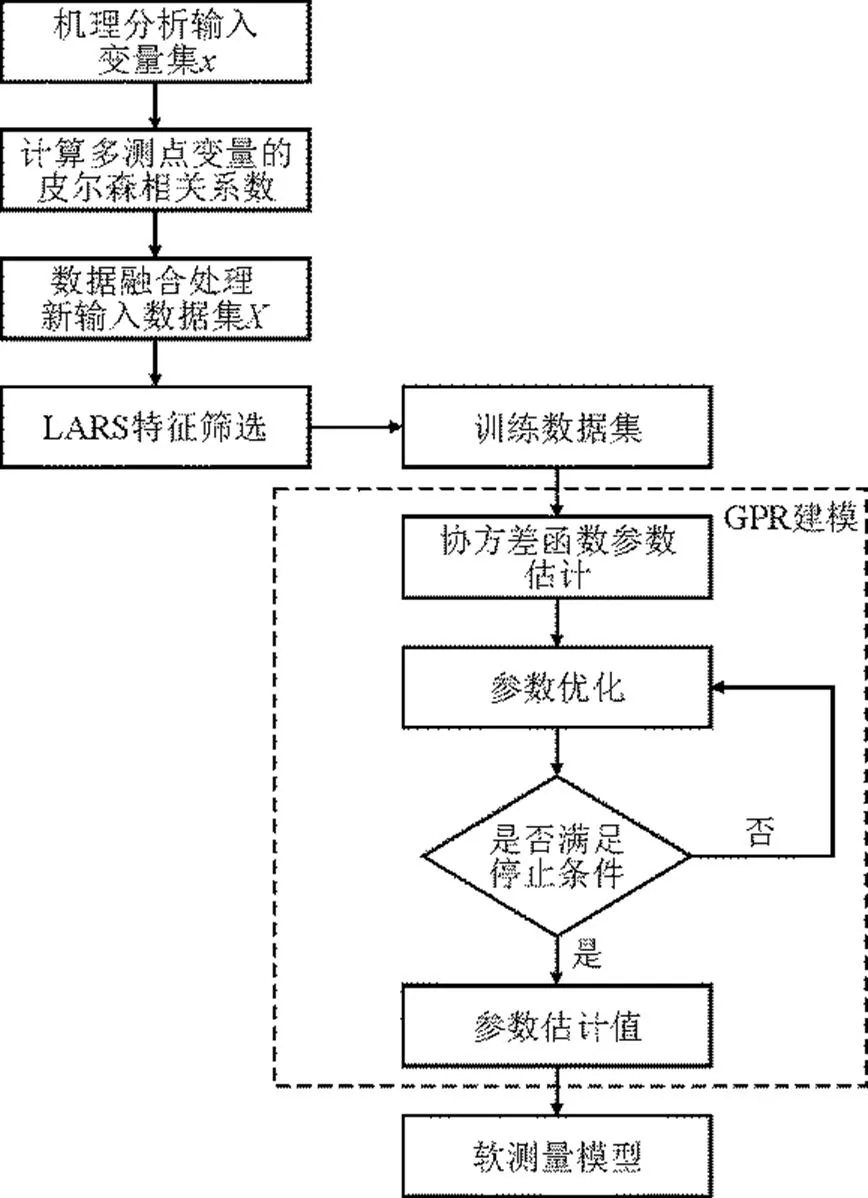
图1 Pc-lars-GPR模型

3 烟气含氧量软测量建模

烟气氧含量是与锅炉效率和经济燃烧密切相关的主要指标，但由于恶劣的工作条件和硬件传感器的高维护成本，很难实现在线精确测量。由于锅炉炉膛漏风、煤质变化和燃料不完全燃烧等因素对烟气含氧量的影响较大，因此选取能够反映负荷、燃料、风量等方面的变量作为辅助变量。根据机理分析并结合文献[17]中使用的变量，选择与烟气含氧量密切相关的25个过程变量作为二次变量，分别为主蒸汽压力1、主蒸汽温度2、炉膛负压3、总风量4、发电机有功功率5、给水流量6、总燃料量7、送风机A/B挡板开度89、引风机A/B挡板开度1011、送风机A/B电流1213、引风机A/B电流1415、空气预热器出口A1/A2/A3/ B1/B2/B3烟气温度1621、引风机出口A/B烟气温度2223、送风机入口A/B风量2425。输出变量为锅炉A/B两侧烟道中的烟气含氧量12。

采用某电厂超超临界1 000 MW二次再热机组的实际运行数据验证本文方法的有效性。从该电厂DCS选取机组负荷变化跨度较大(600~1 000 MW)的1个月运行数据，采样间隔设定为30 s，对其稳定工况下的烟气含氧量软测量建模。筛选具有良好工况代表性的稳态数据，采用文献[18]介绍的稳态检测方法，以机组负荷、主蒸汽压力、主蒸汽温度作为判定变量，筛选出975组稳态数据。使用其中650组数据作为训练样本，另外325组数据作为测试样本。

在训练模型前，首先对所有数据进行清洗和预处理，剔除离群点。然后将训练样本归一化到[-1,1]范围内，在得到输出后再进行反归一化处理。由于对输出1和2建立软测量模型所用的方法相同，仅以输出1为例，验证本文方法。

3.1 多测点数据融合

从二次变量集可以看出存在多测点变量，分别计算变量89、1011、1213、1415、1621、2223、2425的皮尔森相关系数，并用1.1节的方法对相关输入变量进行加权处理，从而得到新的输入数据集。以变量1621为例计算其皮尔森相关系数，计算结果见表1。

表1 多测点变量相关系数

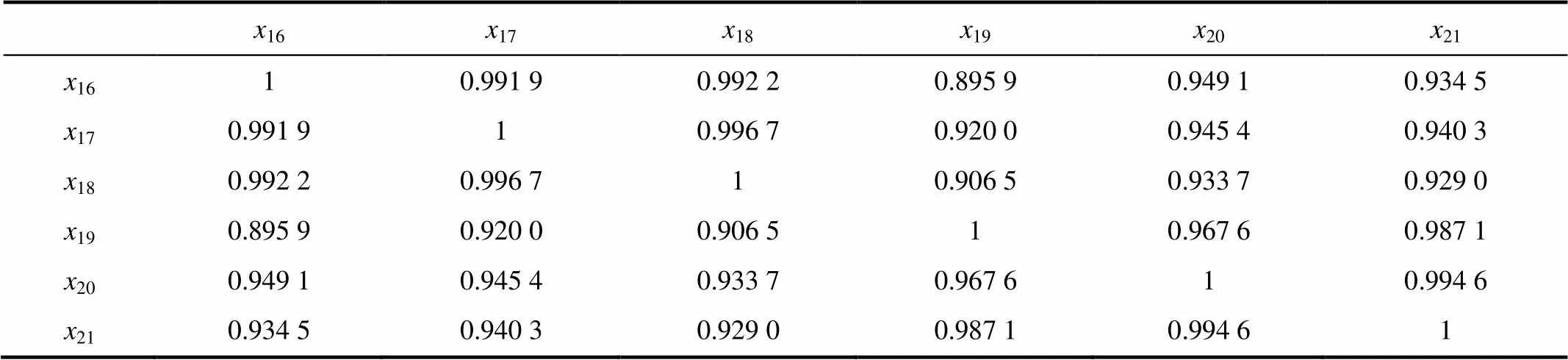
Tab.1 The correlation coefficient of multi-point variables

由表1可知变量间存在很强的线性相关性。当有测点存在故障时，其相关性系数将趋于零，则其对应的权重系数也趋于零，变量的修正值将不受故障点影响。因此，在建立烟气含氧量模型之前对多测点数据进行数据融合，不但可以降低输入变量，还有利于提高数据的准确性。

通过对多测点变量数值进行加权融合，得到新的输入变量集。新变量集包含14个变量，分别为主蒸汽压力1、主蒸汽温度2、炉膛负压3、总风量4、发电机有功功率5、给水流量6、总燃料量7、送风机挡板开度8、引风机挡板开度9、送风机电流10、引风机电流11、空气预热器出口烟气温度12、引风机出口烟气温度13、送风机入口风量14。

3.2 输入参数选取与特征系数计算

使用LARS算法计算数据融合得到的输入变量集的特征系数，从而得到GPR软测量建模的输入数据集。以预测输出1为例，计算各输入变量的系数。迭代次数与系数的关系及各输入变量权重系数分别如图2和表2所示。

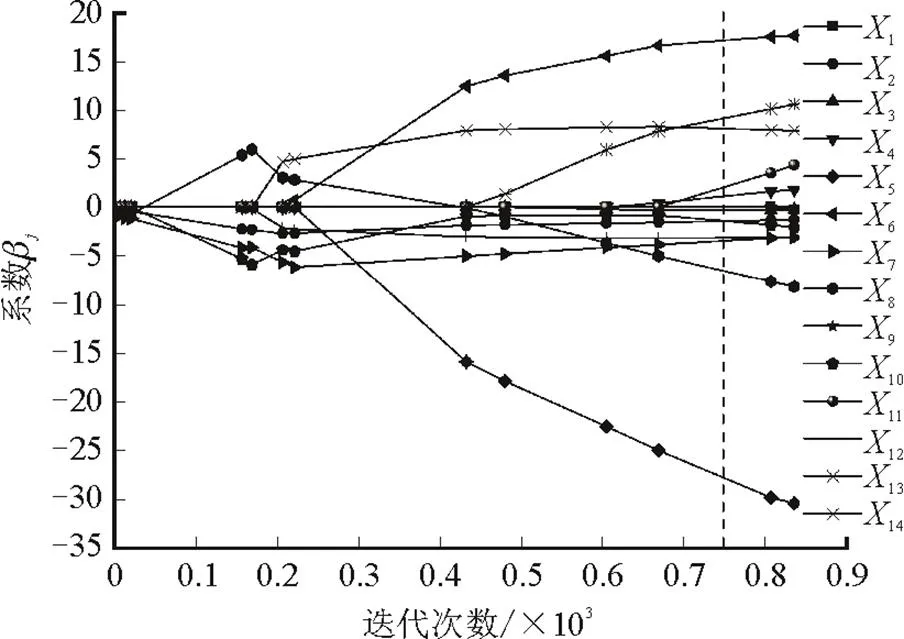
图2 迭代次数与系数的关系

表2 输入变量权重系数

Tab.2 The weight coefficients of the input variables

由表2可知，通过使用LARS算法对输入数据集进行分析，确定特征变量主蒸汽压力1和引风机挡板开度9对烟气含氧量软测量建模的影响较小，故将这2个变量从输入数据集中剔除。由给出的特征系数，得到最终输入数据集。

3.3 模型验证与比较

为了对比验证建模效果，本文同时采用核偏最小二乘（KPLS）、最小二乘支持向量机（LSSVM）作为对比建模方法，同时与是否采用本文提出的特征选择方法做对比，所有建模方法的核函数均采用高斯核函数。

本文分别使用均方根误差RMSE、平均相对误差MRE和决定系数2作为模型的评价指标，验证模型性能。各指标计算公式为

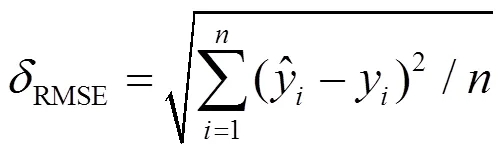
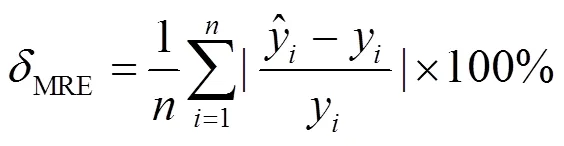
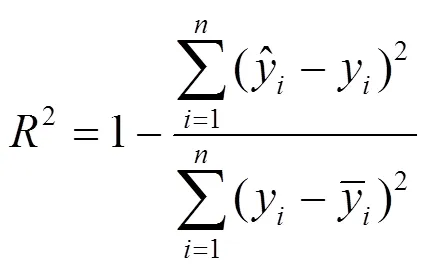
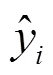
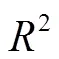
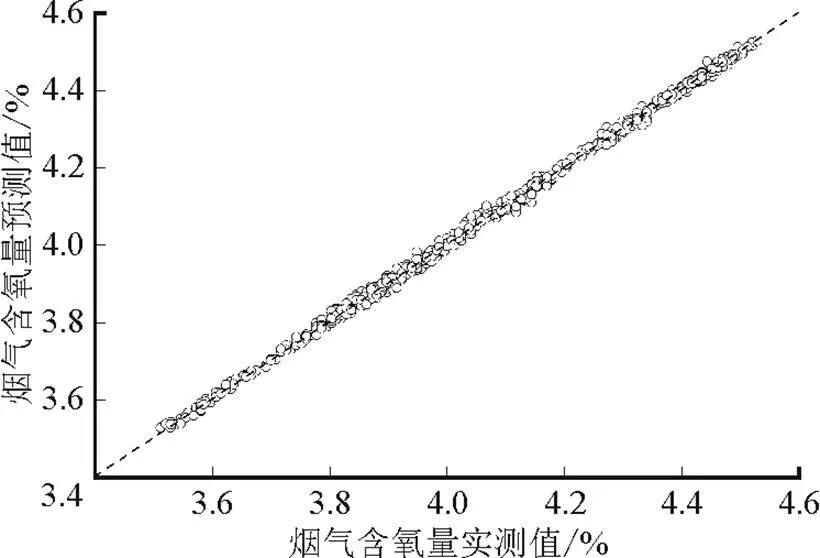
图3 训练样本实测值与预测值对比

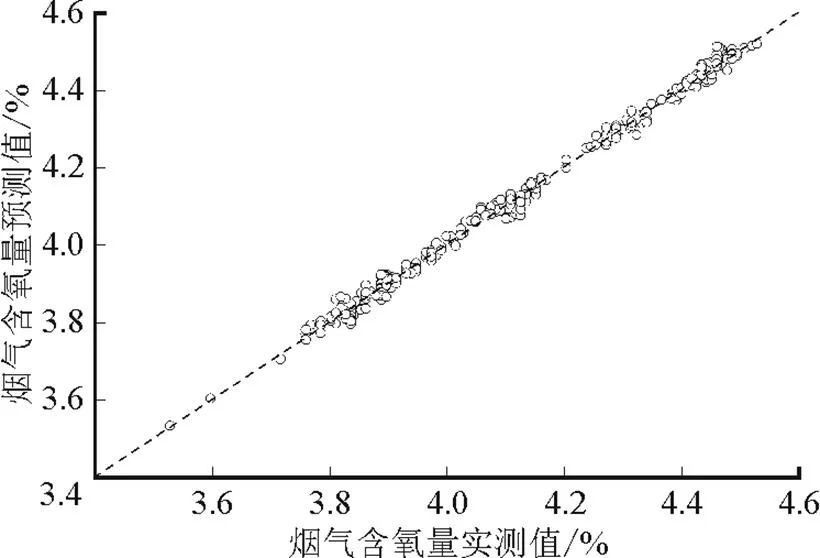
图4 测试样本实测值与预测值对比

为了更直观地展示Pc-lars-GPR模型的泛化能力，图5使用点划线对实测值与预测值做对比。由图5可知，预测值与实测值非常接近，且处于95%置信度区间内，证明该模型具有良好的性能。此外，对3种模型以及是否采用本文提出的特征选择方法做对比，各模型误差对比结果如表3和图6—图7所示。图6是从训练样本的角度对算法性能进行比较。由图6a）可见，比较KPLS、LSSVM和GPR对训练样本的预测误差，GPR模型对训练样本的拟合程度最好，RMSE和MRE指标最小，LSSVM模型的效果次之，KPLS模型的效果最差。与KPLS和LSSVM建模方法相比，GPR模型参数优化相对容易，因此模型的精确性较好。KPLS方法是在PLS方法基础上通过使用高斯核函数实现非线性建模。由于PLS本身是一种线性建模方法，尽管采用了核函数，其对处理非线性问题仍存在一定误差。如图6b）所示，通过在建模前使用特征选择算法对输入变量进行筛选，3种建模方法的建模误差都有一定程度降低。

图7为测试样本各模型的预测误差，主要考察模型的泛化能力。由图7a)可见，GPR表现最好，KPLS表现最差，说明GPR建模方法不但建模精度较好，而且模型泛化能力优良。由图7b)可见，采用特征选择算法对输入变量进行筛选，也能提高模型的泛化能力。

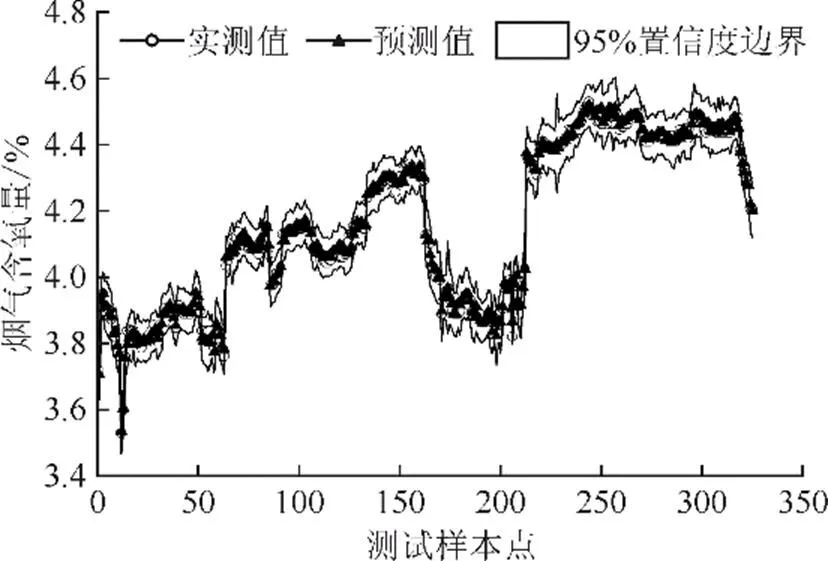
图5 实测值与预测值对比

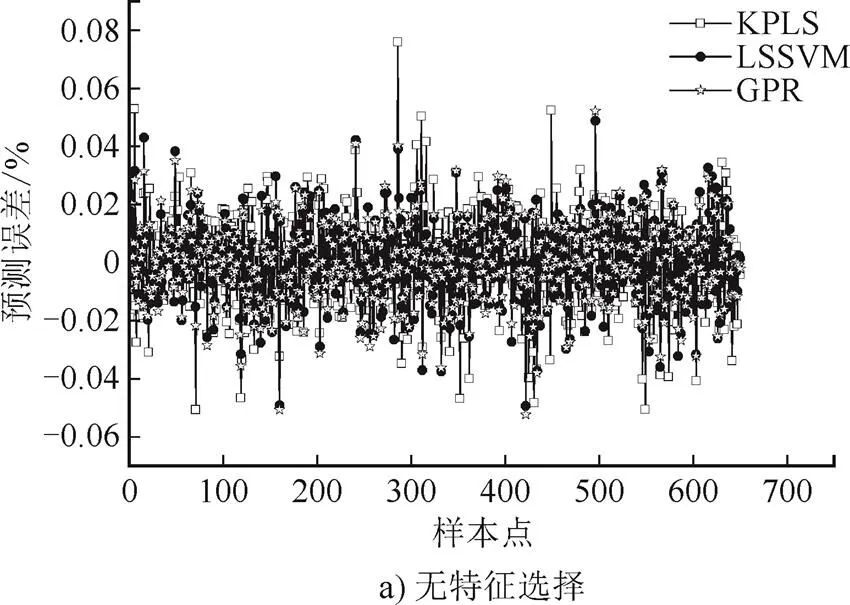
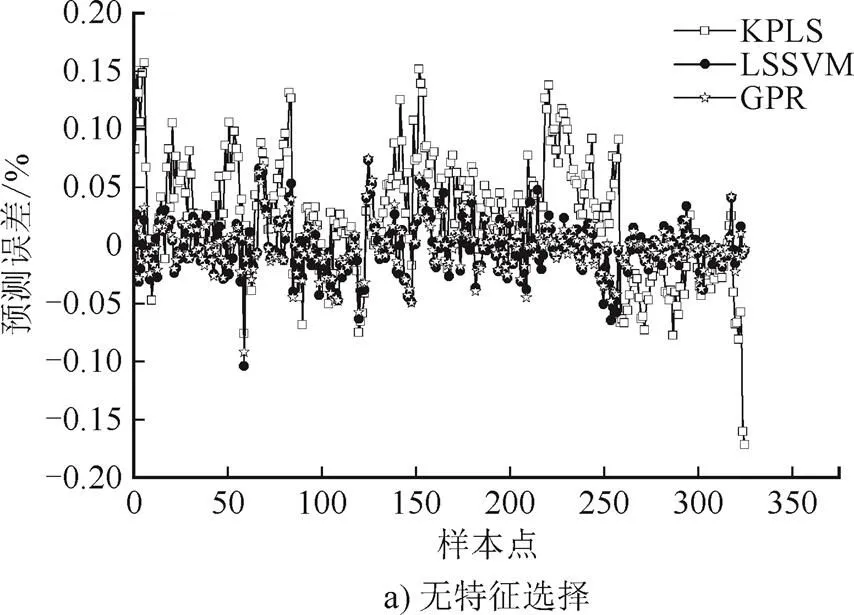
表3 各模型性能对比

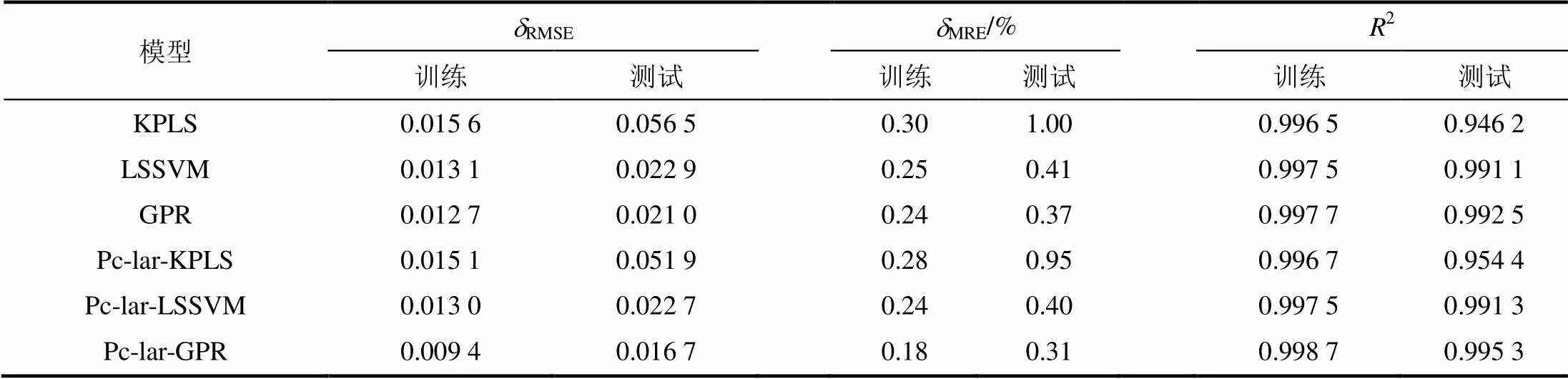
Tab.3 Performance comparison of each model

4 结 论

1）采用皮尔森相关系数对多测点进行数据融合，得到的测量结果比多个测点的算术平均值更准确，可靠性更高。同时该方法减少了建模计算量，减轻了模型共线性问题，提高了建模精度。

2）通过采用LARS算法得到输入变量的特征系数，由此得到最终的输入变量集。该方法可以有效减少建模所需的输入变量个数，降低输入变量的维度，减少计算量。

3）将本文提出Pc-lars-GPR烟气含氧量模型应用于某超超临界1 000 MW机组的烟气含氧量软测量，结果表明该模型误差较小，且其静态准确度和泛化性能均可满足软测量要求。

［1］ KADLEC P, GRBIĆ R, GABRYS B. Review of adaptation mechanisms for data-driven soft sensors[J]. Computers & Chemical Engineering, 2011, 35(1): 1-24.

［2］ KHATIBISEPEHR S, HUANG B, KHARE S. Design of inferential sensors in the process industry: a review of Bayesian methods[J]. Journal of Process Control, 2013, 23(10): 1575-1596.

［3］ GE Z. Mixture Bayesian regularization of PCR model and soft sensing application[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4336-4343.

［4］ 韩璞, 乔弘, 王东风, 等. 火电厂热工参数软测量技术的发展和现状[J]. 仪器仪表学报, 2007, 28(6): 1139-1146.

HAN Pu, QIAO Hong, WANG Dongfeng, et al. Development and current status of thermal parameter soft-sensing technique in power plant[J]. Chinese Journal of Scientific Instrument, 2007, 28(6): 1139-1146.

［5］ YUAN X, GE Z, SONG Z, et al. Soft sensor modeling of nonlinear industrial processes based on weighted probabilistic projection regression[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(4): 837-845.

［6］ GALICIA H J, HE Q P, WANG J. A reduced order soft sensor approach and its application to a continuous digester[J]. Journal of Process Control, 2011, 21(4): 489-500.

［7］ ROGINA A, ŠIŠKO I, MOHLER I, et al. Soft sensor for continuous product quality estimation (in crude distillation unit)[J]. Chemical Engineering Research and Design, 2011, 89(10): 2070-2077.

［8］ 李建强, 赵凯, 牛成林, 等. 基于GA-SVM的电站锅炉烟气含氧量软测量模型[J]. 热力发电, 2017, 46(4): 63-69.

LI Jianqiang, ZHAO Kai, NIU Chenglin, et al. GA-SVM-based soft-sensor model for oxygen content in flue gas of utility boilers[J]. Thermal Power Generation, 2017, 46(4): 63-69.

［9］ 金秀章, 韩超. KPCA-LSSVM在磨煤机一次风量预测中的应用[J]. 自动化仪表, 2015, 36(3): 62-67.

JIN Xiuzhang, HAN Chao. Application of KPCA-LSSVM in prediction of the primary air flow of pulverizer[J]. Process Automation Instrumentation, 2015, 36(3): 62-67.

［10］ 刘吉臻, 秦天牧, 杨婷婷, 等. 基于偏互信息的变量选择方法及其在火电厂SCR系统建模中的应用[J]. 中国电机工程学报, 2016, 36(9): 2438-2443.

LIU Jizhen, QIN Tianmu, YANG Tingting, et al. Variable selection method based on partial mutual information and its application in power plant SCR system modeling[J]. Proceedings of the CSEE, 2016, 36(9): 2438-2443.

［11］吕游, 刘吉臻, 杨婷婷, 等. 基于PLS特征提取和LS-SVM结合的NO排放特性建模[J]. 仪器仪表学报, 2013, 34(11): 2418-2424.

LV You, LIU Jizhen, YANG Tingting, et al. NOemission characteristic modeling based on feature extraction using PLS and LS-SVM[J]. Chinese Journal of Scientific Instrument, 2013, 34(11): 2418-2424.

［12］ 李建强, 张莹莹, 牛成林. 基于PSO-LSSVM模型的火电厂烟气含氧量预测[J]. 热能动力工程, 2018, 33(7): 49-55.

LI Jianqiang, ZHANG Yingying, NIU Chenglin. Prediction of the oxygen content in flue gas of power plant based on PSO-LSSVM model[J]. Journal of Engineering for Thermal Energy and Power, 2018, 33(7): 49-55.

［13］ 贺桂林, 王富强, 张秋生, 等. 基于非参数组合的电厂含氧量软测量模型[J]. 热力发电, 2018, 47(4): 55-62.

HE Guilin, WANG Fuqiang, ZHANG Qiusheng, et al. Soft measurement model of oxygen content based on the nonparametric combination for power plants[J]. Thermal Power Generation, 2018, 47(4): 55-62.

［14］ EFRON B, HASTIE T, JOHNSTONE I, et al. Least angle regression[J]. The Annals of Statistics, 2004, 32(2): 407-499.

［15］ 颜胜科, 杨辉华, 胡百超, 等. 基于最小角回归与GA-PLS的NIR光谱变量选择方法[J]. 光谱学与光谱分析, 2017, 37(6): 1733-1738.

YAN Shengke, YANG Huihua, HU Baichao, et al. Variable selection method of NIR spectroscopy based on least angle regression and GA-PLS[J]. Spectroscopy and Spectral Analysis, 2017, 37(6): 1733-1738.

［16］ RASMUSSEN C E. Gaussian processes in machine learning[M]. Springer, Berlin, Heidelberg: Advanced Lectures on Machine Learning, 2004: 63-71.

［17］YAN W, TANG D, LIN Y. A data-driven soft sensor modeling method based on deep learning and its application[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5): 4237-4245.

［18］ 贾昊, 董泽, 闫来清. 基于信号分解和统计假设检验的稳态检测方法[J]. 仪器仪表学报, 2018, 39(10): 150-157.

JIA Hao, DONG Ze, YAN Laiqing. Steady-state detection method based on signal decomposition and statistical hypothesis test[J]. Chinese Journal of Scientific Instrument, 2018, 39(10): 150-157.

Data-driven soft sensor modeling method based on feature selection

DONG Ze1,2, JIA Hao1,2, JIANG Wei1

(1. Hebei Technology Innovation Center of Simulation & Optimized Control for Power Generation, North China Electric Power University, Baoding 071003, China; 2. School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China)

Due to poor measurement environment, expensive analytical instruments and large measurement delay, some key variables of power generating units are difficult to realize on-line measurement. To solve this problem, a feature selection method based on the Pearson correlation coefficient and the least angle regression algorithm (LARS) is presented. On this basis, a soft sensing model of oxygen content in flue gas of power plants is established. Firstly, the initial variables of oxygen content in flue gas are determined according to the mechanism study, and the Pearson correlation coefficient is used to fuse the data of multiple measurement points. Then, the least angle regression algorithm is used to select the input variables, and the soft sensor model of oxygen content in flue gas is established by introducing the Gauss process regression (GPR) model. Finally, this model is applied to simulate the actual steady condition data of an ultra supercritical 1 000 MW unit. The results show that, the predicted results have little error with the actually measured values, and the precision of the model is higher. Applying this feature selection method can effectively reduce the number of the secondary variables used in modeling, decrease the input complexity of the model and improve the calculation efficiency. Moreover, it can enhance the static accuracy and generalization ability of the flue gas oxygen content model.

soft sensing, data fusion, feature selection, Pearson correlation coefficient, least angle regression, Gauss process regression, oxygen content in flue gas

TP274.2

A

10.19666/j.rlfd.201901004

2019-01-16

河北省自然科学基金项目(E2018502111)；中央高校基本科研业务费专项资金资助(2018QN096)

Supported by：Natural Science Foundation of Hebei Province (E2018502111); Fundamental Research Funds for the Central Universities (2018QN096)

董泽(1970—)，博士，教授，主要研究方向为大型火电机组建模理论与方法、智能控制理论及应用，dongze33@126.com。

贾昊(1988—)，博士研究生，主要研究方向为大型火电机组历史数据挖掘与建模，Jiah_paper@163.com。

董泽, 贾昊, 姜炜. 基于特征选择的数据驱动软测量方法[J]. 热力发电, 2019, 48(9): 83-89. DONG Ze, JIA Hao, JIANG Wei. Data-driven soft sensor modeling method based on feature selection[J]. Thermal Power Generation, 2019, 48(9): 83-89.

（责任编辑 杜亚勤）