基于量子蜂群聚类的T-S模糊建模在智能发电运行控制中应用

侯国莲，弓林娟

基于量子蜂群聚类的T-S模糊建模在智能发电运行控制中应用

侯国莲，弓林娟

（华北电力大学控制与计算机工程学院，北京 102206）

建立发电机组在大范围变工况下的精确模型是智能发电运行控制中最为基础也是至关重要的环节。为提高建模过程的快速性以及所得模型的精确性和通用性，本文提出了一种基于量子蜂群聚类的新型T-S模糊建模方法。该方法首先将量子蜂群作为聚类算法进行前提部分辨识，不仅通过量子概念的引入提高了聚类速度，而且通过决策常数和数据空间约束消除了聚类过程中人为设定聚类个数的主观性。其次基于前提部分辨识结果，在结论部分辨识中通过指数加权最小二乘法保证了局部模型参数辨识过程的简便性和精确性。最后以超超临界机组协调控制系统的建模为例，探讨了所提出算法在智能发电运行控制系统发电机组建模中的应用。仿真结果表明，该算法不仅保证了建模过程的快速性，还使得辨识所得模型在机组大范围变工况下始终保持较高精度，表现出良好的通用性和适应性。

智能发电；运行控制；量子蜂群聚类；T-S模糊建模；协调控制系统；大范围变工况；模型辨识；超超临界机组

随着大数据、深度学习、数据挖掘、故障诊断等先进技术的飞速发展，“智能发电”已经成为未来电力发展的必然趋势[1]。对于“智能发电”这一概念，刘吉臻等对其做了概括性的定义[2]，并在文献[3]中对智能发电厂的构架及其特点做了解析。智能发电厂是由智能设备层、智能控制层、智能生产监督层和智能管理层4层组成的一个智能管控一体化结构。其中智能控制层通过多种技术手段的结合进行发电系统的智能控制、多目标优化和数据分析，以实现能源利用效率最大化和污染物排放最小化，在整个智能电厂的安全稳定运行中发挥着重要作用。

智能发电运行控制主要由数据基础、智能算法和功能应用组成[4]。其中，数据基础是指实际发电过程的生产数据汇聚和计算中心；智能算法包括对生产过程的优化控制和数据分析；功能应用则包含智能诊断与预警、智能安全管控等功能群组。在这三部分中，数据基础服务于智能算法和功能应用，而功能应用则建立在智能算法的基础之上，因此，智能算法占据着三者中的核心地位。在智能算法中，优化控制保证机组在不同工况下都能克服自身非线性、强耦合等复杂特性的影响，并且抑制外界扰动以保证发电系统的稳定运行；而优化控制器的设计往往基于已知的对象模型。基于以上分析，鉴于发电机组模型在智能发电运行控制的重要性，本文将从模型辨识方法出发，讨论其在智能发电运行控制中的应用。

由于发电过程的复杂性，其被控对象一般具有非线性、不确定性和强耦合等特点[5]，传统的机理建模很难做到对其内部机理进行详尽的分析。另因在智能发电过程中可方便获取到机组的现场实际运行数据，因此发电机组的建模可选用基于数据的模型辨识方法。单一的最小二乘或子空间辨识等基于线性系统的建模方法难以达到系统全工况范围模型的精确辨识。T-S模糊辨识作为近年来蓬勃发展的智能建模方法，可利用If-Then语句描述系统输入输出间的非线性关系[6]，通过前提部分辨识和结论部分辨识的有机结合有效处理待建模对象的复杂特性，提高建模精度。在T-S模糊辨识中，首先根据数据相似性通过聚类算法进行数据集合的划分，然后在后件辨识中利用最小二乘等一般辨识方法基于各个聚类进行局部模型辨识，最后对各个局部模型输出进行模糊加权生成模型的全局输出。

针对火电机组机炉系统的模糊建模问题，文 献[7]的前提部分辨识中引入了Gaustafson Kessel （G-K）聚类方法，该方法通过数据间的协方差矩阵加权距离进行数据集子空间的划分，对多种形状的聚类空间具有良好的局部适应性，但聚类过程中聚类个数等需人为设定参数的存在增加了聚类结果的主观性。为解决这一问题，文献[8]中将阈值和决 策常数引入熵聚类算法中，使得聚类过程中可以 自动生成聚类个数和相应的聚类半径，大大提高了聚类过程的自主性，然而没有考虑熵聚类算法的快速性问题。除上述2种聚类方法外，模糊C均值（FCM）[9-10]和K均值[11-12]方法也被广泛应用于聚类过程中，并且保证了聚类速度，但是依然难以克服参数设置主观性和公式推导复杂性的问题。近年来迅速发展的遗传算法（GA）[13]、粒子群优化（PSO）算法[14]、猫群（CSO）算法[15]等仿生算法在控制优化和模型辨识中也取得了一些成功的应用，此类算法原理简单易懂，能以较低的计算复杂度达到精确的优化结果。文献[16]将量子的概念引入人工蜂群（ABC）算法中形成了新的量子人工蜂群（QABC）算法，不仅保证了ABC原有的搜索能力和范化能力，还从很大程度上提高了寻优速度。因此，本文尝试将QABC作为聚类算法引入T-S模糊建模的前件辨识，以提高辨识过程的快速性和所建模型的精确性。基于前提部分辨识结果，文献[17]通过子空间辨识（SID）方法进行了结论部分各个子模型的辨识，虽然可以从一定程度上反映系统内部状态，但是辨识过程中存在较多高维度的矩阵运算，不利于辨识过程快速性和建模结果精确性的提高。与此同时，指数加权最小二乘[8]、扩展遗忘因子递推最小二乘[18]等基于最小二乘的辨识算法也在T-S模糊建模后件辨识中展现出优良的效果。相较于SID，基于最小二乘的方法辨识所得模型具有更高的精度，且计算过程复杂度较低，因此，本文考虑用文献[8]中的指数加权最小二乘方法进行T-S模糊建模结论部分的辨识。

针对智能发电运行控制中发电机组的建模问题，本文提出一种基于QABC聚类的改进型T-S模糊建模方法。该方法首先在前件辨识中将QABC作为聚类算法以提高聚类过程的快速性，然后通过决策常数和数据空间约束的引入使聚类过程自动生成聚类个数和聚类半径，从而克服了聚类个数人为选定的主观性；在后件辨识中则通过指数加权最小二乘对各个子模型的受控自回归积分滑动平均（CARIMA）模型进行辨识。最后通过对超超临界单元机组机炉系统的建模，验证该方法辨识所得模型在机组大范围变工况下的适应性和精确性。

1 问题描述

智能发电运行控制首先通过数据基础、智能算法和功能应用对全厂的生产运行数据进行整合形成统一的数据平台；然后基于该平台提供智能算法及其应用环境进行被控对象的建模和系统控制优化，并通过对控制过程的计算进行数据分析；最后在功能应用部分与上层应用软件建立连接。由上文分析可知，发电机组建模是智能发电运行控制中非常重要的环节，能否为机组建立一个克服自身复杂特性，有效抑制外界扰动并自适应大范围变工况的模型成为亟待解决的问题。本文将从目前我国技术较为先进和成熟的超超临界单元机组出发，对其机炉协调系统的建模问题展开研究。

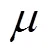
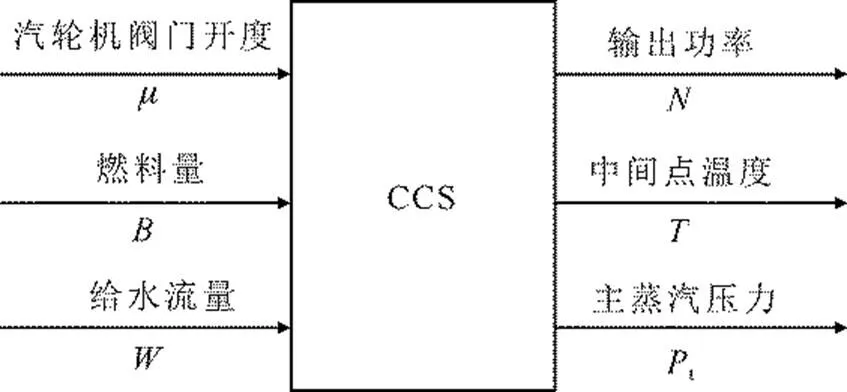
图1 CCS简化模型

2 基于QABC聚类的T-S模糊建模

2.1 T-S模糊模型结构

为便于复杂系统的建模和分析，一般将多入多出系统视为多个多入一出系统的组合，如图1中的三入三出CCS就可被划分为3个三入一出的系统。因此下文对辨识算法的描述中仅以单个多入单出系统为例进行说明。考虑到增量数据之间具有更强的线性关系[8]，给出如下T-S模糊模型的增量形式：

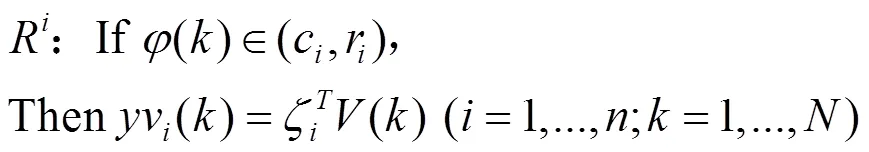
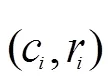
各增量计算公式如下：

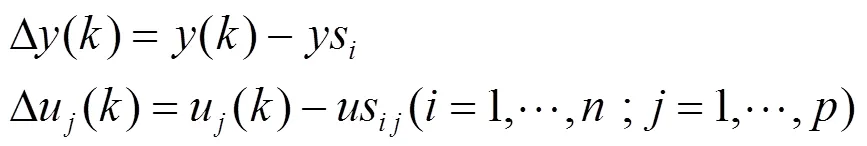
式中，us、ys为第个聚类中各输入输出变量的稳态点，在本文中视为第个聚类的聚类中心c。

由于yv只是得到的一个增量数据，因此需通过式(3)进行计算得到局部模型的实际输出：

最后，将以上各子模型输出按式(4)进行模糊加权，得到待辨识系统的全局输出：

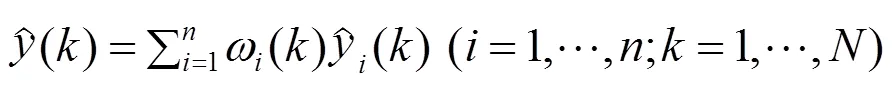
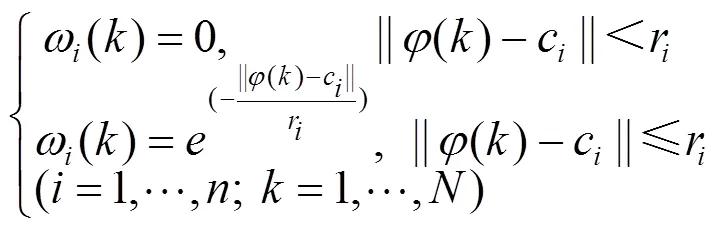
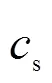
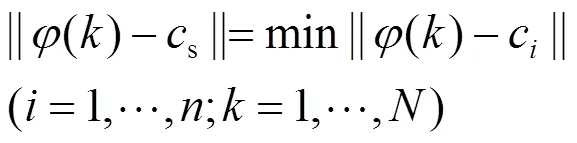
2.2 基于QABC聚类的前提部分辨识

前提部分辨识包括聚类个数的获得以及聚类中心和聚类半径的计算，考虑到QABC算法对搜索空间的遍历性，良好的范化能力以及计算快速性，在这个过程中通过QABC进行辨识数据的聚类划分。与此同时，为避免人为设定聚类个数的主观性，引入决策常数和数据空间约束自动进行聚类并生成相应的聚类个数以及聚类中心，然后通过计算得到聚类半径。

ABC算法是一种启发于蜜蜂觅食行为的仿生算法[20]，通过雇佣蜂、观察蜂和侦查蜂的紧密配合对蜜源位置不断进行寻优，直至找到较为理想的最优蜜源。该算法对搜索空间具有良好的遍历性，且表现出优越的泛化能力，但寻优速度过慢成为阻碍其发展的一大障碍。为解决这一问题，将量子的概念引入原有ABC中形成QABC，通过蜜源位置的量子编码和量子旋转位更新，使QABC在保证ABC原有优势的同时，大大提升收敛速度。本文在前提部分辨识过程中，将聚类中心视为蜜源进行数据聚类，具体过程如下。

1）初始化蜂群种群规模和蜜源个数同为c，最大迭代次数为，某一蜜源连续没有被更新的次数上限为Lim，则根据蜂群算法特点可得，蜂群中雇佣蜂、观察蜂和侦查蜂的个数均等于种群规模c。本文将C设为辨识过程广义输入向量的维度1+…+n+。

2）通过量子概率幅值对蜜源初始位置编码：

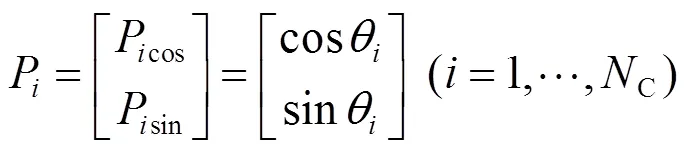
以上量子编码位对应的解空间向量表示如下：

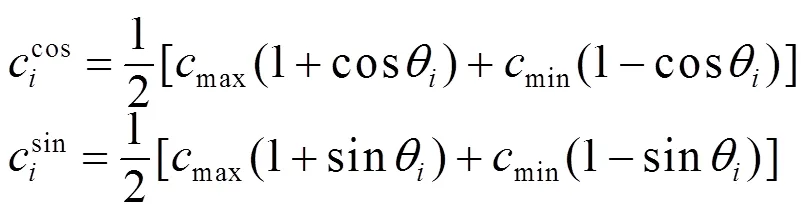
式中max,i=max()和min,i=min()分别代表聚类中心的上下界。

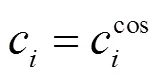
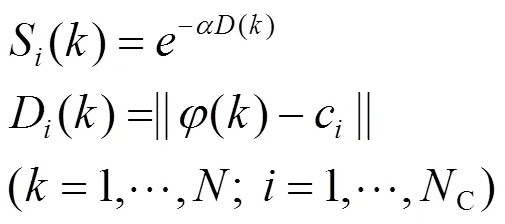
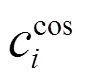
4）引入决策常数和数据空间约束d，若S()＞，则将该时刻的数据对其归入c代表的聚类中，并记该初始聚类中所有的数据对个数为c，若c＞d，接受该聚类，=+1，转到步骤5），否则，舍弃该聚类，转到步骤6）。

5）将以c为中心的聚类中所包含的数据对从原来数据对集合中移除，则剩下数据对个数为r=‒c；若r＜d，聚类过程结束，否则，转向步骤6）。

6）为每个雇佣蜂分配1个蜜源，通过以下量子旋转位更新蜜源位置即聚类中心：

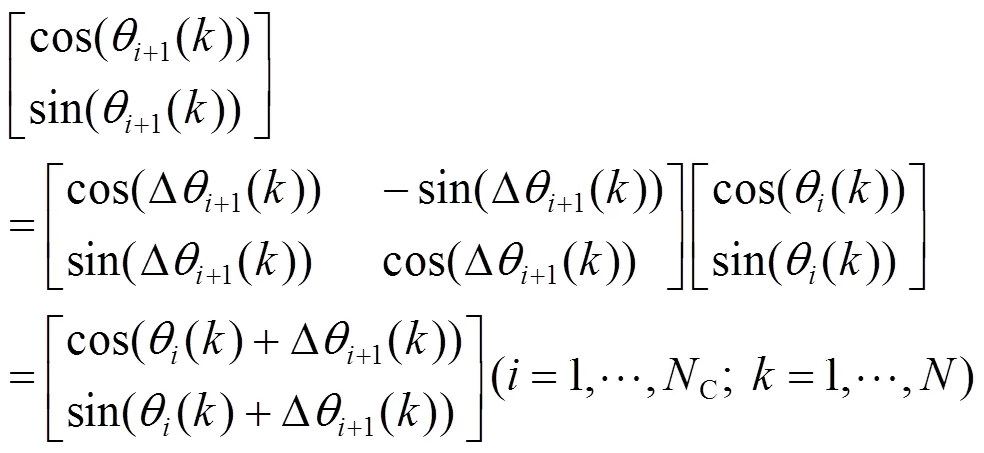
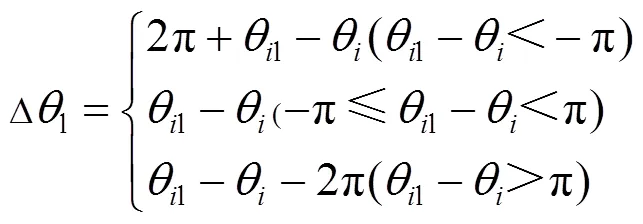
式中l为当前最优相角。

7）利用式(8)进行更新后的量子位解空间求解，计算当前聚类中心与输入向量的相似性进行贪婪选择，若新的蜜源优于前一个，则为每一个观察蜂分配一个蜜源返回步骤4）；否则，若该蜜源连续没有被更新的次数达到Lim，则该雇佣蜂转化为侦查蜂，重新进行蜜源搜索。

8）若满足步骤5）中聚类终止条件，或寻优达到QABC最大迭代次数，结束聚类；否则，返回步骤2）。

上述聚类过程结束后，可自动得到聚类个数和聚类半径，然后通过下式对聚类半径r(=1,…,)进行计算：

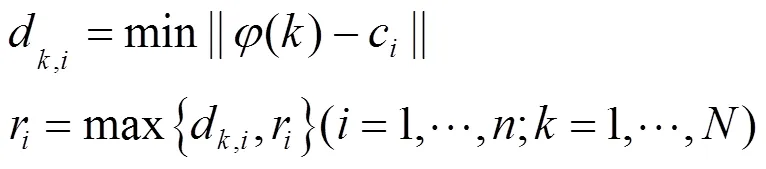
2.3 基于指数加权最小二乘的结论部分辨识

由于本文所用T-S模糊模型为增量结构，所以首先应根据聚类中心计算达到各输入输出变量的增量数据，然后通过以下指数加权最小二乘进行结论各局部模型参数的辨识。

1）矩阵的初始化：

其中在本文中取105。

2）通过如下递归公式得到模型参数向量：

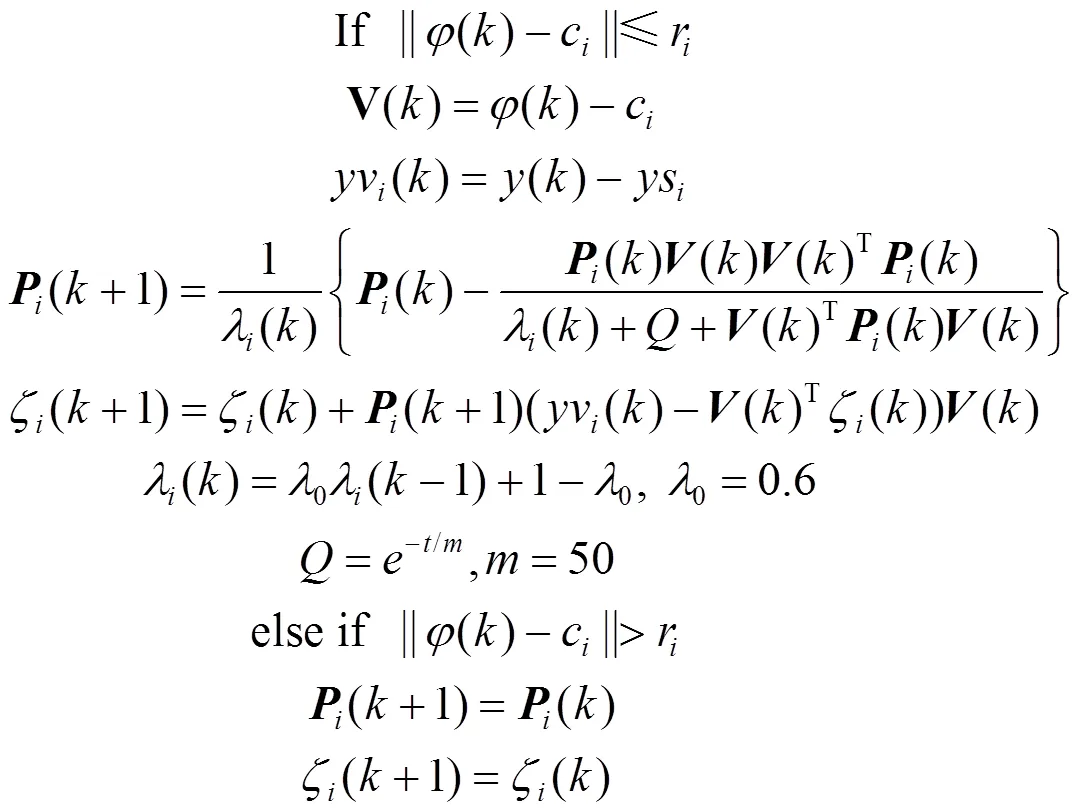
3）=+1，返回步骤2），直到=停止迭代，记录辨识所得模型参数。

3 应用仿真

作为智能发电运行控制中的重要环节，建模过程中得到模型的精确性和大范围工况内的通用性将直接影响整个机组的安全稳定运行。本文将基于发电机组CCS实际运行数据，通过对比实验验证本文所提出T-S模糊建模方法的快速性和有效性，以及辨识所得模型的精确性，最后通过大范围变工况测试该模型的通用性和适应性。

首先对基于QABC聚类的T-S模糊辨识算法的参数进行设置，结果见表1。

表1 基于QABC聚类的T-S模糊辨识算法参数设置

Tab.1 Parameter selections of the T-S fuzzy identification algorithm based on QABC clustering

其次对辨识数据进行选取。在建模数据的选择中应选择大范围变工况条件下的闭环数据，此类数据集可以尽可能多地覆盖机组运行工况点，并且数据变化快，幅度大，能保证持续激励。根据上述原则，本文选取泰州电厂超超临界1 000 MW机组的4 000组数据进行模型辨识，该段数据负荷变化范围为500~1 000 MW，采样间隔为3 s，输入变量数据如图2所示。

最后通过本文所提出方法对单元机组CCS模型进行辨识，并绘制模型输出与实际运行数据的拟合和误差曲线，结果如图3所示。图3的左半部分为模型输出与实际数据的拟合曲线。图3的右半部分为模型输出与实际输出的误差曲线。由图3可明显看出，模型输出以很小的误差趋近机组实际输出，具有很高的拟合精度。

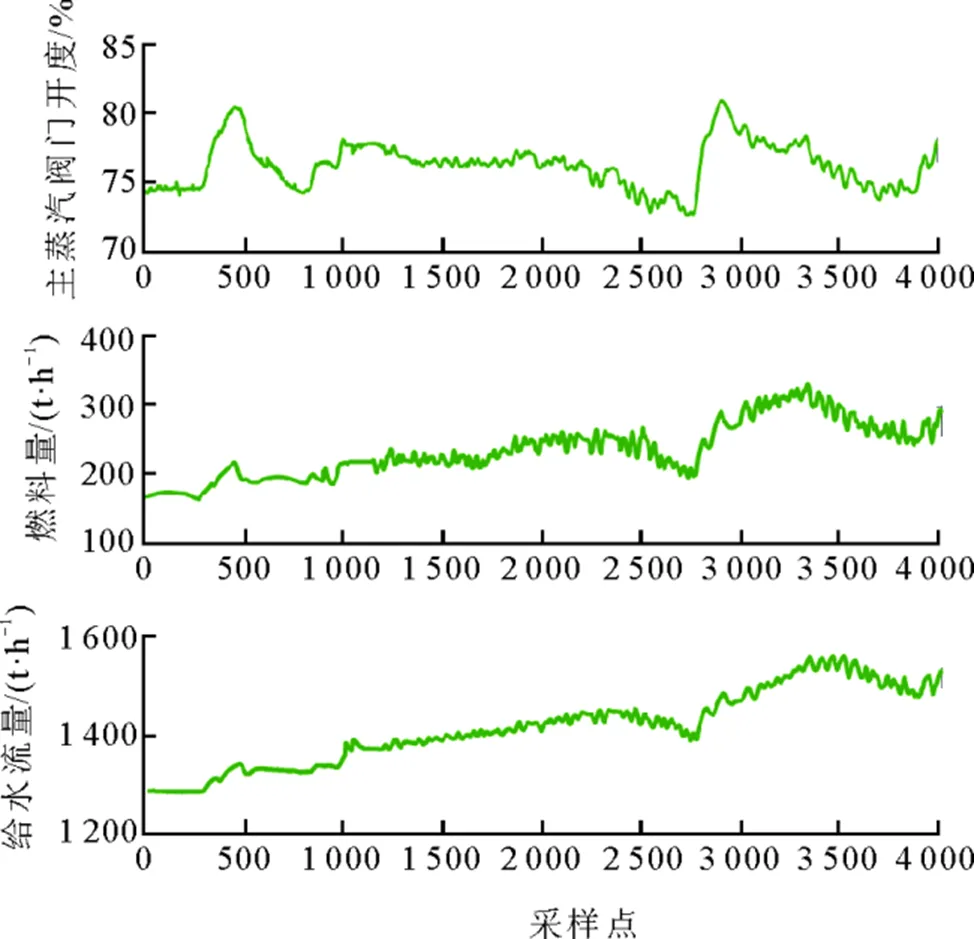
图2 辨识所用输入数据

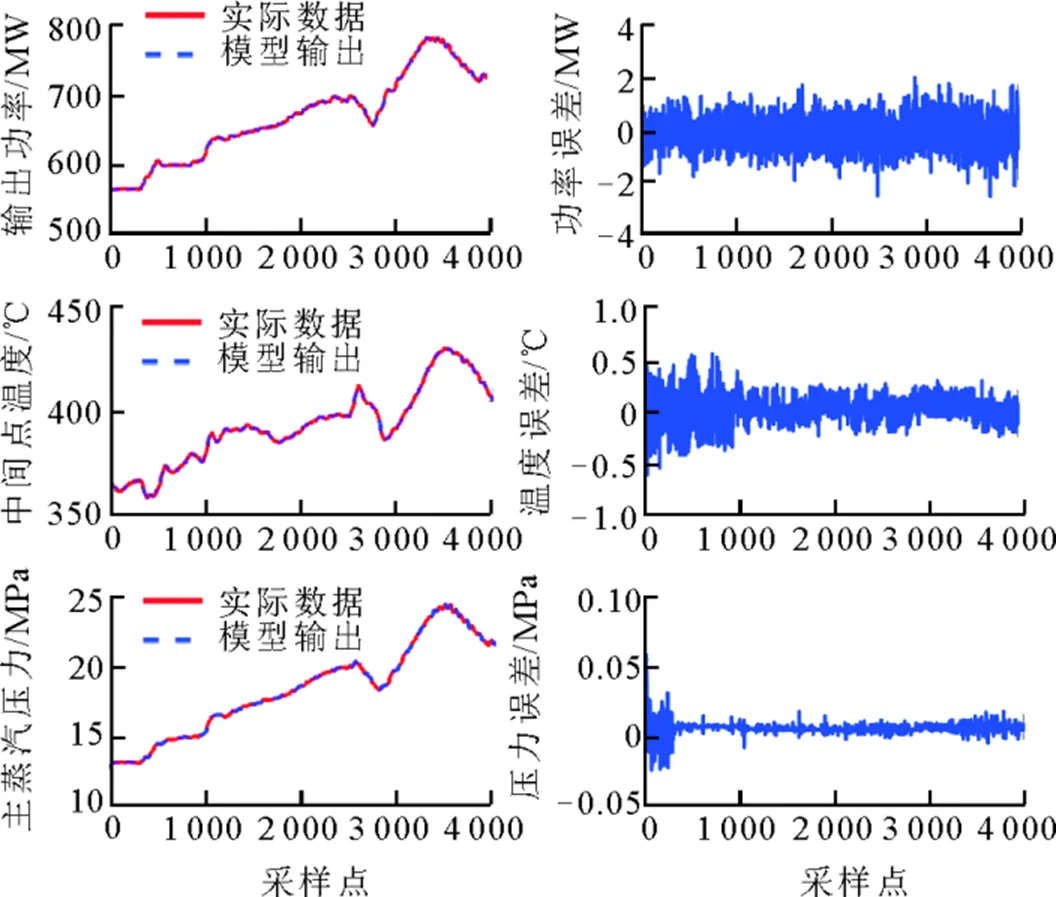
图3 模型输出与实际运行数据的拟合和误差曲线

为进一步证明提出算法在建模过程中的快速性和精确性，在保持结论部分辨识采用指数加权最小二乘算法的前提下，分别将其与基于熵聚类[8]PSO[14]聚类和ABC[21]聚类的T-S辨识算法进行对比，并引入建模时间m和模型输出均方根误差RMSE这2个评价指标，不同建模方法性能指标对比结果见表2。由表2可见，与基于熵聚类、PSO聚类和ABC聚类的T-S辨识算法相比，本文提出的基于QABC聚类的T-S模糊辨识无论是从建模时间还是所得模型精度上都明显优于其他算法，表现出良好性能。

表2 不同建模方法性能指标对比结果

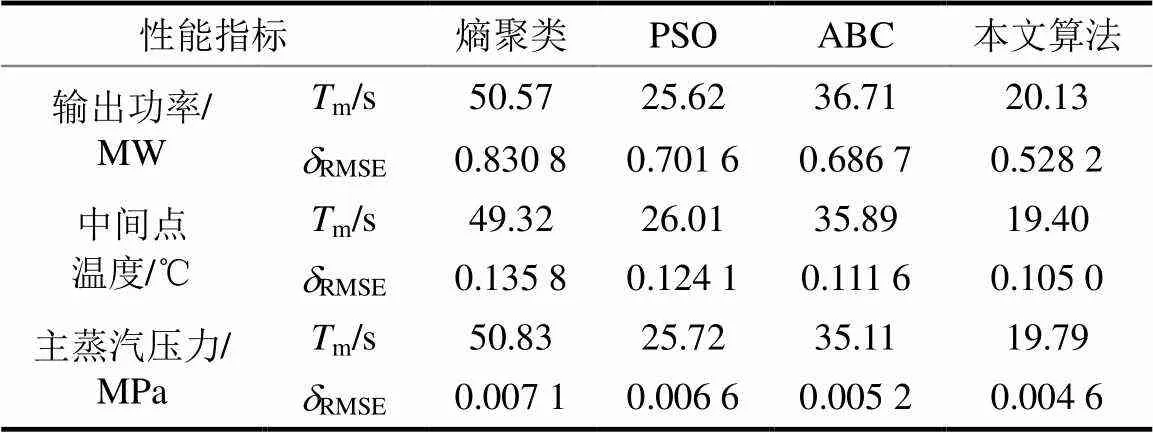
Tab.2 The performance index comparison between different modeling methods

考虑到辨识所得模型在大范围工况的通用性以及变工况下的适应性，将模型输入在另外几组不同工况下的数据间进行切换，观察模型输出与机组实际数据的拟合情况。具体做法是，分别选取3组在60%，80%和100%工况附近的数据集，每组数据集由1 500个采样数据对组成。开始仿真后，先输入80%工况点附近的数据对，到1 500个采样点后切换为100%工况点附近的数据进行输入，再经过 1 500个采样点后输入60%工况点附近的数据对，输入数据如图4所示。

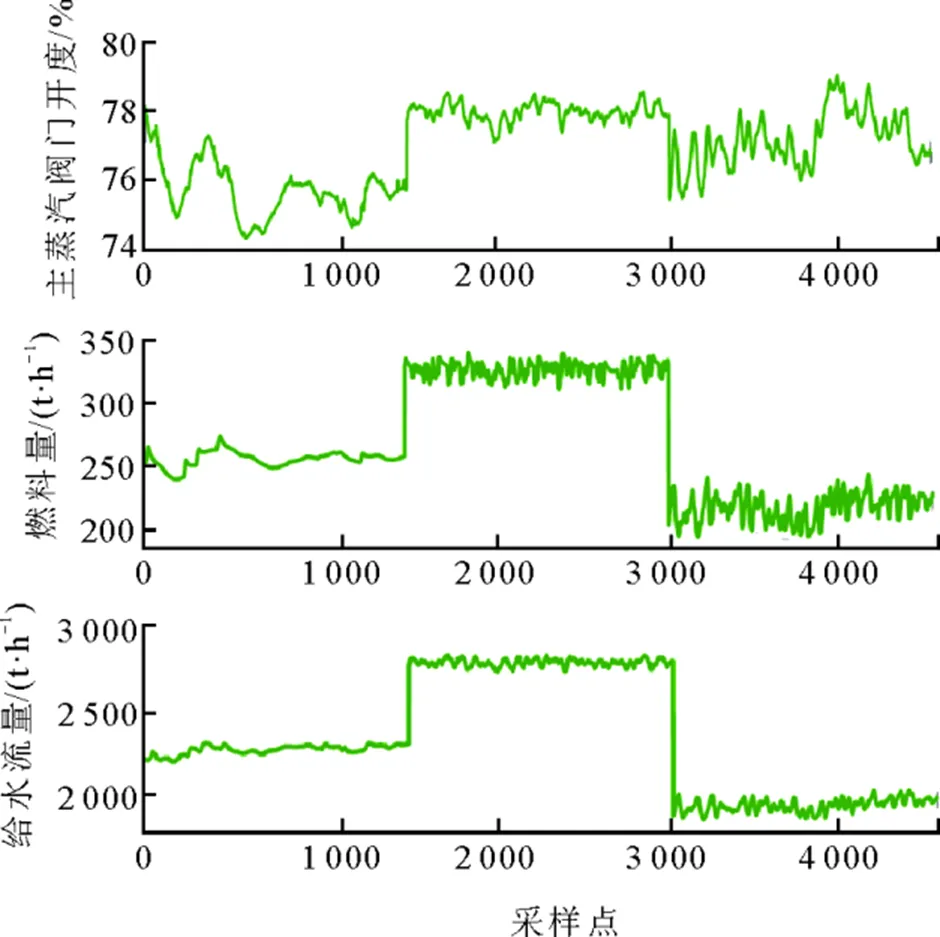
图4 模型通用性测试部分输入数据

由于实际发电过程中工况点变化是一个缓慢的过程，几乎不存在上述突变，所以为保证工况点切换时刻的机组安全稳定运行，令当前切换时刻的模型输出与前一时刻保持一致，在切换的下一时刻再输出由新工况输入数据得到的输出。经过上述工况点切换仿真实验后，最终得到模型输出与实际数据的拟合和误差曲线如图5所示。由图5可以看出，在系统进行大范围变工况时，本文提出方法辨识所得模型输出依然能高精度拟合机组实际输出，表现出极大的通用性和适用性，再次证明了其性能的优越性。

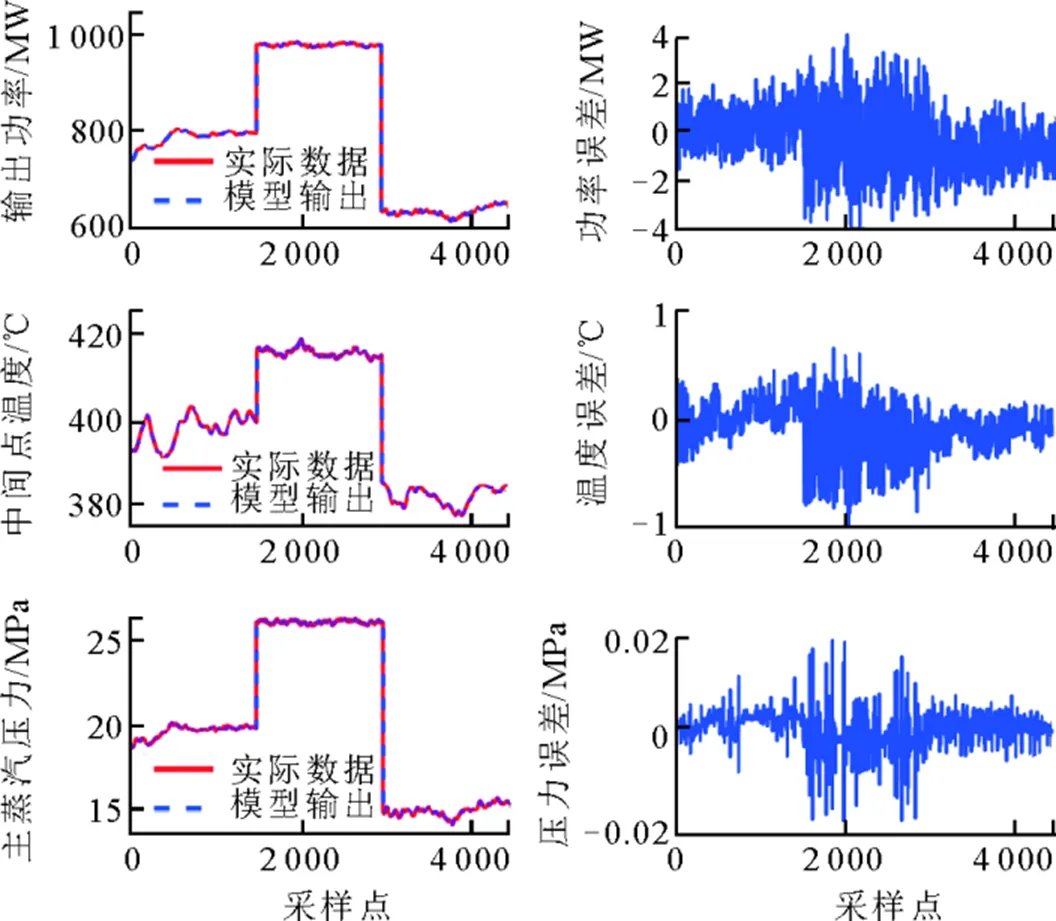
图5 通用性测试中模型输出与实际数据的拟合和误差曲线

4 结 语

本文在综合考虑模型辨识过程快速性和精确性的基础上，提出了一种基于QABC聚类的新型T-S模糊辨识算法，该算法不仅能在不经过人为设定的情况下自动生成聚类中心和聚类半径，还大大提高了模型辨识的速度。仿真实验结果表明，辨识所得模型不仅在特定工况点具有较高精度，在机组大范围变工况下依然保持显著优势。

［1］ 刘吉臻, 王庆华, 房方, 等. 数据驱动下的智能发电系统应用架构及关键技术[J]. 中国电机工程学报, 2019, 39(12): 3578-3587.

LIU Jizhen, WANG Qinghua, FANG Fang, et al. Data-driven-based application architecture and technologies of smart power generation[J]. Proceedings of the CSEE, 2019, 39(12): 3578-3587.

［2］ 刘吉臻. 智能发电: 第四次工业革命的大趋势[N]. 中国能源报, 2016-07-25.

LIU Jizhen. Smart generation: the general trend of the fourth industrial revolution[N]. China Energy News, 2016-07-25.

［3］ 刘吉臻, 胡勇, 曾德良, 等. 智能发电厂的架构及特征[J]. 中国电机工程学报, 2017, 37(22): 6463-6470.

LIU Jizhen, HU Yong, ZENG Deliang, et al. Architecture and feature of smart power generation[J]. Proceedings of the CSEE, 2017, 37(22): 6463-6470.

［4］高海东, 高林, 樊皓亮, 等. 火电机组实用智能优化控制技术[J]. 热力发电, 2017, 46(12): 1-5.

GAO Haidong, GAO Lin, FAN Haoliang, et al. Discussions on practical intelligent optimization control technologies for thermal power units[J]. Thermal Power Generation, 2017, 46(12): 1-5.

［5］ HOU G L, DU H, YANG Y, et al. Coordinated control system modelling of ultra-supercritical unit based on a new T-S fuzzy structure[J]. ISA Transactions, 2018, 74: 120-133.

［6］ ZHU X B, WITOLD P, LI Z W. A Design of granular Takagi-Sugeno fuzzy model through the synergy of fuzzy subspace clustering and optimal allocation of information granularity[J]. IEEE Transactions on Fuzzy Systems, 2018, 26(5): 2499-2509.

［7］ WU X, SHEN J, LI Y, et al. data-driving modeling and predictive control for boiler-turbine unit using fuzzy clustering and subspace methods[J]. ISA Transactions, 2014, 53: 699-708.

［8］ HOU G L, YANG Y, JIANG Z, et al. A new approach of modeling an ultra-super-critical power plant for performance improvement[J]. Energies, 2016, 9(5): 310.

［9］ 赵明, 王培红, 梁俊宇, 等. 基于加权模糊C-均值聚类的锅炉运行参数基准值建模[J]. 热力发电, 2019, 48(1): 12-17.

ZHAO Ming, WANG Peihong, LIANG Junyu, et al. Modeling of reference value of boiler operating parameters based on weighted fuzzy C-means clustering algorithm[J]. Thermal Power Generation, 2019, 48(1): 12-17.

［10］ 盛万兴, 季宇, 吴鸣, 等. 基于改进模糊 C 均值聚类算法的区域集中式光伏发电系统动态分群建模[J]. 电网技术, 2017, 41(10): 3284-3291.

SHENG Wanxing, JI Yu, WU Ming, et al. Dynamic clustering modeling of regional centralized photovoltaic power plant based on improved fuzzy C-means clustering algorithm[J]. Power System Technology, 2017, 41(10): 3284-3291.

［11］ HUSSAIN S F, HARIS M. A-means based co-clustering (CC) algorithm for sparse, high dimensional data[J]. Expert Systems with Applications, 2019, 118: 20-34.

［12］ TANG T L, CHEN SY, ZHAO M, et al. Very large-scale data classification based on-means clustering and multi-kernel SVM[J]. Soft Computing, 2019, 23: 3793-3801.

［13］ ADANEZ J M, AL-HADITHI B M, JIMENEZ A. Multidimensional membership functions in T–S fuzzy models for modelling and identification of nonlinear multivariable systems using genetic algorithms[J]. Applied Soft Computing Journal, 2019, 75: 607-615.

［14］ ZHAO L, QIAN F, YANG Y, et al. Automatically extracting T-S fuzzy models using cooperative random learning particle swarm optimization[J]. Applied Soft Computing, 2010, 10(3): 938-944.

［15］ 曹满婷, 刘楠, 李晓苗. 基于猫群算法的模糊建模[J]. 控制工程, 2018, 25(6): 1127-1133.

CAO Manting, LIU Nan, LI Xiaomiao. A fuzzy modeling method based on cat swarm optimization[J]. Control Engineering of China, 2018, 25(6): 1127-1133.

［16］ HOU G L, GONG L J, HUANG C Z, et al. Novel fuzzy modeling and energy-saving predictive control of coordinated control system in 1 000 MW ultra-supercritical unit[J]. ISA Transactions, 2019, 86: 48-61.

［17］ WU X, SHEN J, LI Y, LEE K Y. Fuzzy modeling and predictive control of superheater steam temperature for power plant[J]. ISA Transactions, 2015, 56: 241-251.

［18］ LI L Q, WANG X L, XIE W X, et al. A novel recursive T-S fuzzy semantic modeling approach for discrete state-space systems[J]. Neurocomputing, 2019, 340: 222-232.

［19］ 席嫣娜, 王印松. 一种基于自适应反演算法的火电单元机组协调控制策略[J]. 中国电机工程学报, 2018, 38(7): 2070-2081.

XI Yanna, WANG Yinsong. A coordinated control strategy for thermal power generation units based on the adaptive backstepping method[J]. Proceedings of the CSEE, 2018, 38(7): 2070-2081.

［20］ HABBI H, BOUDOUAOUI Y, KARABOGA D, et al. Self-generated fuzzy systems design using artificial bee colony optimization[J]. Information Sciences, 2015, 295: 145-159.

［21］ 夏卓群, 欧慧, 李平, 等. 基于改进流形距离和人工蜂群的二阶段聚类算法[J]. 控制与决策, 2016, 31(3): 411-416.

XIA Zhuoqun, OU Hui, LI Ping, et al. Two-phase clustering algorithm based on the improved manifold distanceand the artificial bee colony algorithm[J]. Control and Decision, 2016, 31(3): 411-416.

Application of T-S fuzzy modeling based on quantum bee colony clustering in smart power generation operation control

HOU Guolian, GONG Linjuan

(School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China)

Establishing an accurate model for power plant under working conditions with wide range is the most fundamental and critical part of smart power generation operation control. In order to improve the rapidity of the modeling process and the accuracy and versatility of the identified model, a new T-S fuzzy modeling method based on quantum bee colony clustering is proposed in this paper. Firstly, the quantum bee colony is presented as clustering algorithm for the premise part identification. Not only the clustering speed is improved through the introduction of quantum concepts, but also the subjectivity caused by artificially set clustering number is eliminated through the decision constants and data space constraint. Then, the exponential weighted least squares method is used in consequent part identification to ensure the simplicity and accuracy of the local model. Finally, taking the modeling of the coordinated control system in ultra-supercritical power plant as an example, the application of the proposed algorithm in the modeling of power plant in the intelligent power generation operation control system is discussed. The simulation results illustrate that, this proposed algorithm not only ensures the rapidity of the modeling process, but also makes the identified model maintain high precision and show well superior versatility and adaptability.

smart power generation, operation control, quantum bee colony clustering, T-S fuzzy modeling, coordinated control system, wide range varying working conditions, model identification, ultra-supercritical power unit

TM61；TP273

A

10.19666/j.rlfd.201907127

2019-07-03

中央高校基本科研业务费专项资金项目(2019JG004)

Supported by：Fundamental Research Funds for the Central Universities (2019JG004)

侯国莲(1966—)，女，博士，教授，主要研究方向为发电过程建模与控制，hgl@ncepu.edu.cn。

侯国莲, 弓林娟. 基于量子蜂群聚类的T-S模糊建模在智能发电运行控制中应用[J]. 热力发电, 2019, 48(9): 108-114. HOU Guolian, GONG Linjuan. Application of T-S fuzzy modeling based on quantum bee colony clustering in smart power generation operation control[J]. Thermal Power Generation, 2019, 48(9): 108-114.

（责任编辑 马昕红）