基于CFD的文丘里施肥器收缩与扩散段结构优化
2019-09-27王秋良王振华吴文勇谢东辉
王秋良,王振华,吴文勇,谢东辉
(1.石河子大学水利建筑工程学院,新疆 石河子 832000;2.中国水利水电科学研究院,北京 100048)
“十二五期间”我国节水灌溉面积0.3106 亿hm2,高效节水灌溉工程面积达到0.1793 亿hm2,微灌面积526.3 万hm2,园地灌溉面积0.024 7 亿hm2,而文丘里施肥器因维修简单,价格低廉,生产容易,实用性强被广泛应用于微灌技术中[1,2]。目前,国内对文丘里施肥器的研究主要包括结构参数优化、空化作用、新技术与水肥调控一体化、理论模型简化4个方面。结构参数优化方面,运用CFD软件计算与试验研究揭示了喉管进出口直径之比与进出口直径、收缩与扩散角、收缩与扩散段长度等参数对吸肥量、压差、负压、吸肥浓度、临界流量与压力、水头损失的相关关系,验证了模拟的可靠性,提出了适应的公式,开发了新型的施肥器[3-12];空化作用研究方面,结合高速摄像技术拍摄,结合实验与数值模拟,分析了施肥器内部流动,得到了发生空化作用时施肥器的临界压力,阐述了吸肥性能的变化规律[13-18];新技术与水肥调控一体化研究方面,以文丘里施肥器为核心部件,运用3T扫描技术、3D打印技术,计算机技术,控制施肥器的性能与结构相关参数,开展了水肥一体化实验研究,综合评估施肥系统 稳定与可靠性[19-23,29];理论模型简化方面,结合数学统计软件对施肥器理论公式进行简化,阐明了相关要素对吸肥性能的影响[1,24]。这些研究都有较好的进展,尤以CFD为基础研究新型施肥器成为热点,但是对于同时改变收缩段与扩散段组合形式对吸肥性能影响鲜少提到,本文运用CFD软件对比文献[19,29,30]实验结果喉管进出口直径之比λ=1.27,对收缩段与扩散段组合形式进行结构优化,以期提出新型文丘里施肥器结构模型,为该种类型施肥器研发提供设计方法与理论基础。
1 材料与方法
1.1 文丘里施肥器相关结构参数
本文基于7种不同结构参数ATP型文丘里施肥器流道模型[19,29,30],产品型号如表1所示,另外提出7种不同组合形式的收缩段与扩散段模型。这7种模型喉管进出口直径之比λ相同情况下,收缩段与扩散段不同,收缩段与扩散段分为喇叭口形,流线形。方案a~g依次对应模型一至七。不同模型主要异同为增加喉管前过渡段、喉管过渡段倒圆弧、扩散段出口为流线形4种类型。模型一与模型二的主要差别为扩散段不同;其中模型二与模型三扩散段不同,模型三为流线形扩散段;模型三与模型四主要差别为收缩段不同,模型四喉管前端与收缩段为折角连接;模型四与模型五收缩段不同,模型四收缩段靠近喉管处倒圆角过渡;模型五与模型六收缩段不同,模型六收缩段为流线形;模型六与模型七收缩段不同,收缩段都为流线形,但模型六过渡段倒了圆角。给出其中7种施肥器内部腔体对称剖面如图1所示,引用无量纲数λ,为喉管出口直径与进口直径比值(d2/d1)。

表1 14种文丘里施肥器基本结构参数
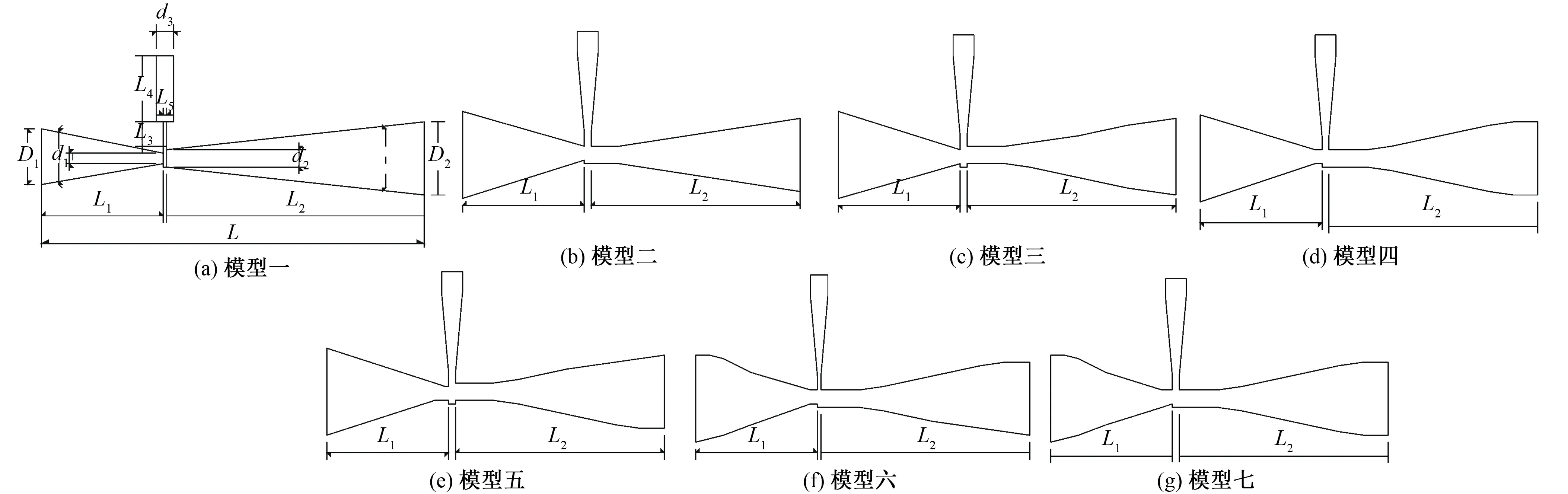
图1 文丘里施肥器流道模型
图1(a)中,文丘里管由渐缩管段,喉管段和渐扩管段3部分组成。D1为进口直径,mm;D2为出口直径,mm;L为主管段长度,mm;L1为渐缩管长度,mm;L2为扩散段长度,mm;α为收缩角,°;β为扩散角,°;L3为吸肥管颈部长度,mm;L4为吸肥管进口长度,mm;L5为喉管长度,mm;d1为喉管进口直径,mm;d2为喉管出口直径,mm;d3为吸肥口直径,mm;施肥器内部流道在喉管处发生突变,流速急剧增大,造成了喉管部压力发生大幅度减少,真空度增大,肥液通过吸肥口被吸入。
1.2 施肥器建模
1.2.1 建模与网格划分
根据原始模型图1(a),简化吸肥段,并用三维建模软件solidworks2016对上述14种不同结构模型进行建模;运用ICEM对前处理的三维模型进行网格划分;采用非结构网格,在网格从110万到150万增加的过程中发现随着网格数的增加,对吸肥量计算结果并没有太大的影响,因而设置全局网格尺寸为0.8,为了得到喉管进出口改变情况下施肥器内部流态的分布情况,对喉管部分进行网格加密处理,喉管部分的局部网格尺寸为0.2,吸肥管段为0.4,其他部分网格尺寸为0.8,其中7种不同模型网格质量都大于0.4,满足工程计算要求,三维模型、网格划分和切面分割如图2所示。

图2 三维结构模型、边界条件设置、切面分割
1.2.2 吸肥器数学模型
文丘里施肥器内部主要为水和肥液,近似认为过流流体不可压缩液体,本文主要研究常温下流场分布情况。严海军等利用CFD模拟对文丘里施肥器进行计算,比较了标准k-ε、RNG,Realizable 3种湍流模型的计算精度,发现应用标准k-ε模型计算最稳定,除了近壁面都为湍流[25],因而采用k-ε模型对本文模型进行计算,方程模型如下[26]:
连续性方程为:
(1)
N-S方程表示控制方程为:
(2)
(3)
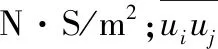
k-ε双方程模型:
(4)
(5)
(6)
式中:Gk为由于平均速度梯度引起的湍动能κ产生项;Gb为由于浮力引起湍动能变化产生项;YM为可压湍流中脉动扩张的贡献;C1ε,C2ε,C3ε均为经验常数;δk,δε分别为湍动能k与耗散率ε对应的普朗特数;Sk和Sε均为用户定义的源项。
本文中模型相关参数的取值为:C1ε=1.44,C2ε=1.92,Cμ=0.09,δk=1.0、δε=1.3、C3ε=0,Gb=0,YM=0,Sk=0,Sδ=0,Cμ为常量,κ为湍流动能,ε为湍动能耗散率,μt为湍流黏度。
1.2.3 边界条件设置
(1)进口边界条件:将进水端设置为压力进口,给定压力值依次为0.05、0.10、0.15、0.20、0.25、0.30、0.35 MPa进行计算。
(2)出口边界条件:将出水口设置为压力出口,给定压力为0。
(3)吸肥口边界条件:将吸肥口设置压力自由液面,与大气相通。
(4)其他边界条件:其余所有壁面都采用无滑移边界条件。
(5)计算残差收敛精度设置为10-4。
2 结果与分析
2.1 试验与模拟验证
首先,对原有的7种ATP施肥器进行模拟与试验对照得到最佳喉管进出口比值λ,把入口流量作为主参数,通过下面公式计算文丘里施肥器的吸肥性能[5]。
(7)
式中:η为吸肥效率,用于反应文丘里施肥器的综合吸肥性能,%;q为吸肥量;Q1为进口流量,L/h;Q2为出口流量,L/h;ΔP、P1、P2分别为文丘里施肥器进出口压差、进口压力、出口压力,MPa;γ为肥液浓度,直观反应施肥器的性能优劣,%;δ为肥液比,直观反应施肥器的吸肥能力,%。
对原有7种模型的施肥器进行建模计算与文献[19,29,30]对比分析,得到η~Q1曲线如图3所示。
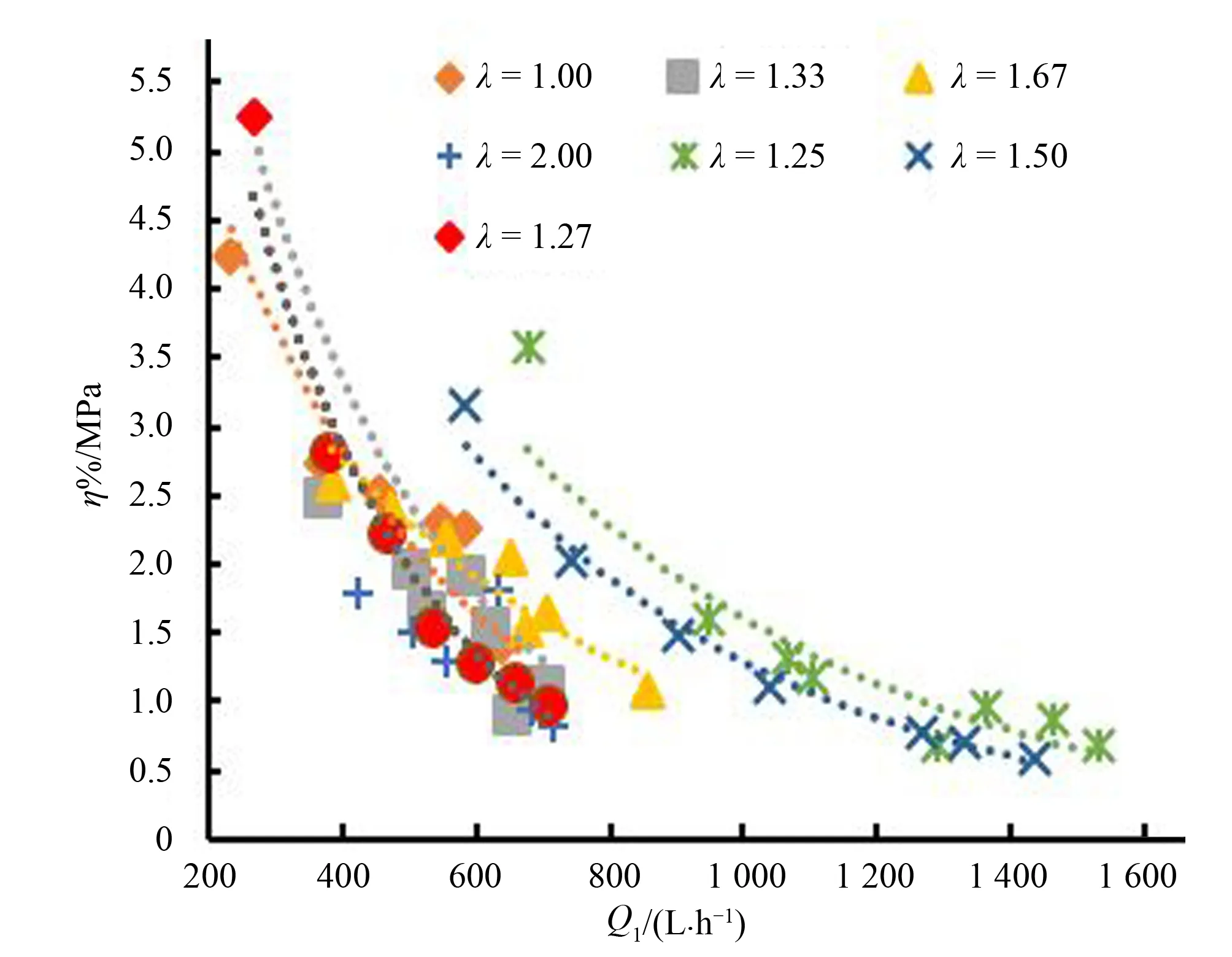
图3 η~Q1关系曲线
由图3可知:吸肥效率随着进口流量的增大而减小,施肥器进口流量越大,吸肥效率减小的速度越缓,与实验结果得到的结论相同,得到λ误差仅为8.6%[19,29,30];另外由表2可知,
表2 6种原始进口流量模拟与实验误差

%
以进口流量为主参数,得到模拟与实验结果表明两者误差在可接受的范围之内,可认为计算结果正确,模拟具有较高的可靠性。为了进一步研究该λ情况下,得到最优组合形式的收缩与扩散段结构,探讨不同文丘里施肥器收缩段与扩散段组合形式对吸肥性能的影响,对提出7种不同收缩与扩散段结构模型计算结果进行分析。
2.2 收缩与扩散段对吸肥性能的影响
依次取λ为1.00、1.25、1.33、1.50、1.67、2.00时计算结果与文献[19,29,30]实验进行对比得到λ=1.27情况下,对提出的7种结构模型(见图2),研究收缩段与扩散段相关参数对吸肥性能的影响,并结合公式(1)~(7)进行分析,选择最佳收缩段与扩散段结构,如表3所示。
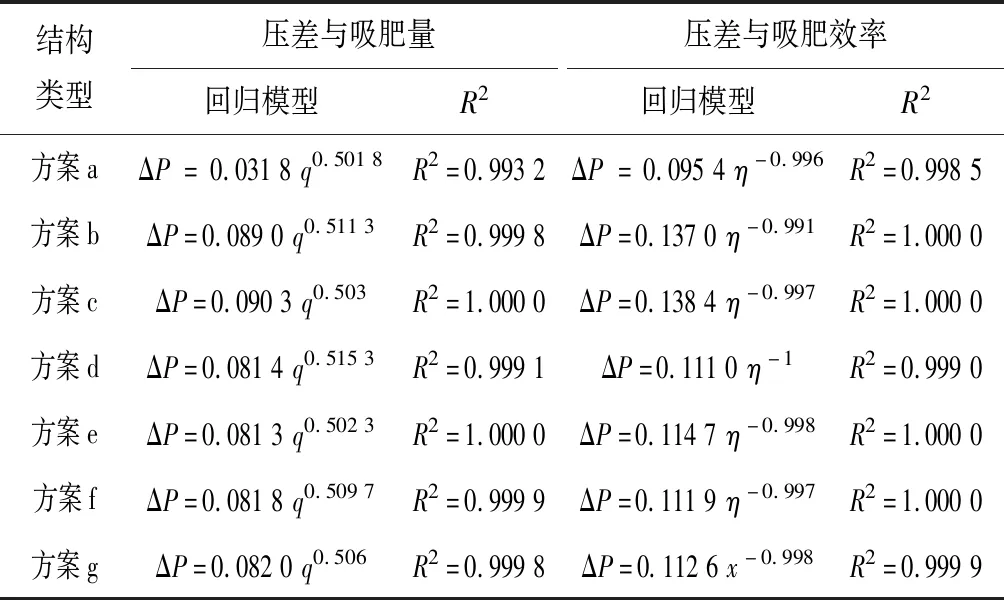
表3 压差与吸肥量、吸肥效率回归公式
当λ=1.27条件下,根据图4曲线与表3可得,吸肥量与压差呈幂函数的趋势变化,吸肥量随着压差的增加而增大,但是增大的越来越缓慢,压差与吸肥效率呈现指数趋势递减,递减趋势随着压差增大而减少,这是因为喉部负压达到了极值,吸肥量不再增加。在相同的压差情况下:对于吸肥性能而言,方案b、c明显比方案a、d、e、f、g 5种方案有较大提升。其中,方案c吸肥效率最高,最大达到了2.8%,与同等条件下的实验进行对比,即λ取1.00、1.25、1.33、1.50、1.67、2.00时,在不同的压力情况下,吸肥量均最大,吸肥效率最大提高了5.6%、9.0%、45%、42%、17%、12%;其次,方案c吸肥浓度与肥液比分布最为均匀,吸肥浓度达到了12.2%,肥液比最大达到了13.7%,不同工况的综合适应性能力最强;方案g最差,与其他5种结构对比表明喉管进出口直径扩大对施肥器性能影响显著;在方案c、d、e、f 4种不同的方案下,扩散段相同,不同的收缩段对施肥器吸肥效率影响很大,在收缩段增加直线过渡段会增加沿程阻力损失,影响喉部压力分布,耗散主管中流体主流能量,对吸肥有一定的影响;方案e与d和方案f与g两组方案对比都表明在喉管进口处附近采用倒圆角结构对施肥器吸肥性能有较大改善,这是由于局部采用圆弧过渡段能够很大程度上的减少局部水头损失,故设计过程中可以考虑采用圆弧倒角结构;在相同的收缩段的情况下,方案b与c对比表明扩散段采用流线型结构对施肥器流场分布有很大影响从而体现于吸肥性能有差异,故扩散段宜采用流线型出口;在相同的扩散段的情况下,对方案d与g两种方案进行分析发现,流线型收缩段结构比喇叭口收缩段吸肥量、吸肥效率、吸肥浓度、肥液比都小,表明方案d收缩段结构更为优越,故宜采用喇叭口收缩段。另外,对方案c与λ取1.00、1.25、1.33、1.50、1.67、2.00实验吸肥量进行对比由表4可知:该种方案施肥器的吸肥量都比其他6种实验模型大,并且比同类产品吸肥量最大增加80%,综述所述可以判断方案c结构组合形式最优。
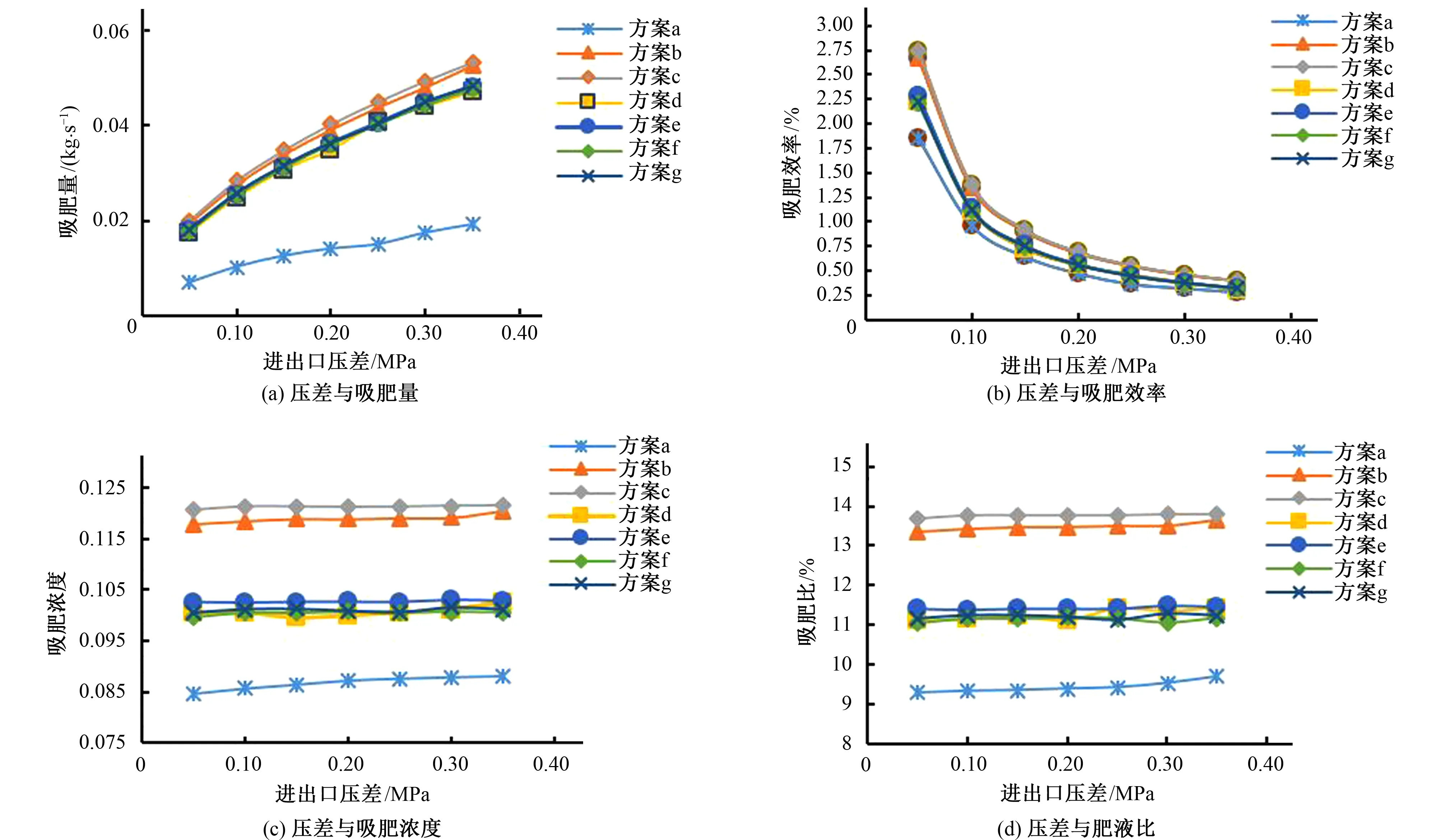
图4 不同方案吸肥性能参数关系对比
表4 方案c吸肥量与6种实验模型对比kg/s

类型进出口压差/MPa0.05000.10000.15000.20000.25000.30000.3500方案c0.02000.02840.03480.04020.04500.04930.0533ATP3-30.01970.02890.03140.03940.04440.04390.0450ATP3-40.01640.02640.03470.03720.04330.04670.0511ATP3-50.01110.02330.03560.04250.04690.04810.0517ATP3-60.01170.02670.03280.03720.04500.04880.0512ATP4-50.01820.03140.03420.03990.04160.04790.0527ATP4-60.01980.02800.03430.03960.04400.04750.4970
2.3 不同收缩与扩散段对流场分布的影响
为了研究7种不同模型收缩与扩散段对流场的分布影响:对压力随施肥器长度方向的变化、速度场以及流线分布情况进行讨论。以0.05 MPa为例,对模型进行长度方向上的切割,切分间距为5 mm得到不同断面的压力值,平均湍动能值,另外对施肥器进行对称平面的切割如图2(c)所示,分析速度与流线在流场分布。
2.3.1 对压力分布的影响
如图5所示,该系列施肥器,以进口处断面平均压力作为参考点,随着长度的增加压力先减少后增大,靠近收缩段尾端接近喉管进口处时变化最为剧烈,最大压力出现在喉管出口处右侧,这是由于在肥液管中肥液与主流混合后,该处内部流态复杂能量转化迅速,同时也会产生较大局部水头损失。远离喉管出口段X=0.2 L处以后压力分布慢慢恢复均匀稳定状态,这也说明压力变化幅度大的区间为[-0.1 L,0.2 L],产生负压的区间为[0,0.2 L]增大这一负压区将对吸肥有促进作用;其中,施肥器主管中流体在收缩段时,未到达喉管进口处之前,方案c压力均匀分布段最长,在到喉管进口处前的区间之内变化最小,表明该结构方案对压力变化具有较高适应性;在X=0.05 L处,即喉管出口处向右移的位置,方案c的压力最小,真空度最大,数值约为0.025 MPa,小于真空度0.09 MPa[7],不会产生空化现象,表明方案c在喉管处产生负压最大对吸肥最为有利。

图5 断面平均压力随长度方向变化情况
2.3.2 对速度分布的影响
根据图6可知:同种工况下,在X方向,不同收缩段与扩散段对速度分布有很大的影响,方案a~g速度从主流的进口处到出口处,速度呈现先增大后减少的趋势,最大速度出现在主管与吸肥管交叉位置处正下方附近。从图6施肥器吸肥管与主管交叉处速度依次为:10.32、10.78、12.00、11.00、11.32、11.76、11.37 m/s。方案a在收缩段与扩散段,对于其他的6种而言速度分布最不均匀,在喉管附近速度改变梯度大,这是由于水流从吸肥管进入喉管中流动方向发生改变,与收缩段来流水流发生碰撞,能量迅速发生转化。交叉处由于水流的剪切与横向环流作用,使进入直管的水流出现较为明显的流速梯度,在吸肥管靠近主管侧壁容易产生低速回流区,造成产生旋涡、耗散了主流的能量、降低了吸肥效率、影响了施肥器的工作性能[25,27,28],扩散段较大的负压区向下延伸持续影响后面的速度分布。 方案c对比其他的6种方案喉管处所对应的速度最大,压力最小,负压最大,距离吸肥口进口处的速度也最大,表明吸肥量最大,吸肥性能最好,也证实了方案c为最优方案。
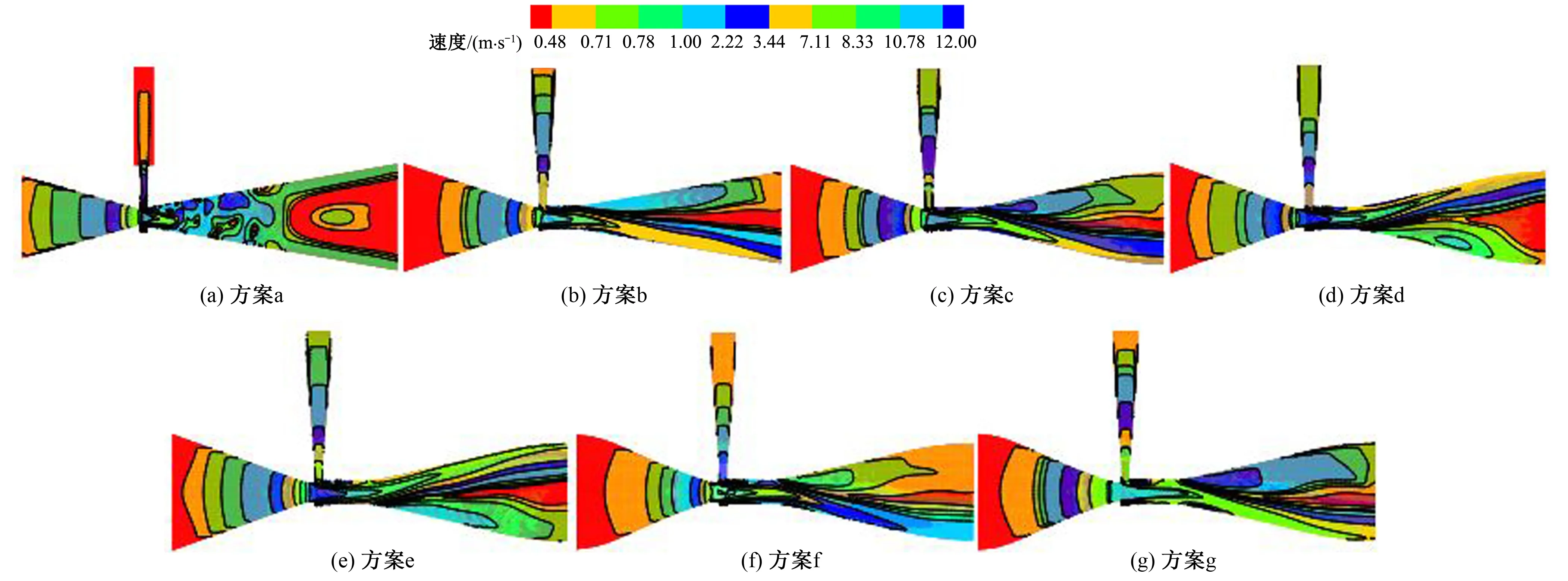
图6 速度云图
2.3.3 对流线与湍动能分布的影响
根据图7可得:后6种方案流线分布对比方案a每种都有很大改善,方案b~g流线分布都比较均匀,只是在主流的出口处产生了旋涡区,避免了在喉管附近产生旋涡区,耗散该区域的主流的能量,提高了吸肥性能,其中方案b、c、e、f、g这5种方案旋涡区的中心都比方案d要好,因为旋涡区距离扩散段进口处越远,可以尽量避免旋涡区对扩散段较长区间流场的干扰,尽可能减少能量损失。方案b与d、方案c与e两组进行对比发现收缩段增加过渡段一定程度上会影响主流区域范围的变化,可能是沿程损失造成的。为了进一步的分析得到方案b、c、d、e、f、g这6种方案最优流线分布,提取X=0.05 L处平均湍动能k,得到方案b~f的k值依次为0.381、0.325、0.795、0.626、0.355、0.344 m2/s2,表明c方案对应的湍动能最小,局部水头损失最小,可以选择方案c流线分布为最优方案。

图7 流线图
3 结 语
(1)本文以入口流量为主参数,模拟计算实验的7种ATP型文丘里施肥器在不同工况下的工作状态,得到入口流量Q1与喉管最佳进出口比λ的值对比实验分析,发现两者误差在可以接受的范围之内,证明了模拟的可靠性。
(2)在最佳喉管进出口比λ=1.27情况下,提出7种不同的结构模型,研究收缩段与扩散段对施肥器吸肥性能的影响,得到压差与吸肥量呈幂函数关系变化,压差越大吸肥量越大,增大趋势越来越缓慢;压差与吸肥效率呈指数关系变化,吸肥效率随着压差增大而减少,压差越大,减少的幅度越小;结合吸肥量q、肥液比δ、肥液浓度γ、吸肥效率η,4个指标得到了一种新型的施肥器结构小收缩角收缩段与流线型扩散段组合,该种方案施肥器比同类ATP产品吸肥量最大增加80%,并且对不同工况适应性最强,吸肥最稳定。
(3)当工况为0.05 MPa时,通过对比分析7种结构流场中的压力,速度,流线,湍动能的分布情况,发现喇叭口收缩段流线型扩散段结构方案喉管附近速度最大、产生的真空度最大、湍动能最小、旋涡区较小、流线分布均匀,进一步证实了喇叭口收缩段与流线型扩散段结构方案比其他6种好。
