混合肥液电导率预测模型构建研究

余 淋，郝祝霞，张京萍，许德华，刘敦一，刘洪滨，束维正，王辛龙

（1.西南大学 资源与环境学院，重庆 400000；2.安徽农业大学 资源与环境学院，安徽 合肥 230036；3.四川大学 化学工程学院，四川 成都 610000；4.中盐安徽红四方肥业股份有限公司，安徽 合肥 230036）

0 引言

水溶性肥料是经水溶解或稀释，用于灌溉施肥、叶面施肥、无土栽培、浸种蘸根等用途的液体或固体肥料［1］，具有配方灵活、营养全面、肥效快、吸收好、功能多、针对性强等突出特点［2-3］。水溶性肥料可以水肥同施，以水带肥，充分发挥水肥协同效应，既能减少施肥用工成本、提高肥料利用率，又能减少环境污染和资源浪费［4］，将成为我国肥料产业的主要发展方向。作物生长过程中对肥料浓度较为敏感，肥料浓度过高会影响作物的水分吸收从而造成叶片水含量降低［5］，岩学斌等［6］研究发现，随着肥液浓度增加，叶片会出现失水卷曲、叶尖发黄甚至整个叶片干枯死亡的症状；肥液浓度过低则会使作物营养不良、生长缓慢，从而导致生物量低［7］。因此，在水溶性肥料施用过程中必须要严格调控肥液浓度，在适宜的浓度范围内，提高肥液浓度能够促进作物生长，从而达到增产、提质的效果［8-9］。许多学者的研究表明肥液电导率（EC）和肥料质量浓度之间存在着显著的正相关关系［10-11］。为了准确调控肥料用量，研究者通常使用电导率来反映肥料浓度［12］。李加念等［13］基于电导电极设计了一种通过测量肥液电导率间接测定肥液浓度的在线检测仪，其平均相对误差为2.77%；赖胜等［14］基于离子电极设计了一种营养液在线检测系统，能够实时检测营养液中的硝酸根、钾离子和钙离子浓度；范丽等［15］基于电磁感应原理设计了一种电导率传感器及其测量系统，相对误差小于1%，满足作物营养液电导率的测量要求。

目前对肥液电导率研究存在以下不足：（1）肥液电导率的研究主要集中在通过测定肥液电导率间接实现肥液浓度检测上，以电导率为因变量的模型构建探究却极少有报道［16］；（2）目前基于电导率的肥液浓度监测只能监测单一种类肥液浓度［17］，在混合肥液的浓度监测中应用较少。因此，笔者基于肥液电导率与质量浓度之间的关系，选用7种水溶性较好的原料（尿素、硫酸钾、氯化钾、磷酸二氢钾、锌工铵、聚磷酸铵、磷酸一铵）两两组合，根据不同作物对高氮、高磷、高钾、平衡型4种水溶性肥料的需求调整配比值筛选出6组混合肥样，分别测定其在不同配比值、总养分质量分数条件下的电导率，通过拟合实验数据构建以混合肥液配比值、总养分质量分数为自变量，电导率为因变量的函数模型，对混合肥液的电导率进行预测，旨在实现水溶性肥料的智能化配制、精细化管理，为水溶性肥料在农业生产中应用和调控提供技术支撑。

1 材料与方法

1.1 实验设计

根据电解质理论可知，溶液导电是由于溶液中离子定向运动，因此，只要影响溶液中离子运动速度以及离子数量的因素都会对溶液的导电能力存在影响［18］。影响离子数量的因素主要是电解质的浓度和电离度，影响离子运动速度的因素主要有离子性质、溶液总浓度、温度和溶剂黏度［19］。选用尿素-氯化钾、尿素-硫酸钾、尿素-磷酸二氢钾、锌工铵-氯化钾、聚磷酸铵-氯化钾、磷酸一铵-氯化钾6种混合肥样进行肥液电导率变化研究。实验主要分为3部分：（1）基于作物对不同养分的需求设置了5种配比值（N与K2O质量比，分别为1∶3、1∶2、1∶1、2∶1、3∶1），以研究配比值对混合肥液电导率的影响；（2）设置5 个总养分质量分数（0.4%、0.6%、0.8%、1.0%、2.0%），以研究总养分质量分数对混合肥液电导率的影响；（3）设置5种配比值（1∶3、1∶2、1∶1、2∶1、3∶1）和5 个总养分质量分数（0.4%、0.6%、0.8%、1.0%、2.0%）的正交实验，以研究配比值和总养分质量分数耦合作用对混合肥液电导率的影响。

1.2 实验原料

尿素（46-0-0），磷酸二氢钾（0-52-34），中盐安徽红四方肥业股份有限公司；磷酸一铵（12-61-0），湖北世龙化工有限公司；氯化钾（0-0-62），华垦国际贸易有限公司；硫酸钾（0-0-52），青岛碱业钾肥科技有限公司；锌工铵（11-54-0+微量元素），嘉施利化肥有限公司；聚磷酸铵（18-58-0），贵州川恒化工股份有限公司；去离子水。

1.3 实验方法

1.3.1 溶液配制

按表1所示的混合肥样配方准确称量尿素、氯化钾、硫酸钾、磷酸二氢钾、锌工铵、聚磷酸铵、磷酸一铵，加填充物分别配制6 种混合肥样品各100 g。用电子天平准确称量一定量的混合肥样品于100 mL 烧杯中，加入适量去离子水，搅拌至肥料完全溶解后转移至100 mL 容量瓶中，用适量去离子水洗涤烧杯2～3 次，移入容量瓶内。待容量瓶内溶液稳定至20 ℃后，定容，摇匀待用。

表1 混合肥样配方

1.3.2 电导率测定

将电极提前预热并浸入待测溶液中，调节恒温水浴锅的温度（配合高精度温度计使用），待温度恒定至30 ℃后，读取溶液的电导率。

1.4 模型构建与检验

基于总养分质量分数、配比值及总养分质量分数和配比值耦合作用对混合肥液电导率影响的实验数据，用Origin 2022 软件拟合以总养分质量分数、配比值为自变量的二元函数方程。在关系曲线拟合时，为了定量描述拟合曲线与原始数据之间的误差大小，引入拟合方程决定系数（R2）作为衡量曲线拟合优劣程度的定量指标，并通过比较R2来确定最优混合肥液电导率预测模型［20］。配制一系列不同总养分质量分数、不同配比值的混合肥液，分别测定其在30 ℃时的电导率，利用测定结果对建立的预测模型进行检验，通过计算预测值与实测值之间的平均相对误差（MRE）和相对均方根误差（RRMSE）来检验预测模型的精确度，通过计算偏差（θ）来检验预测模型的准确度［21］。

式中，n为样本数，Pi为混合肥液电导率预测值，Oi为混合肥液电导率实测值，Oi为所有样本电导率实测值的平均值。

2 结果与分析

2.1 溶液电导率影响因素分析

2.1.1 配比值对混合肥液电导率的影响

6 组混合肥液的导电能力随着配比值的增大而减小（见图1）。混合肥液的电导率与溶液中离子的物质的量浓度和离子大小有关［22］。在组合1至3中，随着配比值增大，尿素在混合肥液中所占的比例升高，混合肥液中的总离子浓度降低，进而导致参与导电的离子浓度降低。在组合4 至6 中，随着配比值增大，混合肥液中半径大的离子如HPO42-所占比例增加，而离子半径越大在溶液中运动速率就会越慢。

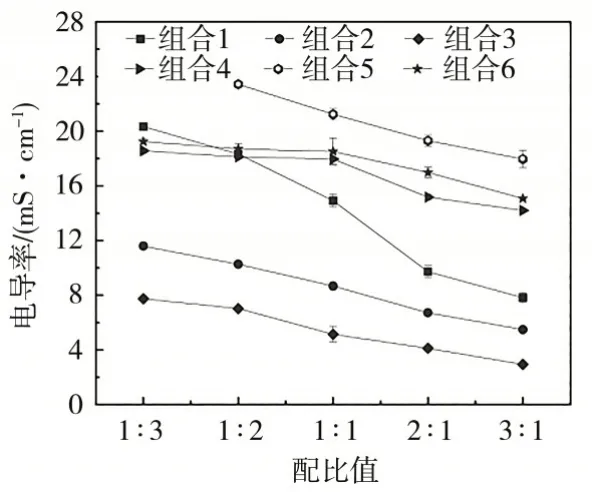
图1 混合肥液电导率随配比值的变化

2.1.2 总养分质量分数对混合肥液电导率的影响

6 组混合肥液的电导率都随着总养分质量分数升高而增大（见图2），这说明总养分质量分数升高有助于提升混合肥液的导电能力。

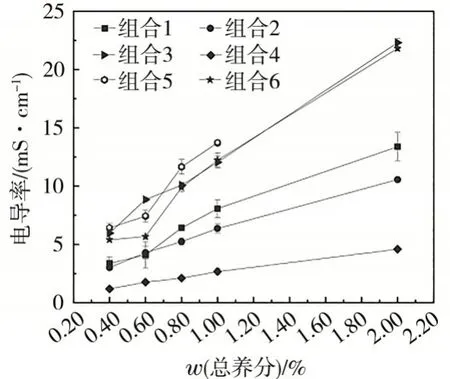
图2 混合肥液电导率随总养分质量分数的变化

2.1.3 总养分质量分数和配比值耦合作用对混合肥液电导率的影响

为了探究总养分质量分数和配比值耦合对混合肥液导电能力的影响，在30 ℃时，测定了不同配比值（1 ∶3、1 ∶2、1 ∶1、2 ∶1、3 ∶1）和不同总养分质量分数（0.4%、0.6%、0.8%、1.0%、2.0%）条件下6组混合肥液的电导率，相关结果见图3。当总养分质量分数为1.0%、配比值为（1∶3）～（3∶1）时，6 组混合肥液的电导率从13.46 mS/cm下降至1.80 mS/cm，说明配比值增大会削弱混合肥液的导电能力。当肥液配比值为1 ∶1、总养分质量分数为0.4%～2.0%时，6组混合肥液的电导率从1.49 mS/cm 快速增加到20.13 mS/cm，这表明总养分质量分数的增大对提高混合肥液的导电能力作用明显，主要是因为随着总养分质量分数升高，溶液中的离子数量也会增加。

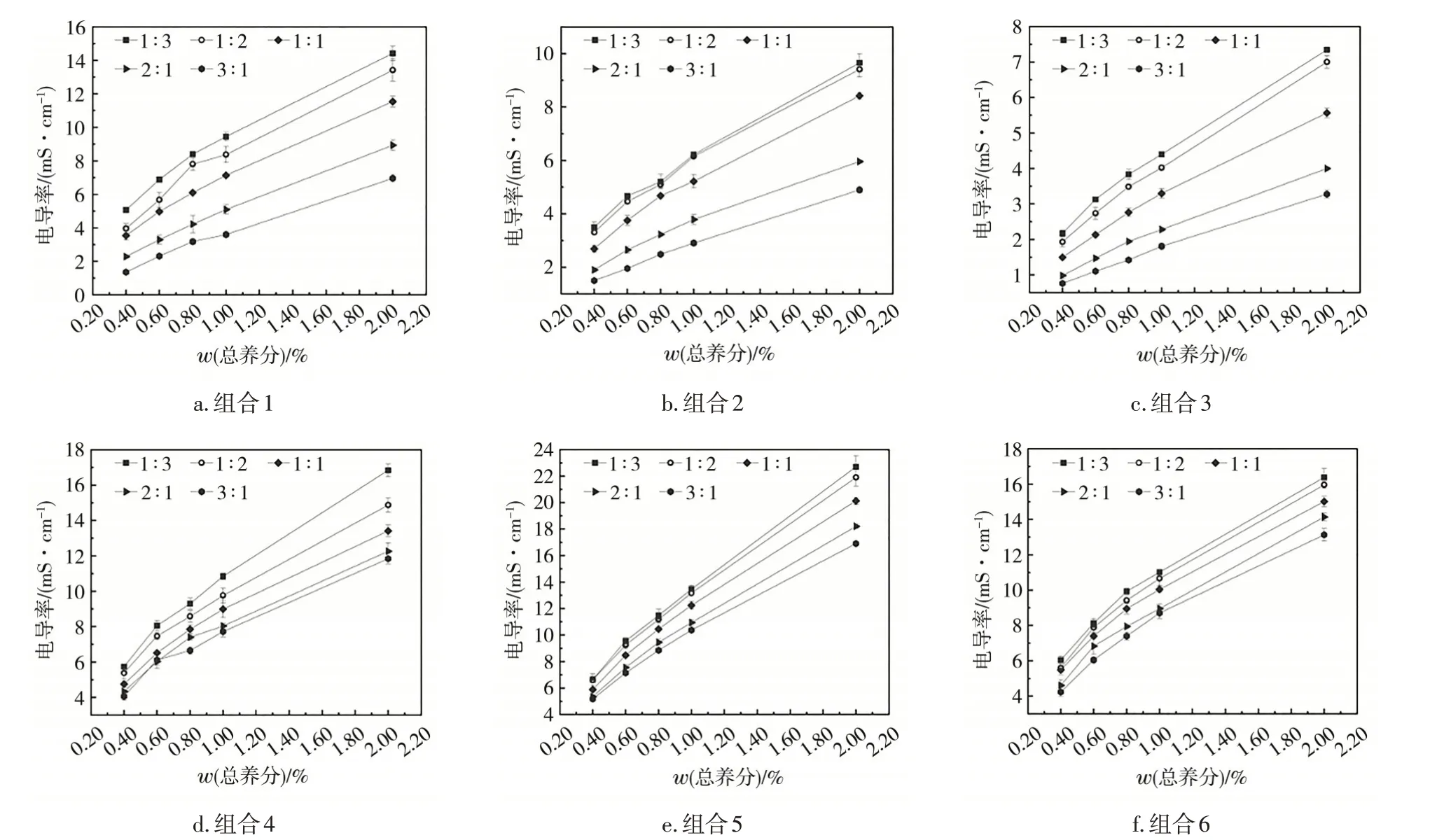
图3 混合肥液不同配比值下总养分质量分数与电导率的关系

为了探究总养分质量分数、配比值耦合作用对混合肥液电导率影响的显著性，以总养分质量分数、配比值作为自变量，电导率为因变量，利用SPSS 26.0对实验数据进行二因素方差分析，结果见表2。由表2 可知，6 组样品p均小于0.01，表明6个组合方差分析模型非常显著；决定系数为1.000，说明6 组混合肥液的电导率能被总养分质量分数、配比值、总养分质量分数和配比值的耦合作用完全解释，且总养分质量分数、配比值、总养分质量分数和配比值的耦合作用对混合肥液的电导率均有极显著影响（p＜0.01），分析结果与图3所示一致。

表2 二因素对混合肥液电导率影响的方差分析结果

为研究总养分质量分数、配比值对混合肥液导电能力影响的相关性，将混合肥液的总养分质量分数、配比值作为自变量，电导率作为因变量，对实验数据进行了相关性分析，分析结果见表3。从表3中可以看出，6组混合肥液的电导率与总养分质量分数极显著正相关（p＜0.01）；此外，6组混合肥液的电导率与配比值极显著负相关（p＜0.01）。

表3 二因素与混合肥液电导率相关性分析结果

2.2 溶液电导率影响因素的影响程度分析

为了量化总养分质量分数、配比值两个变量对混合肥液导电能力的影响，对实验数据进行线性回归分析（见表4）。由表4可知，在以混合肥液电导率为因变量，肥液总养分质量分数、配比值为自变量的线性回归模型中6组混合肥液总养分质量分数的标准化系数均大于配比值的标准化系数，这说明6组混合肥液电导率影响因素的影响程度为总养分质量分数＞配比值。

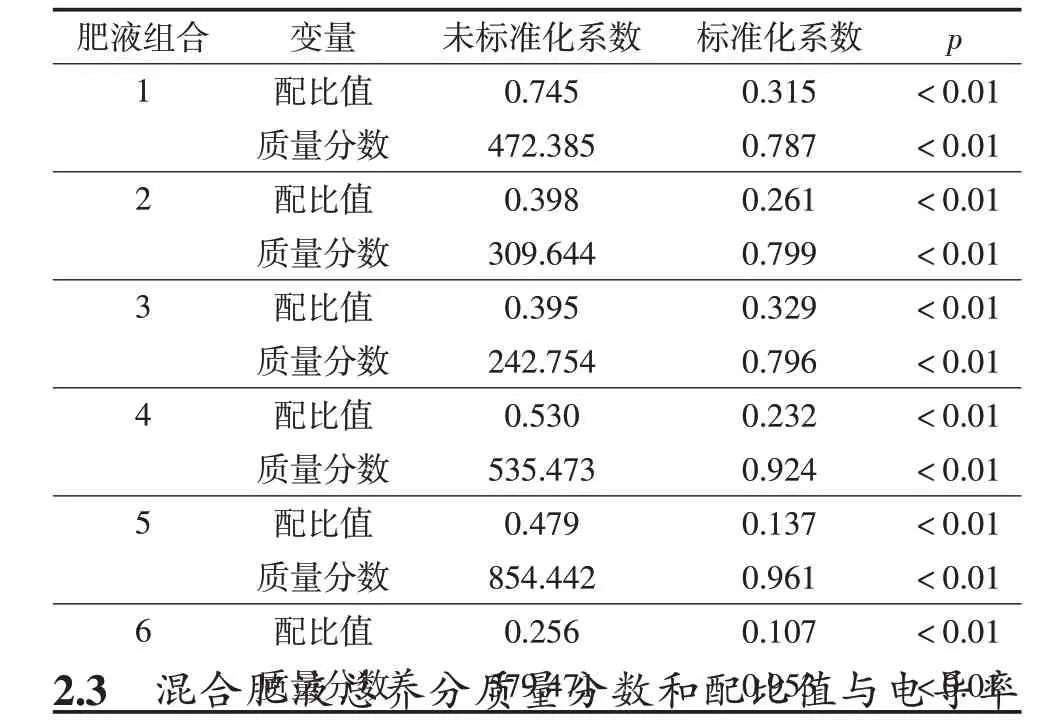
表4 二因素对混合肥液电导率影响程度分析结果

注：p均小于0.01。

2.3 混合肥液总养分质量分数和配比值与电导率之间的关系

将测定得到的一系列散点数据通过Origin 2022进行函数模型拟合，构建包括多元线性回归和非线性曲面拟合两种模型在内的拟合函数集。拟合方程决定系数R2作为筛选指标，筛选结果见表5。从表5中可以看出，6种组合的多元线性回归预测模型的R2均小于非线性曲面拟合预测模型。组合1至组合5混合肥液电导率在配比值和总养分质量分数耦合作用下的变化可以用z=（z0+A01·x+B01·y+B02·y2+B03·y3）/（1+A1·x+A2·x2+A3·x3+B1·y+B2·y2）关联式表达，对应的R2在0.99以上；组合6的电导率在配比值和总养分质量分数耦合作用下的变化关系符合z=z0+a·x+b·y+c·x2+d·y2关联式，其R2在0.98以上。

表5 基于总养分质量分数和配比值耦合作用的混合肥液电导率模型

2.4 模型验证

为了验证函数模型的精度，配制一系列不同总养分质量分数、不同配比值的混合肥液分别测定其在30 ℃时的电导率，实验验证数据及模型精度实验结果分别见表6、表7。

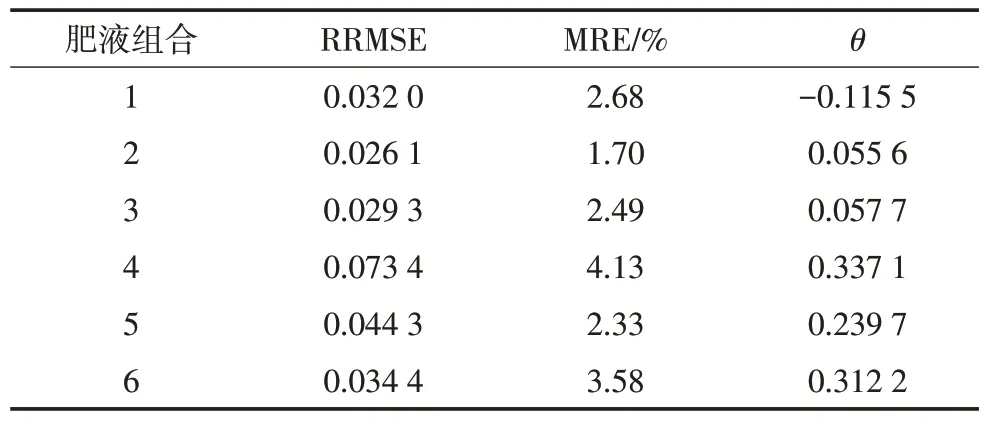
表7 模型精度实验结果

由表7可以看出：组合1的偏差小于0，说明模型预测结果存在低估现象，组合2 至组合6 的偏差均大于0，说明预测结果存在高估现象。6组混合肥液预测模型的相对均方根误差和平均相对误差分别在0.026 1～0.073 4 和1.70%～4.13%范围内，可见6组混合肥液电导率预测模型与实际情况拟合度较高。

3 结论

（1）尿素+氯化钾、尿素+硫酸钾、尿素+磷酸二氢钾、锌工铵+氯化钾、聚磷酸铵+氯化钾、磷酸一铵+氯化钾6 组混合肥液的电导率随着总养分质量分数的增加而增大，随着配比值增大而减小；

（2）6 组混合肥液电导率影响因素的影响程度为总养分质量分数＞配比值；

（3）构建了6 个以混合肥液总养分质量分数、配比值为自变量，电导率为因变量的预测模型。预测平均相对误差分别为2.68%、1.70%、2.49%、4.13%、2.33%和3.58%，在允许范围内。