基于液压支架自主跟机逻辑的移架时长参数设定及动态优化

李 昊，柴保明，翟大磊

（1．中国矿业大学（北京）机电与信息工程学院，北京100083；2．中国煤炭科工集团 北京天地玛珂电液控制系统有限公司，北京100013；3．河北工程大学 材料工程学院，河北 邯郸056038）

自动化采煤技术能够大幅度的提高煤矿开采效率，降低煤矿开采的成本消耗，为煤矿开采行业带来的技术革命。液压支架电液控制系统及其自主跟机控制的应用、与采煤机记忆截割控制的应用一起被视为是综采工作面实现自动化的标志之一[1-2]。液压支架自主跟机是依靠预先设定程序，使液压支架自动完成降、移、升等多个动作顺序，而在这个过程中，判断动作是否完成（到位）是由传感器和时间双参数冗余控制的，传感器数值为优先判断条件，当达到设定的阈值时，自动结束该过程，时间参数为动作保护值，在传感器失效时，或由于外部因素导致动作不到位、传感器检测值不能达到设定的阈值，则需要判断动作执行时长，达到规定时长时也要结束该动作，否则将会影响下一个液压支架的跟机动作[3]。因此，传感器和时长双参数的设定，是液压支架自主跟机逻辑中的核心内容之一，同时，由于传感器的精度、可靠性不一，作为保护的时长参数则尤为重要。然而，液压支架动作时长参数目前多是依靠人工经验进行设定，而且是静态的、不会随着开采过程动态的变化，造成整体的跟机移架速度较慢，自动化生产效率低于人工开采。如何设定移架最长时长参数，以及如何动态的调整该参数，是自主跟机研究中急需研究解决的问题之一。

针对这个问题，目前国内外的研究成果及文献较少，文献[4-8]采用了基于移架机理的研究，通过计算确定移架时长，但实际应用效果不够理想，因为采煤工作面工作条件复杂多变，液压支架移架时长受工作面倾角变化、工作面岩石性质、顶底板破碎程度等因素影响，液压支架移架时的摩擦力阻力各向异性，由于沿倾向每刀煤每个支架受到的摩擦力不一样，每个支架沿走向每刀煤受到的摩擦力不一样，使通过机理研究确定移架时长较为困难[9-10]。为此给出了基于试验的移架时长确定方法，该方法基于历史实际移架时长数据，进行置信区间估计，以确定液压支架移架时长，并可随着生产过程的推进，利用实际数据对模型进行迭代更新以达到动态优化的效果。

1 移架时长确定方法

采煤工作面示意图如图1，随着工作面的推进，每次割煤循环中，每个液压支架都会有1 次移架动作，记移架时长为t，设支架数为n，割煤循环次数为m，则移架时长数据集（m×n 个数据）可表示为矩阵Tmn，则有tij为第i 个支架，割第j 刀煤时的移架时长（i＝1，2，3，…，n；m＝1，2，3，…，m）。

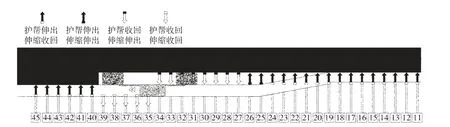
图1 采煤工作面示意图

1.1 试验数据筛选与分布规律

由于煤矿采掘工作面情况复杂，影响移架时长因素比较多。试验数据分布分散，须剔除无效数据。如：对由于液压系统故障、底板岩石摩擦力过大等原因，致使液压支架长时间移动不到位，造成试验数据过大。需根据数理统计理论建立有效的判别方法，予以去除，判别方法如下。

设试验测量得到液压支架跟机移架时长有个试验数据（i＝1，2，…，n），则试验数据的准确度与精密度分别为：

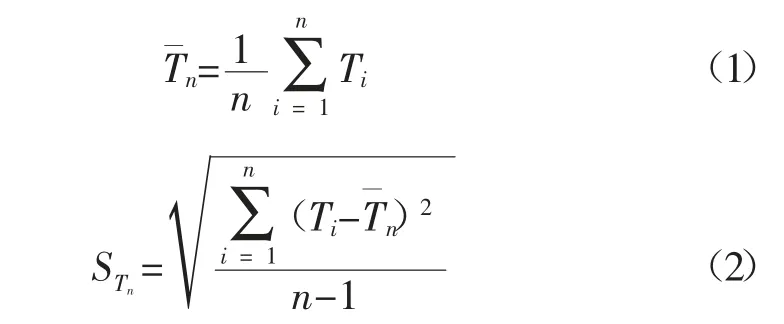
式中：Tn为n 个试验数据的准确度；STn为 精密度；Ti为第i 个试验数据。

1.1.1 试验数据有效性的判别方法

设试验数据符合正态分布，取单侧置信度为（1-0.5α），由试验数据个数n 和t 分布性质，可确定t 分布系数tn-0.5α，由于测试数据数n＞120，t 分布接近于正态分布，t120至t400≈2.32，对数据Ti求ti：

如果：

则表明Ti是非有效数据，需要剔除。剔除后对剩余数据再次计算准确度与精密度，进行有效性判别，直到剔除全部无效数据。若无效数据有r 个，最后对n-r 个有效数据需要计算准确度与精密度。

取α=0.02，即单侧置信度为99%时，分析试验数据的有效性。表明有99%的把握认为剔除的数据是因为意外因素而形成的无效数据。

1.1.2 分布规律的假设检验

根据测得的移架时长数据，通过画频率密度直方图，初步判断数据符合正态分布。对于移架时长是否符合正态分布规律，需运用概率统计原理，对试验数据分布规律进行假设检验。具体步骤如下：

1）假设移架时长试验数据符合正态分布。

2）根据有效试验数据个数n-r，把有效试验数据T1，T2，…，Tn-r分布范围（Ti）max-（Ti）min分为M 个区间，M=1+3.3lg（n-r）并取整数。

3）计算各分区间的理论频数。对于符合正态分布的随机变量T，其统计量Ti，在分组区间[a1，a2]，[a3，a4]，…，[aM，aM+1]内的理论概率分别为Pj，对于n-r个有效试验数据，其统计量Ti落在分组区间[aj，aj+1]内的理论频数为（n-r）×Pj。

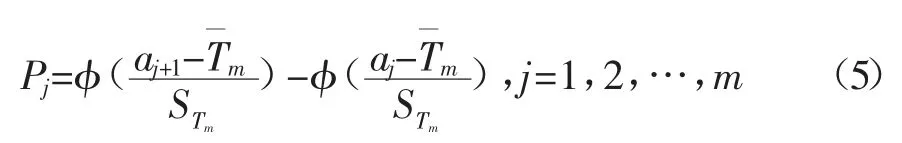
式中：φ（·）为标准正态积分；a1=（Ti）min，aM+1=（Ti）max；（Ti）min、（Ti）max为Ti中的最小值与最大值；aj+1=

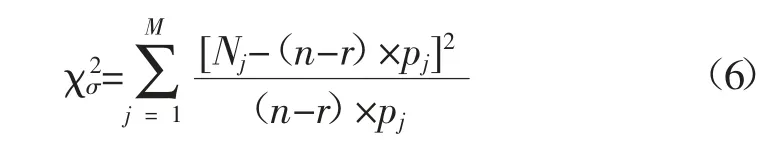
5）确定皮尔逊检验统计量的临界值χ2f，σ，对于M 个区间，取自由度为f=M-1-2，取显著度为δ。根据自由度f 与显著度δ 查表确定χ2f，σ。

1.2 液压支架时长置信区间估计

设液压支架移架时长总体T~N（μ，σ2），来自T样本为：T1，T2，…，Tn，则μ 的置信水平为1-α 的区间估计为：

2 液压支架移架时长测试实例

根据某矿的实测数据进行实例计算，以该矿某工作面使用的ZY6800/11.5/24D 型两柱掩护式液压支架为研究对象，该支架的最小/大高度为1 150/2 400 mm，工作阻力位6 800 kN。针对该综采工作面实际液压支架移架时长数据，进行了现场测试，测试条件为：采煤机速度7.0 m/min，单泵供应流量，泵的流量为400 L。测试液压支架数n 为80，割煤次数m 为5，通过数据前期计算、处理，综采工作面液压支架移架时长部分测试数据（从小到大排列）为：8、8、8、8、8、9、9、9、9、11、11、11、11、12、12、12、12、12、13、13、13、13、13、13、13、13、13、13、13、13、14、14、30、30、30、31、31、31、31、31、31、31、31、31、32、32、32、32、32、33、33、33、34、34、34、34、35、36、37、39、40、58、482、1 052 s。

将测试数据代入式（1）与式（2）可得到400 组移架时长的准确度与精度。由式（3）、式（4）检验第400个移架时长数据T400=1 502，因｜T400｜=19.15＞t399，0.99=2.32，认为该数据为无效数据，从新计算剩余数据的准确度与精密度，再次用式（3）与式（4）检验，直到第392 组移架时长试验数据T392=34 的｜T392｜=2.24＜t391，0.99=2.32，因此表明是有效的。

假设移架时长Tm基本符合正态分布，对于392组移架时长Tm的有效试验数据，由1+3.31g392=9.55，确定M=10，将其分为10 个区间，自由度为f=10-1-2=7，取显著度，δ=0.05。

查表得皮尔逊检验统计量的允许值χ27，0.95=14.067，计算每个分组区间实际频数（Nj）与皮尔逊检验统计量，移架时长的皮尔逊统计量χ2见表1。

由式（7），可求出置信度为0.95 的置信区间估算，由于样本大于400，样本数较大，认定t 分布趋向于正态分布，查表取=1.96：

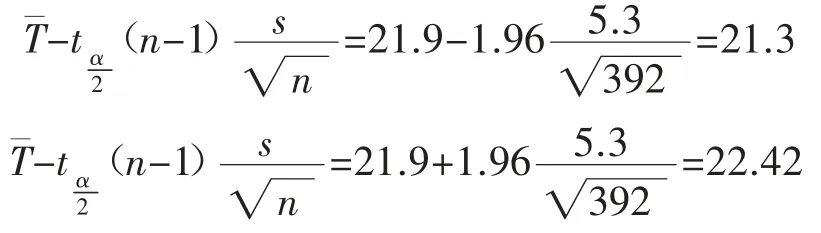
即移架时长的置信水平为95%的区间估计为[21.3，22.42]，工程上认为95%置信水平条件下，对数据估值是准确的，确定移架时长为22 s。

3 模型的动态优化和验证

1）动态优化。由于地质条件等环境因素的影响，综采工作面生产过程是动态变化的，因此，上述确定移架跟机时长参数的方法也需要根据生产情况的变化而动态优化。模型动态优化过程示意图如图2，其中，通过液压支架电液控制器实时采集实际移架时长，并将数据传输至监控中心上位机中，由上位机中的软件进行数据的筛选以及前文所述的算法计算，最终确定液压支架自主跟机逻辑中的移架时长参数。同时，上位机将原始数据以及计算结果数据存入至数据库中，随着工作面的推进，这些数据与新产生的数据一起作为新的训练样本，对模型进行迭代训练，以此，达到模型的动态优化。

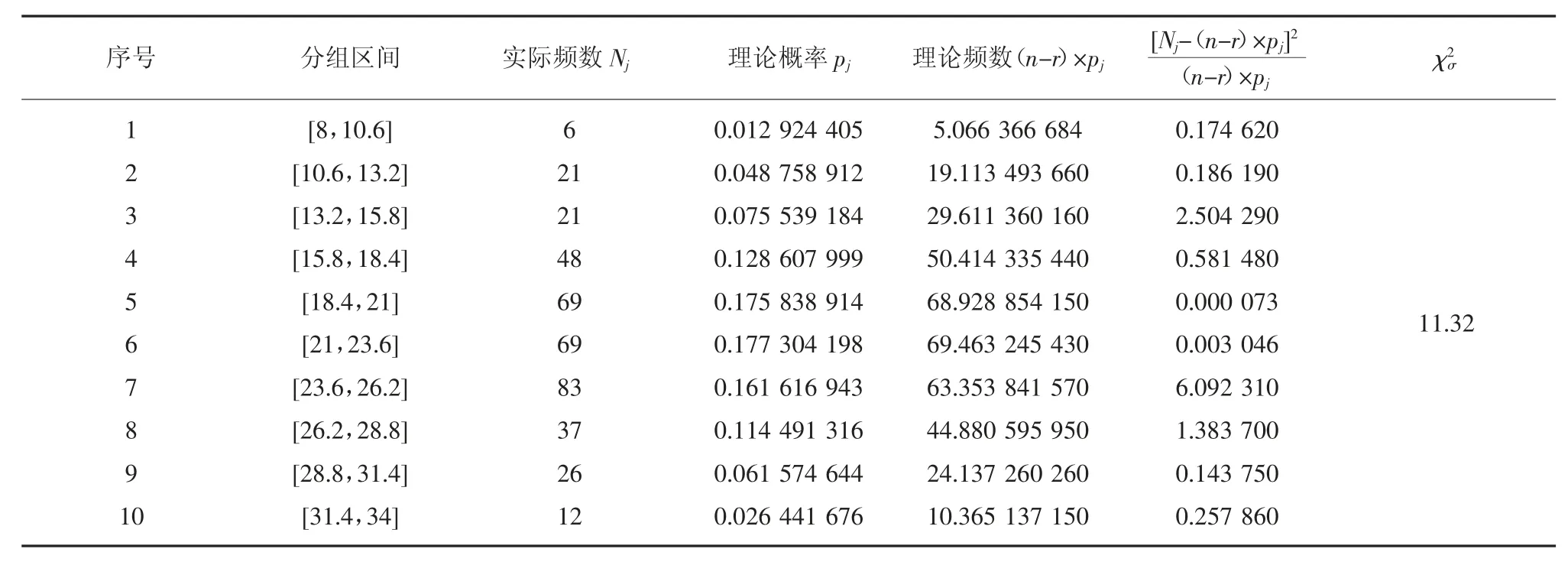
移架时长的皮尔逊统计量χ2

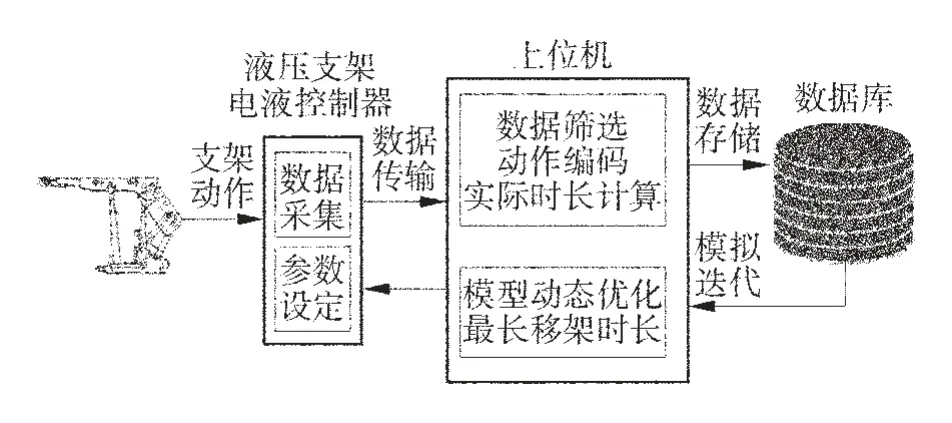
图2 模型动态优化过程示意图

2）模型验证。在试验矿井的另一个综采工作面进行了实际的模型验证，该工作面倾斜长150 m，安装了相同架型综采液压支架100 个，工作面初采时，采用上述方法确定支架移架初始时长，结合采煤机割记忆截割示范刀时，同时收集移架时长数据，经去除无效数据，数据分布假设检验，对移架时长进行置信区间估计，得到移架时长的置信水平为95%的区间估计为[15.28，15.91]，确定移架初始时长为15 s。解决了由于初始值设置不准导致工作面初采时，移架混乱的问题，并为工作面移架时长的进一步修正提供了依据。

4 结 语

给出了基于生产实测数据的移架时长计算方法，其特点为应用简单，确定的数据准确。而且，以此试验数据为依据，能分析判断出供液系统和采煤机割煤工艺质量以及顶板状况存在的问题，提出相应改进改进措施，缩短移架时长。经实际应用，获得了好的效果,为下一步建立数据库，形成基于机器学习的移动时长确定方法，实现采煤工作面自动化、智能化奠定了数据基础。