岩体孔隙-裂隙双渗流数值模拟研究
2019-09-27邵建立薛彦超杜后谦
邵建立,周 斐,薛彦超,杜后谦
(山东科技大学 矿业与安全工程学院,山东 青岛266590)
岩体渗流一直是矿山、水利水电、建筑等岩土工程的重要问题,流体在岩体裂隙中快速运移,也会相对缓慢的通过周围基质块中微小孔隙迁移。采取合理的防渗措施是防控岩体渗流危害的有效手段,而准确地选取理论模型进行计算和模拟是预防和消除岩体渗流影响的关键[1-2]。基于岩体具有裂隙和基质双重渗流过程,研究孔隙-裂隙双重介质渗流场发展变化规律尤为重要。
国内外学者已经针对裂隙岩体渗流特征进行了许多相关的研究。朱斌[3]等结合开滦赵各庄矿14 水平开拓东大巷揭露的薄层煤岩体渗流演化过程进行数值模拟,通过调节渗透系数,获得了薄层煤岩体裂隙-孔隙双渗流在时间和空间上的孔隙水压变化过程;速宝玉[4-6]等通过实验研究裂隙岩体渗流应力耦合情况,阐明了单裂隙面的各种经验公式、间接公式及其适用条件,分析了裂隙岩体渗流应力耦合模型优缺点及目前工程应用情况。李琛亮[7]等研制的双重介质渗流水力特性试验系统,研究了基于双重介质模型的水量交换以及渗流场的水压分布规律以及双重介质的水力性态和渗流机制,得出孔隙-裂隙双重介质水交换影响因子对双重介质水交换的影响能力;国外Barenblatt 提出均质、各向同性的孔隙-裂隙双重介质概念[8],后续学者们开展了孔隙-裂隙双重介质模型及其解析和数值算法[9-10]。Samardzioska[11]比较了岩体等效介质模型、裂隙网络模型和裂隙-孔隙双重介质模型的渗流演化规律,获得了不同介质假设下岩体渗流演化对比研究成果。
由于岩体内部不可视性和裂隙网络错综复杂,学者们难以可视化地揭露内部孔隙-裂隙渗流规律变化。基于此,采用多孔介质渗流数值模拟的方法,建立断裂的多孔介质块模型,通过不同形状路径的裂隙,对孔隙-裂隙双重介质渗流场分布进行模拟研究,以期为揭露岩体渗流规律、渗流危害预测与防治提供一定的理论支持。
1 孔隙-裂隙渗流数值模拟
1.1 基本控制方程
1.1.1 孔隙渗流方程
流体在均质的基质块中渗流遵循达西定律[9],随时间变化的方程为:
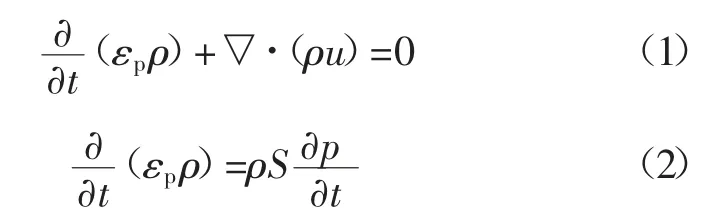
式中:u 为速度矢量,m/s;p 为孔隙水压力,Pa;εp为基质块的孔隙率;S 为基质块储水系数,1/Pa;ρ为密度,kg/m3;t 为时间。
线性储水模型为:
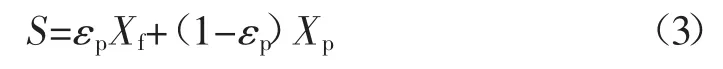
式中:Xf为流体压缩率,1/Pa;Xp为基质块等效压缩率,1/Pa。
在块内,内建的速度变量u 给出达西速度,达西速度是多孔介质单位面积的体积流量。

式中:k 为基质块的渗透率,m2;μ 为流体动力黏度,Pa·s。
1.1.2 裂隙渗流方程
使用COMSOL 裂缝流边界条件,允许沿着内部边界或裂隙定义流动。在这种边界条件下,裂隙速度方程遵循基质块内速度方程(即达西定律)的修正形式。考虑到裂隙对流动阻力较小,裂隙厚度较小,使得裂缝与基体的尺寸一致性,对达西定律修正,得到以下方程:
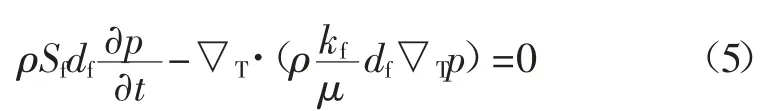
式中:Sf为裂隙储水系数,1/Pa;kf为裂隙的渗透率,m2;df为裂隙厚度,m;▽T为裂隙切向平面的梯度算子。
由于裂缝流动方程中含有厚度,内建变量uf给出了裂隙单位长度的体积流量:

式中:uf为裂隙速度矢量,m/s。
1.2 模拟方案
使用COMSOL 数值模拟软件对孔隙-裂隙双渗流进行数值模拟。岩体孔隙-裂隙双渗流数值模拟模型如图1。物理模型为4 种断裂的均质的多孔介质块,块体每边长度为1 m。块中为不同形状路径的裂隙,依次为90°夹角型、45°夹角型、135°夹角型、圆角型。与孔隙渗流相比,裂隙对流体的渗透性更强,同时裂隙厚度为0.1 mm,远小于块的尺寸。流体从右向左移动,通过块进入裂隙下部边界并从上部边界离开。流体最初不在块内渗流。出口边界处的压力随时间下降,而入口边缘处的压力在整个模拟过程中保持初始压力。
除了在裂隙边界之外,基质块的壁是不可渗透的。沿块体的所有面应用0 流量边界条件:

式中:n 为向外指向边界的法向量。
在裂隙入口和裂隙出口,采用压力边界条件,关系式如下(0≤t≤1 000 s):

式中:p 为裂隙出口压力,Pa;p0为裂隙入口压力,Pa;t 为时间,s;a 为压力变化率,Pa/s。
本次数值模拟的相关参数和赋值见表1。
2 模拟结果分析
2.1 裂隙流动分析
以90°角裂隙模拟为例分析裂隙流动变化。不同时刻裂隙路径速度分布如图2。随着时间的变化,出口边界的压力呈线性减少,而入口边界的压力保持恒定p0,产生的压力差驱使流体流动,裂隙上的速度分布逐渐改变。可以发现,计算刚开始速度分布均匀,随着压力差增大,速度场也发展增大。当计算达到1 000 s,入口边界和出口边界压力差达到最大值,速度场也发展到最大值。其次,流体从裂隙入口到出口,其速度是线性连续的,其中在向上导升过程中部分动能转化为势能,速度变化微小,而在入口边界和出口边界的速度始终是流场中的最大值。

表1 数值模拟相关参数和赋值

图2 不同时刻裂隙路径速度分布
2.2 基质孔隙流动分析
以90°角裂隙模拟为例分析内部流动。不同时刻基质块内部压力等值面分布如图3。随着时间变化,出口压力逐渐减小,整个基质块内部孔隙压力重新分布,压力等值面分级增多,高压等值面靠近入口,低压等值面靠近出口,基质块内部压力梯度越来越显著。同时等压面穿过裂隙,表明压力分布在断裂的基质块中是连续的,因此裂隙上压力分布也是连续。但在压力等值面与裂隙相交处具有不同程度的弯折,联合图2 可发现,裂隙速度越大压力等值面弯曲越明显,表明流体在裂隙和孔隙中的流动状态不同。
2.3 不同路径裂隙流动对比分析
对于4 种不同断裂形状的多孔介质块,保持相同初始参数和边界条件模拟,分别在4 种模型种选取x=0.5 m 处yz 截面,以1 000 s 计算为例,绘制速度等值线并填充(图4)。

图3 不同时刻基质块内部压力等值面分布
由图4 可以看出,速度场基本在截面上呈中心对称分布,且不同路径的裂隙对孔隙渗流速度影响是不同的,在45°、90°、135°角形状裂隙路径中,夹角处均出现了较小的相对高速区域,图4 圆角则没有出现这种相对高速区域,原因是在夹角处流体的流动方向突然发生改变,产生了局部阻力损失,而缓和的路径减少了这种能量损失,圆角型裂隙流体在出口处速度比其他路径裂隙出口速度都高,达到2.59×10-4m/s。

图4 不同断裂形状的基质块截面速度分布
沿不同形状路径裂隙出口边界上,不同时刻流体边界通量分布如图5。流体边界通量是指单位时间内流经边界单位面积的物质量,是表示输送强度的物理量。本次模拟中,除了裂隙形状不同,其余参数保持相同,因此出口边界通量可以反映不同路径裂隙情况下流体流动的强度或速度。从图5 中看出,起始阶段不同形状裂隙的边界通量相差微小甚至相交,因为初始阶段入口和出口的压力差不大,流体运动缓慢,随着时间增加,速度场逐渐发展,不同路径裂隙渗流的能量损失逐渐明显,同时不同路径裂隙的边界通量也呈线性增长趋势。当计算至1 000 s时,圆角型和135°夹角型路径裂隙具有较高的边界通量,表示渗流过程中流体能量损失较小,而圆角型路径裂隙边界通量最高,说明圆角型路径裂隙流体能量损失最小;90°夹角型和45°夹角型路径裂隙边界通量较小,表示这2 种路径渗流过程能量损失较大,其中45°夹角型边界通量最小,说明渗流过程能量损失最多。

图5 不同时刻4 种裂隙出口边界通量变化
3 结 论
1)裂隙是渗流的主要途径,在压力充足的情况下,流体在裂隙流动发展最充分,渗流场在裂隙路径上连续分布。在矿山深部和地下岩土工程等具有高水压威胁的地方,裂隙渗流的影响不可忽视,应从裂隙渗流角度防控灾害。
2)各向同性的多孔介质内部孔隙压力梯度分布均匀,断裂的多孔介质块压力分布是连续的,裂隙和孔隙存在流体交换,这取决于流场内压力分布。由于裂隙和孔隙具有不同的渗透率等因素,流体在裂隙和孔隙的流动状态明显不同。
3)不同形状路径的裂隙渗流场也有差异。保持相同初始参数,4 种路径裂隙出口边界流体通量在起始阶段相差微小,随着时间变化速度场充分发展,这种差距愈加明显,到1 000 s 时,4 种裂隙出口边界通量的大小关系为:圆角型>135°夹角>90°夹角>45°夹角,说明4 种路径裂隙的能量损失大小关系为:45°夹角>90°夹角>135°夹角>圆角型。

