高煤阶煤层气储层毛管压力数学模型适应性评价

曾建强，华 彬，谭政林

（1.成都理工大学 沉积地质研究院，四川 成都610059；2.四川京川大正油田技术服务有限责任公司，四川 成都610059）

煤层气储层毛管压力对煤层气产出具有重要的意义[1]，煤岩毛管压力曲线对煤层气储层评价，尤其对孔隙结构定量评价具有重要的意义[2]。目前关于毛管压力数学模型的研究多基于常规储层压汞实验，如杨宇等认为Brooks-Corey 模型仅适用于渗透率较高的砂岩储层，并基于分形理论提出了适用于致密砂岩储层的毛管压力计算模型[3]。刘银山认为Brooks-Corey 模型适用于均质储层，而Li-Horne 模型均质、非均质储层均适用[4]。陶正武认为Brooks-Corey 模型和Gerhard-Kueper 模型适用于常规储层毛管压力曲线[5]。而关于煤层气储层毛管压力曲线数学模型的研究较少，杨宇等基于分形理论推导了一种煤岩毛管压力曲线[6]。袁哲等认为现有毛管压力模型不适应与煤岩，提出了一种新的毛管压力数学模型[7]。目前高煤阶煤岩缺乏有效的毛管压力曲线数学模型，压汞实验数据难以有效拟合，导致毛管压力实验数据难以进一步应用于渗透率、相对渗透率等关键参数的定量计算。基于沁水盆地南部高煤阶储层煤样高压压汞实验，分析现有的经典的毛管压力曲线数学模型对高煤阶煤岩的适用性，以期找到适用于煤煤层气储层的毛管压力数学模型。

1 毛管压力曲线数学模型

1）Corey 模型。Corey（1954）提出了定量计算砂岩毛管压力曲线的模型[8]：

式中：pc为毛管压力；C 为常数；Sw*为归一化湿相饱和度。

2）Thomeer 模型。Thomeer（1960）提出了利用进汞饱和度计算毛管压力的模型[9]：

式中：pe为排驱压力，即非润湿相进入岩心最大孔隙时所对应的毛管压力值；SHg为进汞饱和度；SHg∞为最大毛管压力处进汞饱和度；Fg为孔隙几何因子。

3）Brooks-Corey 模型。Brooks 和Corey（1964）在Corey 模型的基础上提出了Brooks-Corey 模型[10]：

式中：λ 为孔隙大小分布指数。

4）贺承祖模型。贺承祖等（1998）推导出通过砂岩压汞曲线度量砂岩孔隙结构分形特征的模型为[11]：

式中：Sw为湿相饱和度；Df为分形维数。

5）Li 模型。Li（2004）提供了更为一般化的毛管压力模型[12]：

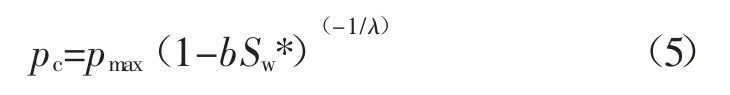
式中：pmax为残余湿相饱和度下的毛管压力；b为常数。

2 高压压汞实验

2.1 实验准备及步骤

选取沁水盆地南部晋城矿区高煤阶煤岩样品，将煤岩加工成直径25 mm、长度50 mm 的煤柱，选取其中7 块外观完整的煤岩样品。

利用气体渗透率仪、孔隙度仪分别测定7 块煤岩样品渗透率和孔隙度，实验煤样基本参数见表1。利用PoreMaster-60 型全自动压汞仪测定7 块煤岩样品的毛管压力曲线，实验煤样毛管压力曲线如图1。所有实验在20℃下进行。

2.2 实验结果

表1 表明，7 块煤岩样品孔隙度分布在1.5%～8.6%之间，渗透率分布在0.02×10-15～0.98×10-15m2之间，为低孔低渗储层。

图1 表明，7 块煤岩样品毛管压力曲线形态差异较大，煤样2 进汞饱和度最小，毛管压力曲线陡峭，物性极差，为III 类储层；煤样3、煤样5 和煤样6进汞饱和度较大，毛管压力曲线存在中间平缓段，渗透率高于0.25×10-15m2，物性条件相对较好，属于I类储层；其余煤样毛管压力曲线介于二者之间，为II类储层。

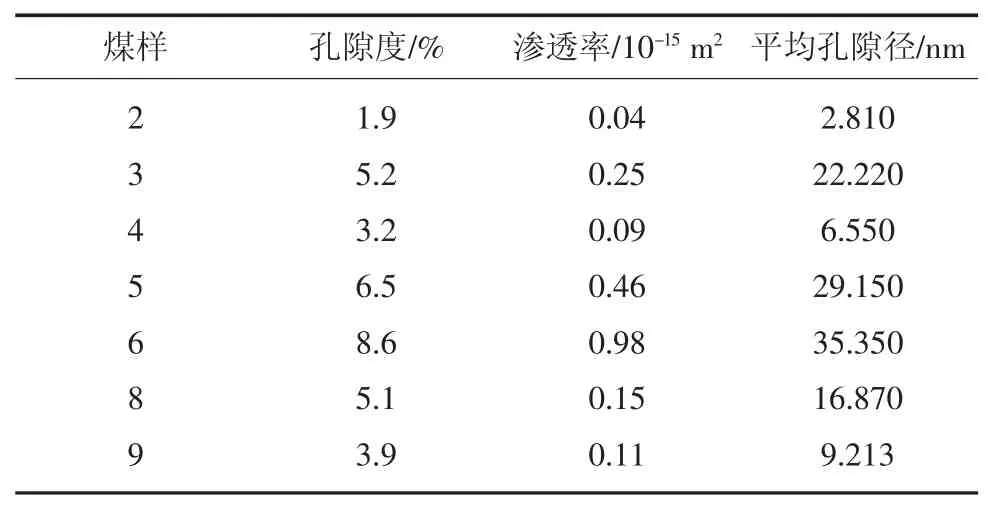
表1 实验煤样基本参数

图1 实验煤样毛管压力曲线

3 适应性评价

3.1 Corey模型

对式（1）两边取对数，整理得：

由式（6）可知，如果煤岩毛管压力曲线满足Corey模型，则在双对数坐标中，归一化湿相饱和度Sw* 和毛管压力pc成线性关系，且斜率为-1/2。归一化煤样湿相饱和度与毛管压力间关系如图2。图2 表明，在双对数坐标系中，归一化湿相饱度和毛管压力并非成线性关系，且曲线与斜率为-1/2 的曲线并不平行，表明煤岩毛管压力曲线模型不符合Corey 模型。

3.2 Thomeer模型

对式（2）两边取对数，整理得：

由式（7）可知，如果煤岩毛管压力曲线满足Thomeer 模型，则在双对数坐标中，进汞饱和度SHg和毛管压力pc成线性关系，且斜率为-。煤样进汞饱和度与毛管压力关系如图3。

图2 归一化湿相饱和度与毛管压力间关系

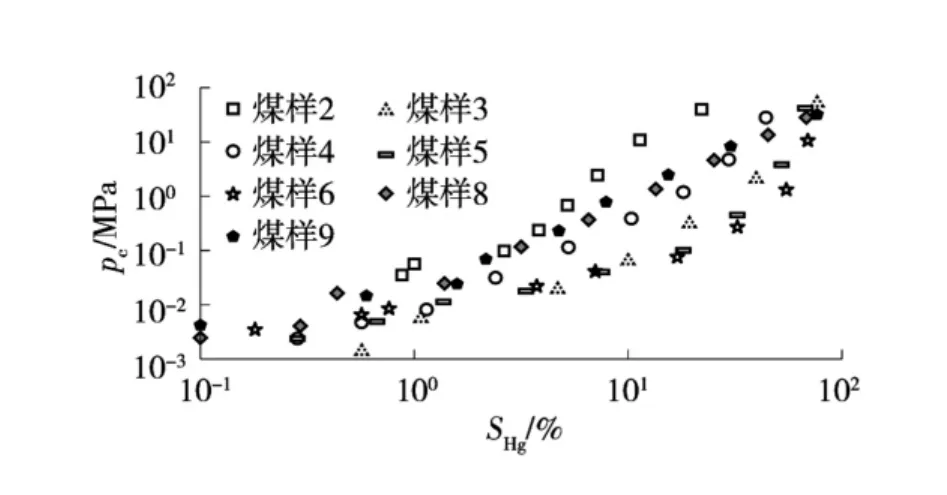
图3 煤样进汞饱和度与毛管压力间关系

图3 表明，在双对数坐标系中，进汞饱和度和毛管压力并不总是线性关系，煤样4、煤样8、煤样9的进汞饱度与毛管压力成线性关系，其余煤样并非线性关系，表明Thomeer 模型只适用于孔、渗条件适中的II 类储层，而不能有效拟合全部高煤阶煤岩毛管压力曲线。

3.3 Brooks-Corey模型

对式（3）两边取对数得到：

由式（8）可知，如果煤岩毛管压力曲线满足Brooks-Corey 模型，则在双对数坐标中，毛管压力与标准化湿相饱和度成线性关系，斜率为-，截距为lgpe。煤样湿相饱和度与毛管压力间关系如图4。图4 表明在双对数坐标中，pc与Sw* 并不成线性关系，因此煤岩毛管压力曲线不符合Brooks-Corey模型。

3.4 贺承祖模型

将式（4）两边取对数，得到：

Df和pe为常数，由式（9）可知，如果煤岩孔隙结构具有分形特征，则在双对数坐标中，Sw-pc为一直线，直线段的斜率为Df-3。图4 表明，在双对数坐标系中，湿相饱和度和毛管压力并不总是线性关系，煤样5 和煤样6 的湿相饱和度与毛管压力成线性关系，其余煤样并非线性关系，表明贺承祖模型具有适用条件，只适用于孔渗条件较好的I 类储层，不能用于全部高煤阶煤层气储层。

图4 煤样湿相饱和度与毛管压力间关系

3.5 Li模型

将式（5）整理得，

根据式（10），将归一化湿相饱和度对毛管压力微分，并两边取对数得：

由式（11）可知，如果煤岩毛管压力曲线满足Li模型，则在双对数坐标中，dSw*/dpc与毛管压力成线性关系，斜率为-λ-1。煤样dSw*/dpc与毛管压力间关系如图5。图5 表明，在双对数坐标中，dSw*/dpc与pc均成线性关系，因此煤岩毛管压力曲线符合Li 模型。

图5 煤样dSw*/dpc 与毛管压力间关系

Li 模型的主要参数为b 和λ，根据式（11），λ 可以通过下式计算：

式中：k 为dSw*/dpc与毛管压力拟合直线的斜率。

根据式（11），b 可由下式计算：

式中：a 为dSw*/dpc与毛管压力拟合直线的截距。

将图5 数据进行线性回归，得到回归直线的斜率k 和截距a，然后根据式（12）和式（13）计算煤样Li 模型的主要参数b 和λ，煤样Li 模型拟合参数见表2。利用计算参数对实验数据进行拟合，相关度均在0.95 以上，表明Li 模型及参数求解方法适用于高煤阶煤岩毛管力曲线。

表2 煤样Li 模型拟合参数

4 结 论

1）在双对数坐标中，归一化湿相饱度和毛管压力并非成线性关系，且曲线与斜率为-1/2 的曲线并不平行，表明高煤阶煤岩毛管压力曲线模型不符合Corey 模型，也不符合Brooks-Corey 模型。

2）在双对数坐标中，II 类储层煤岩样品的进汞饱和度和毛管压力成线性关系，因此，Thomeer 模型只适用于孔、渗条件适中的II 类储层。在双对数坐标中，I 类储层煤岩样品的湿相饱和度和毛管压力成线性关系，因此，贺承祖模型只适用于孔渗条件较好的I 类储层。

3）在双对数坐标中，dSw*/dpc与pc均成线性关系，Li 模型适用于全部高煤阶储层。利用式（12）和式（13）计算得到b 和λ，能够有效拟合实验数据。