函数测试题A 卷参考答案

一、选择题

1.D 2.C 3.B 4.D 5.C 6.B

7.B 8.C 9.C 1 0.C 1 1.D 1 2.C

二、填空题

13.{x|x＞-2,且x≠2} 1 4.-3

三、解答题

18.(1)函数f(x)=ax+b(a＞0,a≠1),其中a,b均为实数,函数f(x)的图像经过点A(0,2),B(1,3),所以所以所以函数f(x)=2x+1＞1,函数y=,故函数的值域为

(2)如果函数f(x)的定义域和值域都是[-1,0]。

若a＞1,函数f(x)=ax+b为增函数,所以求得a,b无解。

若0＜a＜1,函数f(x)=ax+b为减函数,所以求得所以a+

19.(1)H,H(0)的实际意义为不使用新型隔热材料时,每年的能源消耗费用为8万元。所以f(x)的解析式为f(x)

若不使用隔热材料,则2 0年的能源消耗总费用为8×2 0=1 6 0万元,故业主可节省9 0万元。

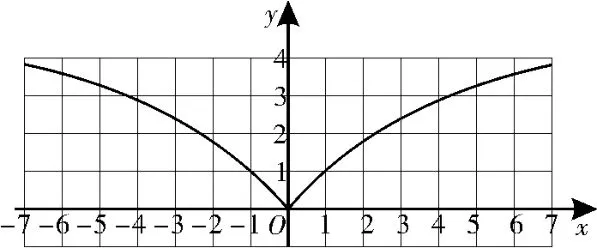
图1

(1)函数g(x)=f(1+x)+f(1-x)=log2(1+x)+log2(1-x)=log2(1-x2)的定义域为(-1,1),关于原点对称,且g(-x)=g(x),故g(x)为偶函数。

又1-x2∈(0,1],故g(x)∈(-∞,0],即g(x)的值域为(-∞,0]。

(2)若关于x的方程f(x2-t x+8)=2在[1,4]上有解,即x2-t x+8=4,即x2-t x+4=0在[1,4]上有解,即在[1,4]上有解。

由对勾函数的图像和性质可得:

22.(1)由题意可知,a2-2a-2=1,a＞0且a≠1,解得a=3,所以f(x)=log3x。

因为g(x)=log3(x+1)+log3(3-x),所以所以,即()的-1＜x＜3gx定义域为(-1,3)。

由于g(x)=log3(x+1)+log3(3-x)=log3(-x2+2x+3),令u(x)=-x2+2x+3(-1＜x＜3),由对称轴x=1可知,u(x)在(-1,1)上单调递增,在(1,3)上单调递减。又因为y=log3u(x)在(0,+∞)上单调递增,故g(x)的单调递增区间为(-1,1),单调递减区间为(1,3)。