导数易错题归类剖析

■河南省太康县第一高级中学

导数的几何意义问题的类型主要有:一是利用导数求曲线的切线方程;二是判断直线与曲线的位置关系;三是研究切线的斜率或倾斜角。题型主要是选择题或填空题,文科试卷大多是命制导数的几何意义、利用导数研究函数的性质综合问题。

导数应用的综合问题的类型主要有:一是利用导数求函数的单调区间或判断函数的单调性,求函数的极值或最值;二是利用导数解决与函数零点有关的问题;三是利用导数解决不等式和求参数范围的问题。通过函数与导数综合考查单调性和最值问题仍然是热点,也是难点。选择题、填空题往往侧重于利用导数确定函数的单调性和极值,一般属于低档题目;解答题侧重于导数与函数、解析几何、不等式、数列等知识的综合应用,一般难度较大,属于中高档题。

例1 曲线在点(1,2)处的切线方程为____。

易错点：函数求导公式不正确,直线方程书写不规范。

解析：设y=f(x),则所以f'(1)=2-1=1,所以曲线在点(1,2)处的切线方程为y=x+1。

例2 已知曲线,求曲线过点P(2,4)的切线方程。

易错点：易忽视“曲线过点P(2,4)的切线方程”与“该曲线在点P(2,4)处的切线方程”的区别,导致漏解。

解析：设曲线与过点P(2,4)的切线相切于点,则切线的斜率k=y'|x=x0=x20,所以切线方程为

因为点P(2,4)在切线上,所以4=,即,所以,所以(x0+1)(x0-2)2=0,解得x0=-1或x0=2,故所求的切线方程为4x-y-4=0或x-y+2=0。

例3 若直线y=k x+b是曲线y=的切线,也是曲线y=ln(x+1)的切线,则b=____。

易错点：两个曲线的切点不是同一个点,应该分别设出来。

解析：对函数y=lnx+2求导得y'=,对y=ln(x+1)求导得设直线y=k x+b与函数y=lnx+2相切于点与函数y=ln(x+1)相切于点则y1=lnx1+2,y2=ln(x2+1)。因为点P1(x1,y1)在切线上,所以y-,由点P2(x2,y2)在切线上得),这两条直线表示同一条直线,所以解得x1=,所以,所以

方法归类：与导数几何意义有关问题的常见类型及解题策略:

(1)已知切点求切线方程。解决此类问题的步骤为:

①求出函数y=f(x)在点x=x0处的导数,即曲线y=f(x)在点P(x0,f(x0))处切线的斜率;

②由点斜式求得切线方程为y-y0=f'(x0)·(x-x0)。

(2)已知斜率求切点:已知斜率k,求切点(x1,f(x1)),即解方程f'(x1)=k。

(3)求切线倾斜角的取值范围:先求导数的取值范围,即确定切线斜率的取值范围,然后利用函数的单调性解决。

例4 已知函数f(x)=ae2x+(a-2)·ex-x。

(Ⅰ)讨论f(x)的单调性;

(Ⅱ)若f(x)有两个零点,求a的取值范围。

易错点：第一,牢记求导法则,正确求导:在函数与导数类解答题中,通常都会涉及求导,正确的求导是解题关键,因此要牢记求导公式,做到正确求导,解题时应先写出函数的定义域。

第二,注意利用第一问的结果:在题设条件下,如果第一问的结果第二问能用得上,可以直接用,有些题目不用第一问的结果甚至无法解决,如本题的第二问就是在第一问的基础上求解的。

第三,注意分类讨论:高考中的函数与导数解答题,一般都会涉及分类讨论,并且讨论的步骤也是得分点,所以一定要重视分类讨论。

第四,写全得分点:在函数与导数问题中,求导的结果、分类讨论的条件、单调区间、零点等一些关键式子和结果都是得分点,在解答时一定要写清楚。

解析：(Ⅰ)f(x)的定义域为(-∞,+∞),f'(x)=2ae2x+(a-2)ex-1=(aex-1)(2 ex+1)。

(1)若a≤0,则f'(x)＜0,所以f(x)在(-∞,+∞)上单调递减。

(2)若a＞0,则由f'(x)=0得x=-lna。

当x∈(-∞,-lna)时,f'(x)＜0;

当x∈(-lna,+∞)时,f'(x)＞0。

所以f(x)在(-∞,-lna)上单调递减,在(-lna,+∞)上单调递增。

(Ⅱ)(1)若a≤0,由(Ⅰ)知,f(x)至多有一个零点。

(2)若a＞0,由(Ⅰ)知,当x=-lna时,f(x)取得最小值,最小值为f(-lna)=1-

①当a=1时,由于f(-lna)=0,故f(x)只有一个零点;

②当a∈(1,+∞)时,由于＞0,即,故f(x)没有零点;

③当a∈(0,1)时,即e-2+2＞-2 e-2+2＞0,故f(x)在(-∞,有一个零点。

设正整数n0满足,则

综上,a的取值范围为(0,1)。

点评：本题主要考查导数的运算及导数的应用,函数的单调性,函数的零点等知识,意在考查考生的运算求解能力、分析问题与解决问题的能力。第(Ⅰ)问对函数求导,导函数含有参数,需要对参数进行分类讨论,再判断函数的单调性;第(Ⅱ)问结合第(Ⅰ)问函数的单调性,判断函数存在两个零点的条件,进而确定参数的范围。

跟踪训练：

1.曲线y=-ex+3在点(0,2)处的切线与直线x=0和y=2x所围成的三角形面积为( )。

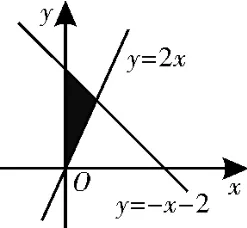
图1

解析：由y=-ex+3,得y'=-ex,则y'|x=0=-1,所以曲线y=-ex+3在点(0,2)处的切线方程为y=-x+2,如图1,联立解得所以所求三角形面积为故选B。

2.已知定义域为(1,+∞)的函数f(x)=ex+a-a x,若f(x)＞0恒成立,则正实数a的取值范围为( )。

解析：根据题意,f(x)=ex+a-a x,若f(x)＞0恒成立,只需恒成立,设则

分析可得,在(1,2)上,g'(x)＜0,g(x)为减函数,在(2,+∞)上,g'(x)＞0,g(x)为增函数,可知当x=2时,g(x)取得最小值e2,所以a＜e2。又因为a＞0,所以a的取值范围是(0,e2)。故选B。

3.已知a,b为正实数,直线y=x-a+2与曲线y=ex+b-1相切,则的最小值为( )。

A.1 B.2 C.4 D.8

解析：由y=x-a+2得y'=1;由y=ex+b-1得y'=ex+b。因为直线y=x-a+2与曲线y=ex+b-1相切,令ex+b=1,可得x=-b,代入y=ex+b-1得y=0,所以切点为(-b,0),则-b-a+2=0,所以a+b=2。所以,当且仅当a=b=1时等号成立,此时取得最小值2。故选B。