基于稳定气流法对莱氏现象的探究

吕承昊 吕钧霆 刘世元

(山东省青岛第二中学，山东 青岛 266100)

1 概述

1756年，莱顿弗罗斯特(Leidenfrost)在红热的金属汤匙上滴下一滴水，水珠在汤匙上悬浮了近30秒钟，而没有蒸发。莱顿弗罗斯特对这种现象非常感兴趣，并进行了研究，发现水滴可以悬浮的原因是：与热铁勺接触后，水滴的底部立即形成一层水蒸气，这层水蒸气可以将水与铁勺分离，因此可以使水滴悬浮，悬浮的水滴暂时不能吸收更多的能量，蒸发速度减慢，因此悬浮水滴可能在几十秒内不会蒸发，这种现象称为“莱顿弗罗斯特现象”(简称“莱氏现象”)。

莱顿弗罗斯特现象还可以推广到除水以外的其他液体，当液滴与比其沸点高很多的热表面接触时，在液滴与热表面之间会产生一层绝缘的蒸汽层，液滴不直接与热物体接触，阻止了液滴快速沸腾，液滴可以在热物体表面上悬浮。莱顿弗罗斯特现象的示意图如图1所示[1]。

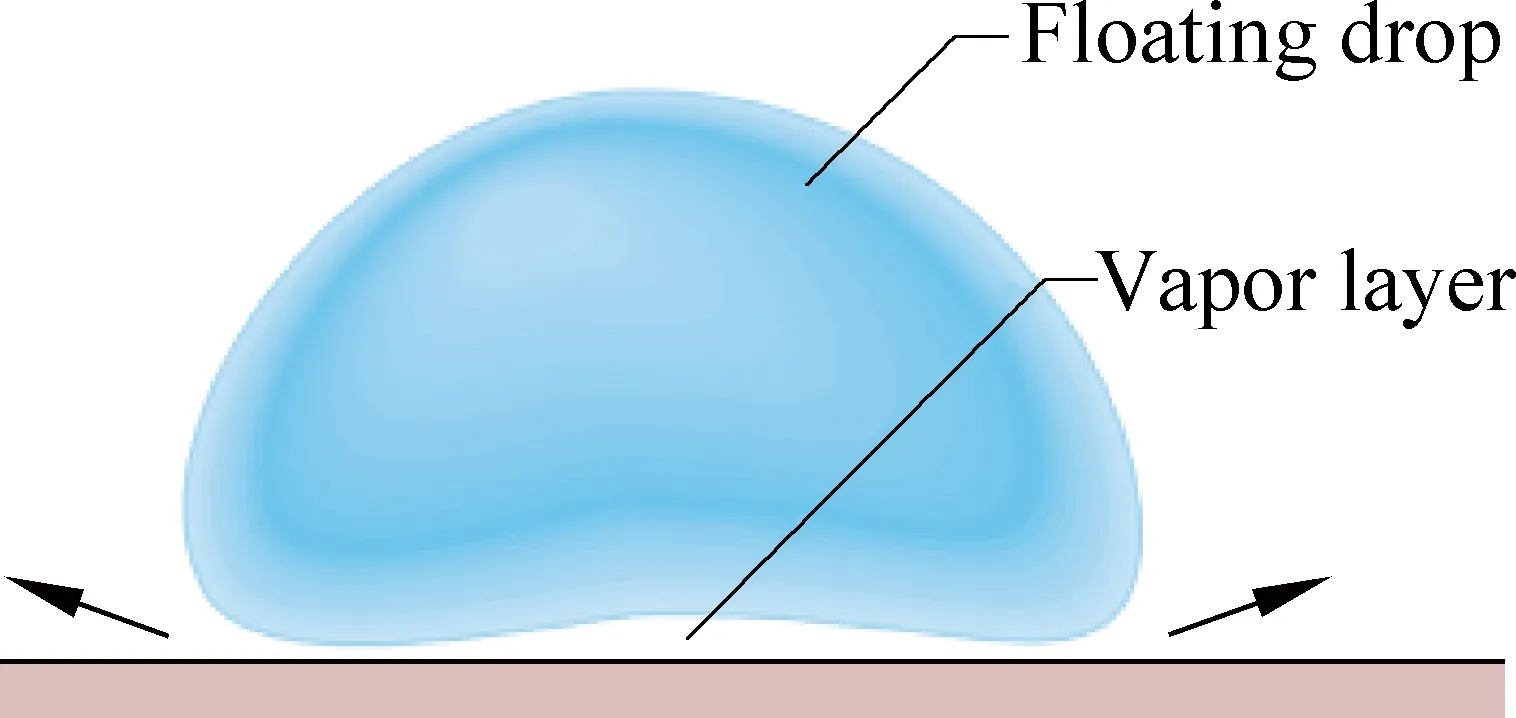
图1 莱顿弗罗斯特现象的示意图[1]

莱顿弗罗斯特通过观察进一步发现，由蒸汽层支撑的在热表面上的水滴，通过蒸汽层的传导和辐射，热量从热表面向水滴传递，水滴自发地开始振动并缓慢蒸发，振动蒸发时会形成“星形”或“多面形”的形状。莱顿弗罗斯特星的形状如图2所示[2]。

图2 莱顿弗罗斯特星的形状[2]

2 基于稳定气流法的莱氏现象实验

2.1 实验设计

在热条件下，水滴悬浮在蒸汽层上，由于热效应和水的蒸发等原因，蒸汽层的形态和动力学机制是相当复杂的，另外对于水滴体积的测量也存在困难。经学习研究有关文献发现在室温下的均匀上升气流中的悬浮液滴，在某些情况下，也可以产生振荡并形成“星形”或“多面形”，这种“星形”或“多面形”与莱顿弗罗斯特星有惊人相似之处[3，4]。为了证明莱氏现象与热效应无关，而与液滴的流体动力学机制有关，本研究设想用气流模拟液滴下方的蒸汽层，使复杂的不易把握的热效应，简化为基于流体动力学和自由表面动力学的问题，实现莱顿弗罗斯特现象，使实验成为一个纯粹的力学研究。

2.2 实验器材

鼓风机(功率535W)，高速摄像机(5000fps)，吸管束，实验水台(带有疏水金属网)，风速仪，带刻度的注射器(量程5mL)等设施。实验装置如图3所示。

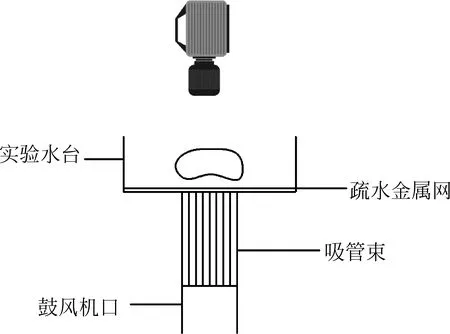
图3 稳定气流法莱氏现象实验装置图

2.3 实验操作

在实验中，将鼓风机固定好，鼓风机口朝上对准吸管束，吸管束与疏水金属网紧密连接，吸管束具有稳流消湍的作用。水台底部铺有疏水金属网，以避免液滴吸附在网格上。调节鼓风机产生一定流速的气流，控制气流通过吸管束流出。高速摄像机用来记录液滴的振荡情况。

实验中，在实验水台上滴下液滴，保持气流经吸管束，在液滴下部形成气垫。只要保持气流均匀稳定，流速大小合适，气垫可以出现并支撑液滴，使液滴悬浮振荡，实现“莱顿弗罗斯特现象”。对于固定体积(V)的液滴，其出现星形振荡的最小风速(Q)，称其为流速阈值，可借助高速摄像机和风速仪准确地测量此阈值。

2.4 实验现象

在实验中，采用固定气流流速，改变液滴体积大小的方法来进行测量阈值。观察到的现象如图4所示。

当气流流速为零时，液滴呈现稳定状态，如图4(a)所示。这种情况下，由于疏水金属网的作用，液滴的接触角一般大于 90°。

当流速逐渐增大时，液滴开始呈现无规律的振荡，如图4(b)所示。

当保持流速恒定，改变液滴体积大小，产生振荡并形成不同角数的“星形”时，如图4(d)～图4(f)。

如果流速过大或液滴的体积过大，观察到液滴破裂的现象(烟囱现象)[5]，液滴中会产生一个气泡，导致液滴破裂，如图4(c)所示。

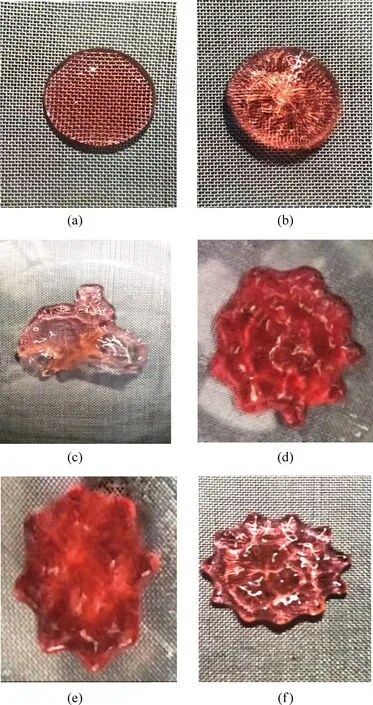
图4 实验观察的液滴形状

2.5 实验结果分析

通过多次实验发现星形振荡的角数只与液滴体积呈正相关的关系，与液滴的材料和流速无关。

为了研究液滴体积与流速阈值之间的关系，本研究采用了几组不同体积液滴，来探究其对应关系。

首先，使用水滴来进行实验。通过改变水滴体积大小和气流流速，观察水滴开始振荡的时刻，记录水滴振荡的阈值；然后使用一定浓度的乙二醇溶液(液滴的黏滞系数较大)，重复上述实验。实验结果数据如表1。

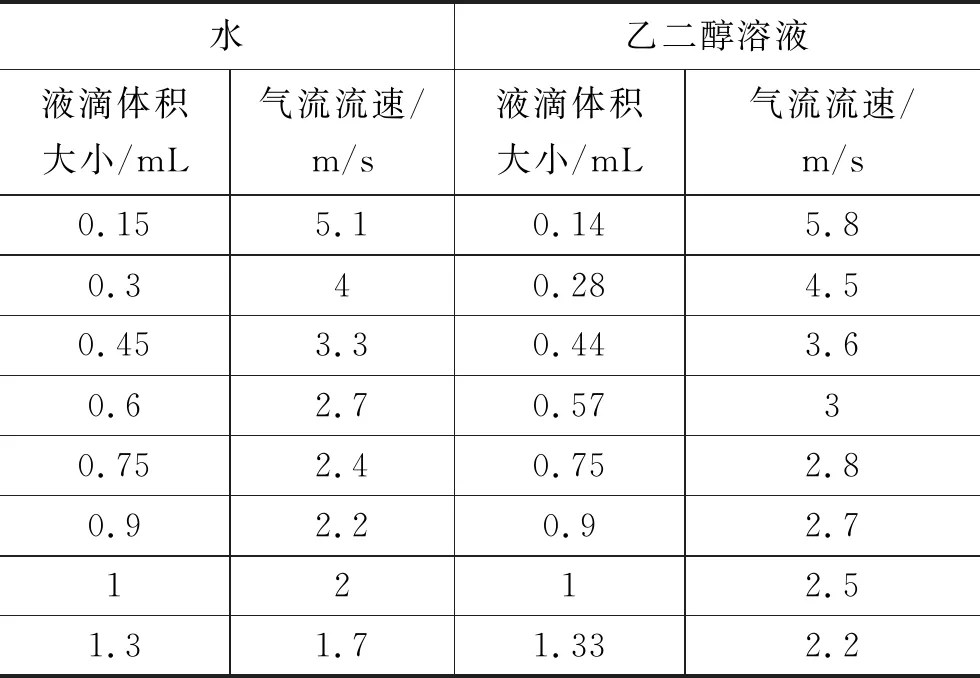
表1 水和乙二醇溶液的液滴体积和气流流速值

通过实验确定液滴振荡的阈值，实验结果如图5所示。图5中深色菱形块表示液滴体积和气流流速的关系，浅色方块表示乙二醇溶液体积和气流流速的关系。从图中可以看出，液滴体积越大，对应的流速阈值越小。左上角的两个数据点，是出现星形振荡的最大值风速，因为过大的风速会导致液滴不稳定，容易破裂，不能形成星形振荡；右下角的两个数据点是液滴体积的最大值，因为过大的体积会使液滴难以形成振荡，并且不稳定。

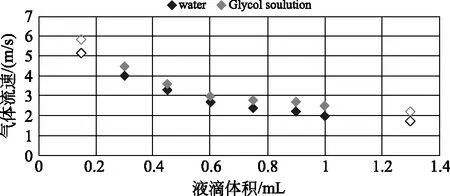
图5 水和乙二醇溶液的液滴体积大小和气流流速的关系

根据上述的实验，发现改变液滴的黏滞系数会导致流速阈值增大，然后进行了另外一组实验，实验中配置了不同浓度的乙二醇溶液(用乙二醇的体积分数表示)，乙二醇的体积分数越大，液体的黏滞系数越大。当液滴的体积为0.75mL时，实验结果如图6所示。

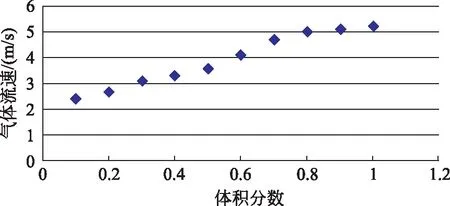
图6 不同浓度乙二醇液滴所对应的流速阈值

实验结果表明，流速阈值与液滴的黏滞系数存在正相关的关系。

3 理论与模拟

本研究通过建立一个振荡水滴的理论模型，推导出稳定振荡的理想边界条件，并运用计算机模拟的手段来证实气流条件下实现莱氏现象的可行性。

3.1 模型构建

本研究采用气液二项耦合的方式来建模，这种耦合也常被应用于模拟类似的气液交互模型(如图7)。不可压缩的液滴被假定为势流液滴，液滴下的气流为黏性气流，忽略其惯性效应。液滴的模型完全被模拟为轴对称的，目的是解释垂直振荡的出现和其驱动机制。

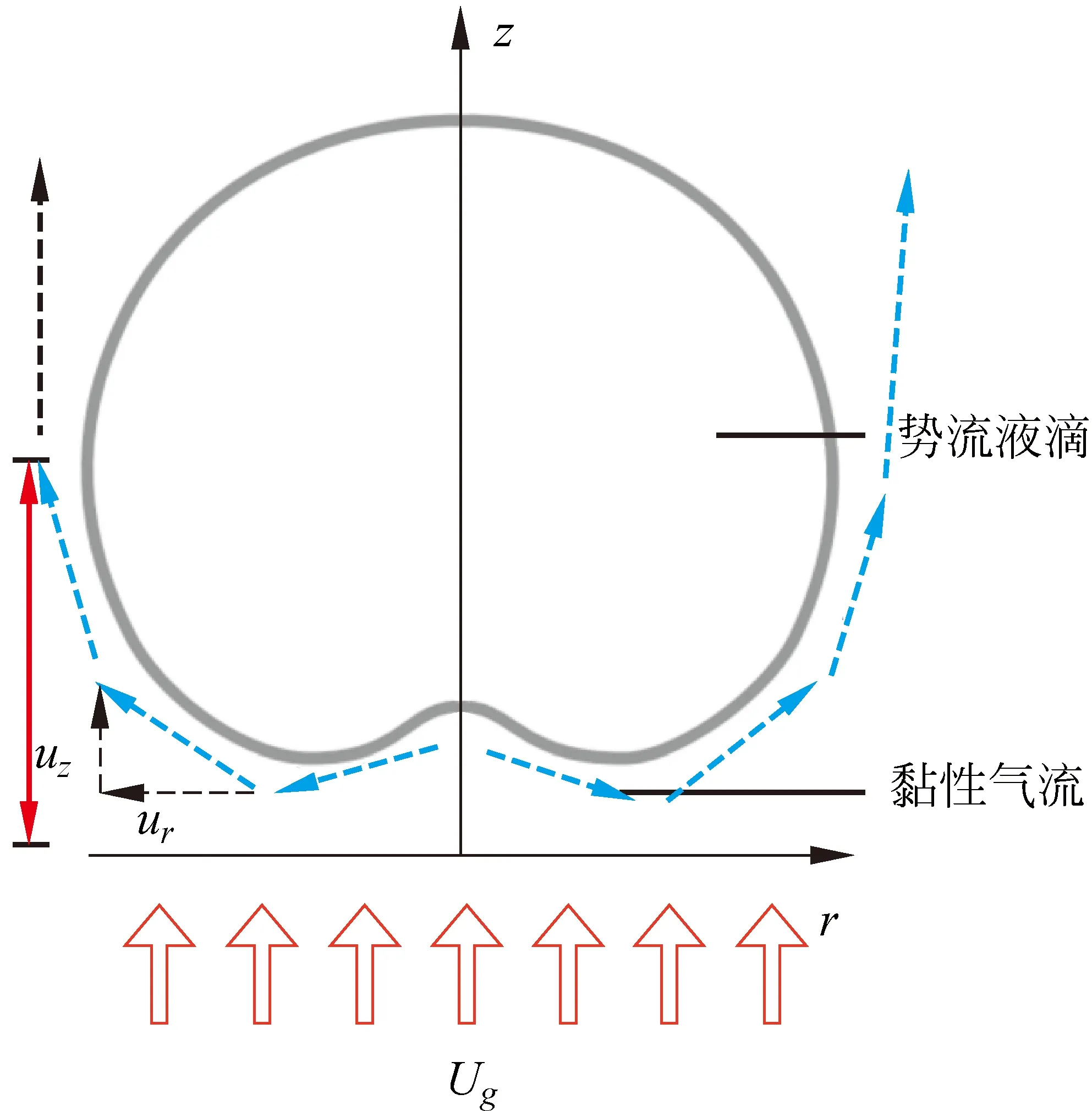
图7 气液二项耦合模型

该模型描述了一个在流速稳定的气流作用下悬浮的液滴。观察发现，液滴下方会形成一个气囊，并会周期性地释放空气，从而导致液滴的变形。图7中，虚线箭头代表的是液滴周围的扰动气流，将其分为垂直方向和水平方向来进行研究。为了排除基层网格的影响，单纯研究气流对液滴的悬浮和驱动作用，本研究建立了液滴在完全悬浮状态下的理想模型，用于解释在此实验中气流对液滴的作用原理。

3.2 理论分析

通过学习研究文献和实验探究，认为悬浮是液滴振荡的必要条件[6]，因此本研究通过理论分析，证实液滴可以在稳定气流下悬浮，并得出一种液滴悬浮的条件。

本研究首先讨论黏性气流的影响，设气体黏度为Rh。气体被定义为向上流动，具有均匀的气体流速Ca。径向气体以速度u(r，z)在液滴下部流动。为了得出轴对称润滑近似，本研究从不可压缩气流的质量守恒开始：

·u= 0

(1)

边界条件是：

(2)

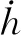
(3)

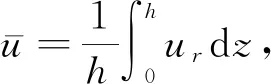
(4)

在z=0和z=h的零速度边界条件下，应用该轴对称润滑流的斯托克斯方程：

(5)

其中Pg是气体层中的压力(当管径一定时，Pg与和风速有一定的对应关系)。将其合并为

(6)

其中：

(7)

是与半径有关的空气流速。

假设液滴由不可压缩和非旋转流体组成，因此可以用势流来描述。整个液滴表面是自由表面，在适当的边界条件下，该表面的动态边界条件是不稳定的伯努利方程：

(8)

其中,t是时间;z是绝对高度;κ是液滴表面点处的局部曲率。等式左侧描述了液滴的惯性效应，Pg是在引入气流之后在液滴液面上变化的外部压力。这个方程描述了液相和气相之间的平衡状态。当整个液体-空气界面符合这个方程时，液滴进入一个稳定且完全悬浮的状态，不会与基底碰撞。在此状态下，液滴完全在气流的驱动下进行竖直、水平方向上的振动，解释了稳定气流对液滴的作用原理。

3.3 计算机模拟

在实验中，无法直接观察液滴是否与网格存在相互作用，也无法确定液滴是否能仅在气流的条件下形成振荡，因此本研究使用上述模型和理论，去掉网格，仅在气流下对液滴进行模拟。

本研究使用COMSOL(5.2版)模拟液滴的状态，采用“二相流”模型和动网格法(如图8所示)，观察液滴的运动。

图8 (a) 显示模拟中应用的轴对称模型，浅色区域代表液滴(半径2mm)，深色表示外部空气； (b) 显示应用于模型的动网格的细节

本研究先后观察了在合适的气流条件下几滴不同体积的液滴的运动，试图达到稳定悬浮的状态。而模拟结果显示了一致的现象：液滴可以保持一定时间内的悬浮振荡(如图9所示)。

这种变形的原因可以通过COMSOL模拟得到的压强分布结果来说明，如图10所示。

图10(b)显示的是顶侧压强下降，其结果是水平拉伸；图10(c)显示侧面压强下降，结果是垂直拉伸，这两种运动共同产生了振荡。本研究认为，在气流条件下实现莱氏现象是可行的。

图9 液滴位置变化的图像(t=0.001s,0.035s,0.074s,0.114s)

图10 COMSOL模拟得到的液滴的压强分布

4 结论

在实验中，本研究使用稳定气流使液滴悬浮，实现“莱顿弗罗斯特现象”，观察到角的个数在n=6～11范围内的液滴。同时，发现液滴角数只与液滴体积正相关；本研究探究了液滴体积大小、黏滞系数和流速阈值之间的关系，得出星形振荡阈值与液滴体积大小呈负相关，与液体黏滞系数呈正相关。本研究证实了星形振荡现象可以在气流条件下实现，验证了莱氏现象的产生只依赖于纯流体动力学机制，与热效应无关。