相机底片中星芒现象的研究

韩佩杉 伍泓锦 黄博文 杨浩林 贾欣燕 刘其军 常相辉 魏 云 樊代和

(物理国家级实验教学示范中心(西南交通大学)，西南交通大学物理科学与技术学院，四川 成都 611756)

1 导出问题

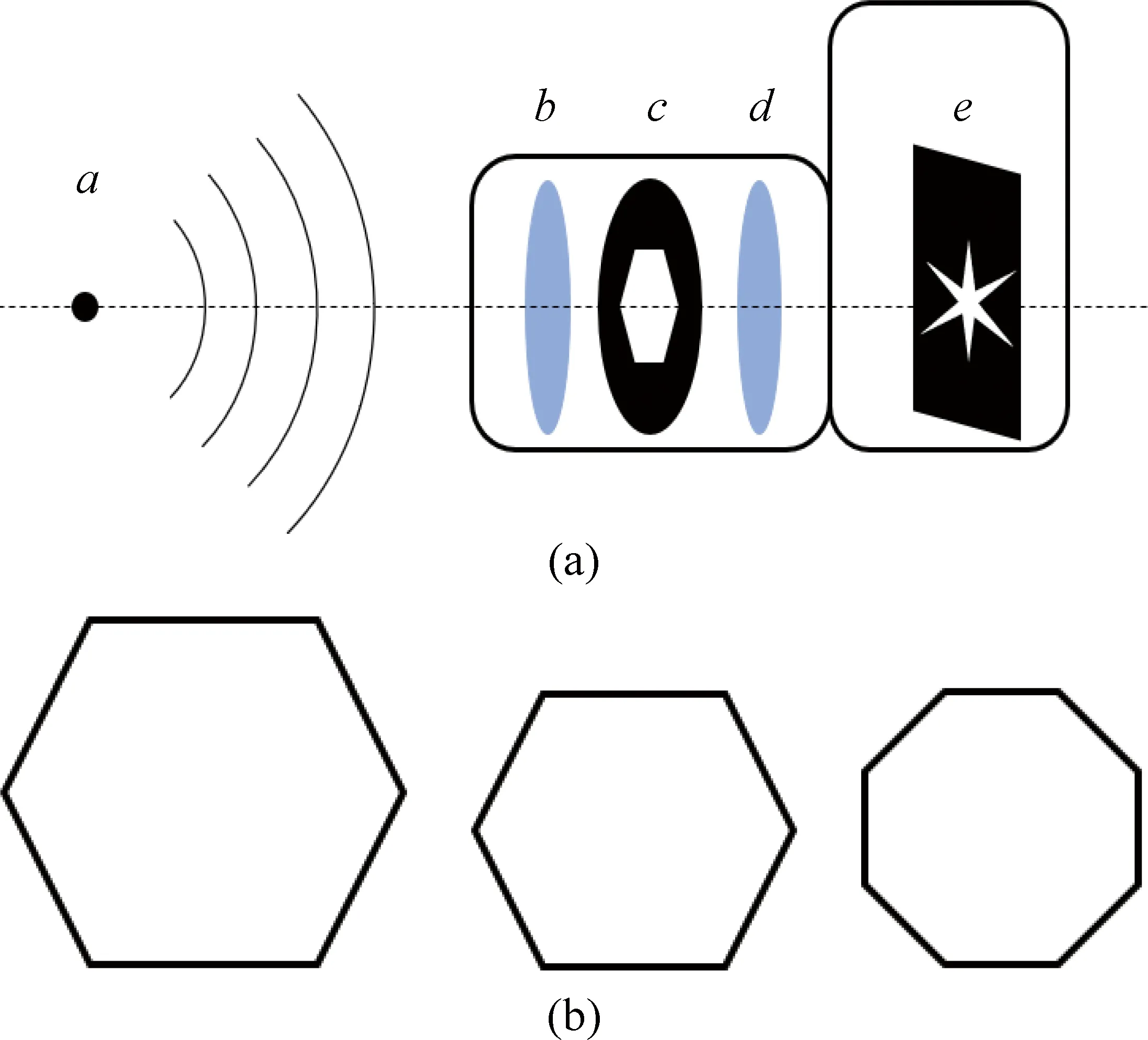
图1 相机结构示意图(a)为星芒形成示意图，a表示光源，b表示前透镜组，c表示光圈，d表示后透镜组，e表示相机底片； (b)为光圈示意图，从左到右依次为较大孔径的六叶片光圈、较小孔径的六叶片光圈、较小孔径的八叶片光圈

提灯辐射现象是个有趣的生活现象：当用相机拍摄一个发光的提灯(假设为一球状光源)时，相机底片中会显示有许多辐射状光线从提灯的中心射出，如图1(a)中相机底片上的图片所示。人们把这种现象称为提灯辐射现象，底片中围绕实际成像点射出的辐射状光线称为星芒。同时，提灯辐射现象也是2018年IYPT的一个赛题[1]，此题要求解释星芒现象的产生原因，同时研究影响星芒数量和形状的因素。

通常，相机主要由镜头部分和含有感光元件的暗箱构成。进一步，镜头部分由透镜组和光圈构成。透镜组用于将发光物体聚焦到暗箱中的底片平面，即焦平面以清晰成像[2]。光圈用于控制到达相机底片的光的强度，通常是由多个叶片组合而成的孔状结构，其形状可如图1(b)所示。组成光圈的叶片之间的开合可调节光圈的大小,叶片个数(即正多边形的边数)将影响光圈孔的形状，当叶片个数足够多时，相机光圈将接近一个真实圆形。实际上，星芒现象的出现是实际光线通过光圈结构时发生了衍射现象。

目前，光源发出的光经过小孔的衍射现象理论已经较为成熟，如杨植宗等人定性解释了光的衍射原理[3]；德国的马科斯·波恩和美国的埃米尔·沃尔夫定量解释了光通过不同形状孔的衍射情况[4]；姚启钧解释了光的衍射现象并得出在夫琅禾费衍射区内的衍射积分公式的一般形式[5]；戴又善研究了正n边形小孔夫琅禾费衍射光强分布[6]等。通过这些现有理论结果可判断，相机底片中星芒现象的出现与光通过相机中非圆形孔状结构的光圈后产生的衍射现象有关。然而，现有针对衍射现象的理论研究大都是探讨星芒个数与孔的边数的关系，同时对星芒细锐度影响因素的探究尚不够全面，特别是实际相机成像中星芒现象出现的具体原因，以及相关参数对其的影响还未见报道。

本文主要分析实际光线通过光圈后的成像，将实际问题转化为简单的物理模型，利用光的衍射理论，结合数值模拟分析，从理论上彻底解释了星芒现象出现的原因，以及相关因素对星芒个数及细锐度的影响。进一步，本文使用具有不同叶片数和不同孔径大小光圈的相机对发光物体进行了拍照实验，利用软件分析了相机底片中星芒的个数及细锐度等参数，实验结果与理论模拟一致。

2 理论分析

提灯主要由中心光源和周围玻璃构成，当相机距离提灯足够远进行拍照时，其可以看作一个点光源。根据相机的成像原理[7]，整个相机成像过程可由图1(a)所示的物理模型进行分析。假设光源发出波长为λ的光，先后经过前透镜组b、光圈c、后透镜组d后交于相机底片e上，最后分析底片上衍射光的光强分布即可对星芒现象进行研究。由于光源距离镜头很远，入射光可以近似为平行光。

对如图1(b)所示的实际相机中的光圈而言，其实际为一个正n边形孔，此孔可看为是由n个等腰三角形孔组成，假设每个等腰三角形的底边长为L，高为h，三角形内任一平行于底边的线长为l，如图2所示。

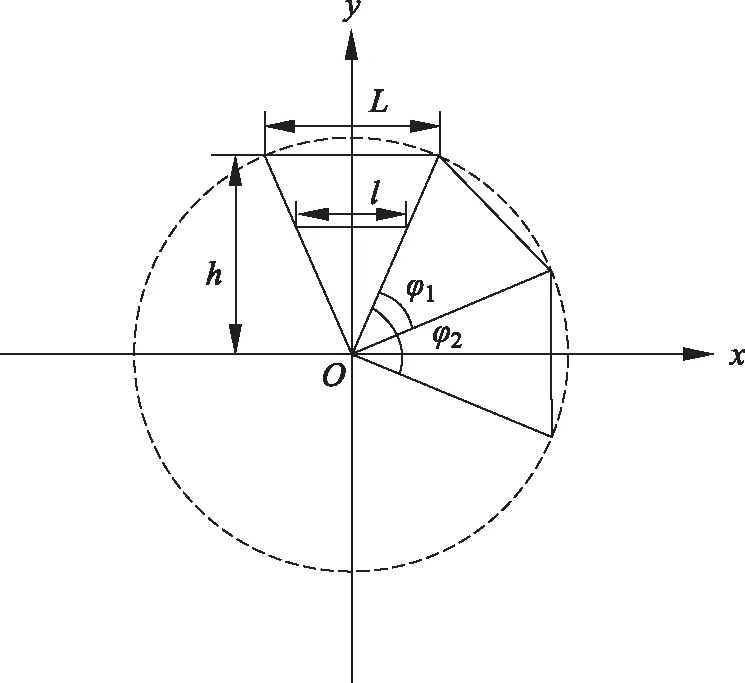
图2 正n边形光圈的等效等腰三角形孔示意图

根据菲涅耳直边衍射分析[8，9]可知，光通过相机的光圈时，会在每个叶片(即正多边形底边)上产生一束垂直于传播方向的衍射峰，投影到相机底片上时整体显现出由中心向外发射的星芒现象。当光源距离相机光圈较远时，由于傍轴近似，光源可以看作点光源，其发出的光经前透镜组准直，可以近似获得平面波，菲涅耳衍射近似为夫琅禾费衍射。另外，菲涅耳衍射需要使用复杂的积分，计算量大，难以得到准确的解析解。而夫琅禾费衍射通过简单的计算即可得到比较精确的衍射光强分布。因此要研究光通过一个正n边形光圈的衍射情况，只需要分别求出光通过n个小三角形的衍射场复振幅分布，最终将所有小三角形衍射场复振幅分布叠加即可[10，11]。

图3 不同边数孔的衍射光强二维分布图 (a) 正三角形孔； (b) 正四边形孔； (c) 正六边形孔； (d) 正七边形孔； (e) 正八边形孔； (f) 正十四边形孔

平行光通过如图2所示的最上面的一个三角形孔后光波的复振幅分布可写为[6]

(1)

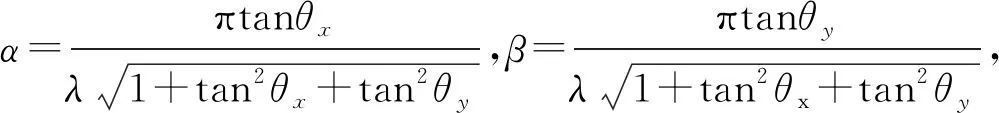
(2)

将式(2)代入式(1)可以得到转动φk后的等腰三角形小孔的衍射光波复振幅分布表达式：

(3)

若将n个小三角形孔看作n个同顶点的全同孔组成的阵列，则通过正n边形孔的光波复振幅分布为所有等腰三角形的复振幅叠加[10]：

(4)

因此，当平行光通过一个正n边形孔组成的光圈后，相机底片中所成像的光强分布可写为

I(n)=|E(n)|2

(5)

结合式(4)、(5)可以看出，相机底片上的任一点的相对光强大小与n值和L值有关，其中n值代表相机光圈的叶片数；L值决定了光圈大小，可通过调节相机设置中的光圈大小值来改变。为了更明显看出其相应关系，我们可以引入傅里叶光学中的夫琅禾费衍射公式，代入二维三角函数的傅里叶变换，得出通过一个三角形孔的光波在观察平面上的复振幅分布[13]：

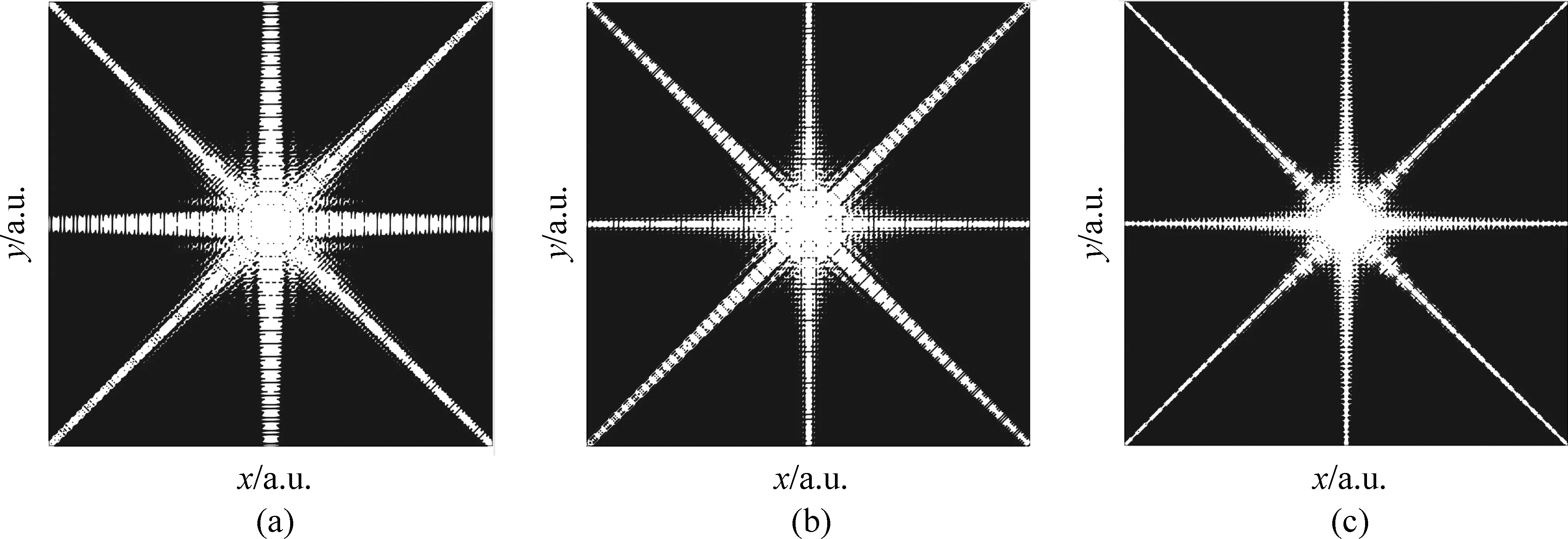
图4 不同孔径大小的衍射光强分布图(a) L=0.005m； (b) L=0.004m； (c)L=0.003m

(6)

由于最终结果仍较为复杂，我们采用Mathematica软件进行数值仿真模拟以增加可观性。

首先，通过仅改变n值，保持多边形孔外径不变，模拟叶片数对星芒的影响。仿真时，取正多边形孔的外径为0.006m，波长选取为λ=400nm，可以得到相机底片中所成像的强度二维分布图，结果如图3所示。

图3中，从(a)到(f)，分别表示当光圈结构分别为正三、四、六、七、八、十四边形(即n=3、4、6、7、8、14)时得到的二维强度分布图。从图3(a)到图3(f)中可以看出：星芒出现的个数分别为：6、4、6、14、8、14条。由此可得知，构成相机光圈的叶片数在上述范围时，出现星芒个数与叶片数之间的关系为：当相机光圈为中心对称图形时，出现的星芒个数为叶片数；当相机光圈为轴对称而非中心对称图形时，星芒个数为叶片数的二倍。我们同时模拟了更多不同n值对应的仿真图像，均得到了如上相同的结论。对该现象进行定性分析可知，光线在通过光圈时，在每个叶片上都产生一对垂直于叶片方向的星芒。偶数个叶片的光圈为中心对称图形，对边上产生的星芒方向重合，因此n个偶数叶片将形成n条星芒；对于奇数边的情况，光圈为轴对称而非中心对称图形,每个叶片上产生的星芒方向都不相同,因此n个叶片将形成2n个星芒。实际上，我们模拟了当n=50时的多边形孔(近似于圆孔)，星芒现象将接近消失，即多边形孔衍射趋近于圆孔衍射。

其次，当保持相机光圈叶片个数为8，即n=8，改变L值(即改变光圈孔径大小)，数值模拟得到了入射光通过光圈后的二维光强分布图，结果如图4所示。

从图4可以直观地看出，当光圈的边长从0.005m变到0.003m时，单条星芒的宽度将越来越细。因此，可以认为，光圈孔径大小将影响出现的星芒的细锐度：当光圈的孔径越小时，星芒将越细锐，即衍射效果愈明显，完全符合夫琅禾费衍射特点。

3 实验研究

为了验证以上数值模拟结果，在距离镜头较远情况下，将普通节能灯近似为点光源，选取同种型号但具有不同叶片数的镜头进行实验研究。为了减少环境光对实验结果的影响，整个实验在完全黑暗的环境下进行。实验时，将一节能灯固定在实验室走廊的一端，将相机固定在距离节能灯约10m远的三脚架上，并保持镜头和灯泡正对且等高，最后通过相机拍摄了若干不同条件下的照片。

首先，保持相机光圈大小不变，研究了光圈叶片的个数对星芒个数的影响。我们以光圈大小F22为固定值，曝光时间固定为10s，焦距为150mm，分别更换光圈叶片数为6、7、8的镜头对光源进行了拍摄，拍摄得到的成像图最终转换为一700×700像素的灰度图像，如图5所示。

从图5可以看出，当选用光圈的叶片数分别为6、7、8时，出现星芒的个数分别为6、14、8，实验结果与上述数值模拟规律一致。受实验室现有镜头组条件所限，没有进行更少或更多叶片数的实验研究。

其次，保持叶片个数不变，探究了光圈大小对出现的星芒细锐度的影响。选用光圈叶片数为8的镜头，固定曝光时间为10s，焦距为150mm，改变光圈大小分别为F16、F18、F22。由于F=镜头的焦距/镜头光圈的直径，因此对应的正八边形光圈的实际边长分别为3.6mm、3.2mm、2.6mm。最终得到的图像如图6所示。

图6 叶片数为8时，改变不同光圈大小的拍摄图像(a) 光圈大小为F16； (b) 光圈大小为F18； (c) 光圈大小为F22。其中横向白色的水平线表示纵向700像素中，第200像素所在的位置

从图6中可以看出，随着相机光圈边长的减小，出现的星芒的细锐度越高。为了更直观地数值分析图6中出现的星芒的细锐度，我们利用LabVIEW软件分析了图6三幅图中，纵向坐标在第200处(如图中的浅灰线所示)的水平线的归一化灰度图，结果如图7所示。通过比较最中间星芒所占的像素范围的大小(范围越小，说明细锐度越高)，即可直接分析星芒的细锐度。

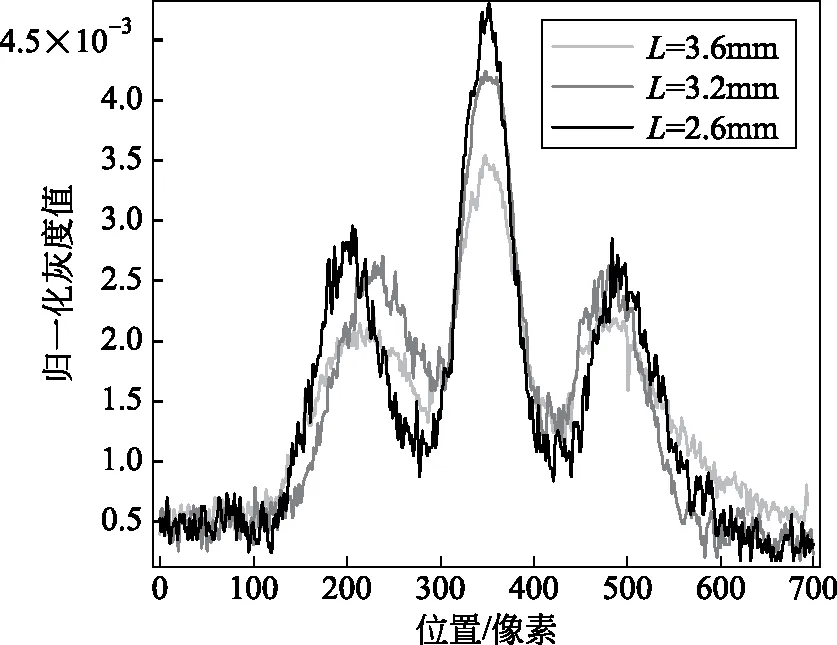
图7 纵向坐标为200像素点的横向归一化灰度图(图6中浅灰线位置)

图7中，每条曲线的3个峰分别表示了图6中每张图浅灰色横线所在位置出现3个峰，直接比较最中间峰所占用的像素值范围即可得知细锐度的大小。可以看出，随着光圈F值越大，即光圈的实际孔径越小(L越小)，峰中心光强越大，同时对应的像素范围也越小，表明形成的星芒将越细锐。该实验结果与理论分析基本一致。事实上，我们也分别用六叶片和七叶片的相机镜头进行了类似的探究细锐度的实验，均得到了相同的规律。

4 总结与讨论

本文从理论和实验两方面对星芒现象进行了研究。首先从理论上给出了平行光通过不同形状和大小的孔后的光强分布表达式，并用Mathematica软件数值仿真模拟了不同条件下星芒现象的特征，得出了光圈叶片数与星芒个数的关系为：当相机光圈为中心对称的正多边形时，出现的星芒个数为叶片数；当相机光圈为轴对称而非中心对称的正多边形时，星芒个数为叶片数的二倍。同时，数值模拟结果得出：镜头光圈孔边长越小，星芒将越细锐。进一步，本文对星芒现象也进行了实验研究。通过利用具有不同光圈结构的相机对实际光源进行拍照，分析了相机底片中出现的星芒数量和细锐度等问题，实验结果与理论结论一致。本文也较为完美地解决了2018年IYPT赛题之一中提到的提灯辐射问题。