简化弹道设计方法在运载火箭型号论证中的应用

张博俊,王俊峰,李大鹏,肖 清

(北京宇航系统工程研究所,北京 100076)

运载火箭弹道设计是一种典型的非线性规划问题,由于火箭的构型不同、目标约束不同,往往需要根据火箭构型进行多个控制变量的优化,计算工作量大。在运载火箭构型论证阶段,需要根据可能的轨道、构型、发动机种类、加注质量进行组合,并在其中找到一个运载能力最大的构型,工作量非常大。同时,由于构型不同,火箭的控制变量也不尽相同,难以进行统一建模,往往需要根据具体轨道、构型进行精细设计才能得到最优运载能力。因此,有必要针对运载火箭弹道设计问题进行分析、简化,构建一种通用的、易于寻优的简化弹道设计方法,满足减少运载火箭构型论证工作计算量的需求。

张子明等[1]探讨了运载火箭上升段的主要优化参数。张柳等[2]在此基础上提出了一种基于PSO-Powell算法的运载火箭优化算法,认为影响火箭运载能力的主要变量为各级程序角。胡冬生等[3]分析了不同约束变量对火箭运载能力的影响。洪蓓等[4]提出了在有入轨约束的情况下进行运载火箭弹道优化的算法。熊伟等[5]提出了一种利用遗传算法和牛顿迭代法共同对弹道参数进行寻优的方案。这些方案都提出了一系列针对固定构型的运载火箭弹道优化思路。本文根据对多种构型火箭不同发射轨道的研究,提出了一种简化弹道设计方法,解决在构型论证工作中运载火箭的运载能力优化问题,极大地减少了计算量。该方法通过简化入轨级程序角设计方法使不确定的非线性规划问题转化为一次牛顿迭代寻优过程,提高了计算效率。通过对国内外的2种运载火箭的飞行曲线拟合,验证了该方法的可行性和正确性,证明了简化弹道设计方法可以满足构型论证工作中由于轨道、构型不确定产生的统一弹道计算方法的需求。

1 弹道计算的数学模型

1.1 动力学模型

建立在发射坐标系下的火箭的上升段弹道三自由度质点动力学方程[6]:

(1)

(2)

(3)

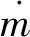
1.2 飞行程序角模型

在文献[2]的基础上对飞行程序角进行一定的修改,公式分为3部分,其中前两部分全称为重力转弯段,该段的飞行程序如下:

(4)

式中:α为攻角,θ为弹道倾角,ωz为地球旋转角速度在发射坐标系z轴方向的分量,tturn为垂直段飞行时间,则

α=4αMetturn-t(etturn-t-1)

(5)

式中:αM为常量,也是迭代参数。

根据式(4)、式(5)可以得知,火箭的重力转弯段分为2个过程,一个是从t0到tturn的垂直起飞过程,该时间可以由火箭出发射塔时间计算得出;另一个是重力转弯过程,在这一阶段,攻角α的曲线由期望的关机点程序角终值迭代αM得出,并最终计算得出飞行程序角。

转弯段关机后至停泊轨道为第3个部分,该段程序角为

(6)

(7)

1.3 推力启动段关机段的简化

在实际火箭飞行过程中,必须考虑到火箭每一级发动机启动段的推力、流量的建立、关机过程,情况较为复杂。同时,由于冷热分离情况不同,因此在实际的火箭弹道计算过程中,发动机推力的建立和关机是必须详细考虑的。另一方面,推力、流量的曲线并非线性变化的,不同推进剂的发动机的启动、关闭时间也不相同,因此很难用一个框架来统一化处理。

经过大量分析,由于发动机启动、关闭阶段的总时间较短,提供的总冲量相对于整个飞行过程来说极小,因此可以直接将这一部分略过,认为这一部分的流程直接可以产生标称的推力,不计算启动关机过程,改为由节流时间和节流程度来模拟启动、关机过程。

因此,推力公式可以改写为

(8)

(9)

2 迭代模型的通用化处理

在构型论证阶段,由于火箭构型未定,因此在进行设计的时候很难固定参考某一在飞型号进行弹道优化设计,因此有必要针对优化算法进行通用化处理,使程序能够适应大多数在飞、在研的火箭构型。

2.1 火箭弹道设计模式

目前在飞的火箭构型主要有以下几种:

①光杆构型。无助推,可能有两级火箭或者三级火箭。

②助推构型。有助推,可能有两级火箭或者三级火箭,各芯级关机时间有可能与助推相同或者延后。

③火箭加上面级状态。在上述2种火箭的基础上加上上面级,由上面级带卫星直接入轨。

而入轨的轨道有以下几种:

①直接入轨型太阳同步轨道(sun-synchronous orbit,SSO)、近地球轨道(low earth orbit,LEO),无滑行状态,火箭直接进入目标轨道;

②霍曼转移入轨,需要在基础级或者一级/二级飞行完成后,由入轨级滑行一段时间到达原地点后点火进行轨道圆化。

可见,经过排列组合后,构型论证需要面对的工况数量庞大,而且难以固定一种设计方法进行弹道计算。因此有必要针对这种情况进行统一的弹道设计方法建模,适应不同的情况。

2.2 弹道整体分段

一般来说,可以认为霍曼转移入轨是在火箭进入一个稍小的圆形或者椭圆轨道后,再滑行一段时间到指定位置,发动机二次启动进入目标轨道的过程[8]。很明显,在第一步的弹道设计中,设计过程是相同的。因此,在这里将计算流程整体分为2种状态:非滑行状态和滑行状态。非滑行状态是指火箭直接入轨各种轨道;滑行状态是指在非滑行入轨后,再增加滑行段和最终入轨段。

由于目前的火箭动力水平达不到单级入轨,直接入轨弹道至少需要两级才能入轨,所以,可以设计第一段弹道为重力转弯弹道,后续段为入轨弹道。

重力转弯弹道在文献[9]中有具体的设计方法描述,在这里不再展开。重力转弯后,一般助推或一级将进行分离,而为了提高运载能力,一级/二级等将会多飞一段时间,这一段的工作级的数量是不一定的,有可能是单二级工作(Falcon9),也有可能是一级、二级一起工作(CZ-7)或者一级、二级、三级一起工作(CZ-3B)。各类火箭的构型不同,弹道设计时的设计变量也不相同,因此不能以火箭工作级作为俯仰程序角的设计分段。

针对这种情况,可以将火箭第一次关机作为重力转弯段终止点,将后续直到入轨的各段统一作为一段真空推力段来进行设计,并将这一段称为入轨段。这样,可以将重力转弯段后未知的火箭级数统一起来,认为是由一个程序角变化率和对应的飞行时间控制的飞行段。该段的主要任务是控制火箭从重力转弯段后到入轨的这一段的飞行轨迹。

2.3 非滑行状态设计方法

在实际弹道设计过程中,首先估计一个转弯段俯仰程序角终值φ0,这样就决定了本次计算时入轨段的起点,然后使用入轨段的3个控制参数进行迭代设计达到入轨要求,流程如下。

(10)

(11)

解完方程组后,即可得到能够满足从转弯段终点到入轨点的一组控制变量。

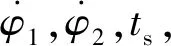
图1 不同φ0对后续程序角的影响

运载能力曲线如图2所示,图中,mt为载荷质量运载能力。由图2可见,不同的φ0对应的运载能力是一条反抛物线,可以解出极值。

图2 不同φ0对应的最优运载能力

可见,在不同的重力转弯段程序角终值φ0的情况下,运载能力明显成反抛物线型,因此可以使用牛顿迭代算法对φ0进行寻优,即可找到最优运载能力。

2.4 滑行状态

针对上面级入轨或霍曼转移入轨计算时,可以将2.3节计算完的最优停泊轨道作为计算的初始状态,并增加一段无动力滑行段和一段动力段,实现运载火箭从停泊轨道到目标轨道的转移。一般来说,仅需要进行一次工作就可以满足入轨要求,因此设计思路更加简化。

③重复计算至满足入轨要求。

这样就可以在原本的停泊轨道的基础上,计算出SSO或GTO轨道的运载能力,完成了构型论证的验证。

综上所述,通过分析非滑行入轨和滑行入轨的2类轨道设计流程及不同火箭构型的设计思路,将非滑行入轨弹道设计抽象为2段入轨设计思路,对设计流程进行了简化。将复杂的、不确定非线性规划问题简化为对转弯段程序角φ0的梯度寻优过程,极大地简化了弹道设计的复杂度。

3 模型验证

为验证简化模型在不同构型火箭、不同发射任务中的应用效果,选取了美国SpaceX公司的Falcon9火箭发射铱星任务和典型CZ-3B火箭发射任务进行复算。

3.1 CZ-3B改进型火箭

使用简化模型后,计算长三甲系列火箭用户手册中的典型CZ-3B火箭任务轨道参数,计算运载能力结果为5 510 kg,手册中给出的运载能力为5 500 kg,二者极为接近。表1对比了手册及简化弹道设计方法计算出的主要动作时序。由于CZ-3B火箭一级、二级属于热分离,因此时间偏差较小,到三级第一次关机后,由于简化模型未计算后效等方面的影响,累计了一些时间偏差,但启动段、关机段冲量较小,未对运载能力产生较大影响。

表1 CZ-3B典型任务时序对比

图3显示了简化弹道设计方法计算出的运载火箭速度、高度曲线与CZ-3B典型发射任务的速度、高度曲线的对比情况,由图可见,二者十分接近。

图3 CZ-3B速度、高度对比曲线

图4为使用简化弹道设计方法后计算得出的CZ-3B火箭飞行程序角。

3.2 Falcon9火箭

Falcon9火箭参数来自SpaceX官网,根据发射任务手册,本次Falcon9火箭发射任务载荷为9.6 t,使用简化弹道设计方法计算后,得到运载能力为9.69 t,二者差距较小,一级、二级主要动作时序见表2。由表2可见,由于参数资料较少,实际飞行时间有一定的偏差,但各分段时间差异不大。

表2给出了Falcon9铱星任务实测飞行时序与拟合弹道的对比情况。

表2 Falcon9铱星任务时序对比

图5给出了简化弹道设计方法计算出的Falcon9铱星任务的速度、高度曲线,并与该任务视频中给出的速度、高度曲线进行了对比。由图可见,通过简化弹道设计方法计算得出的拟合弹道与实际飞行数据贴近,拟合效果较好。

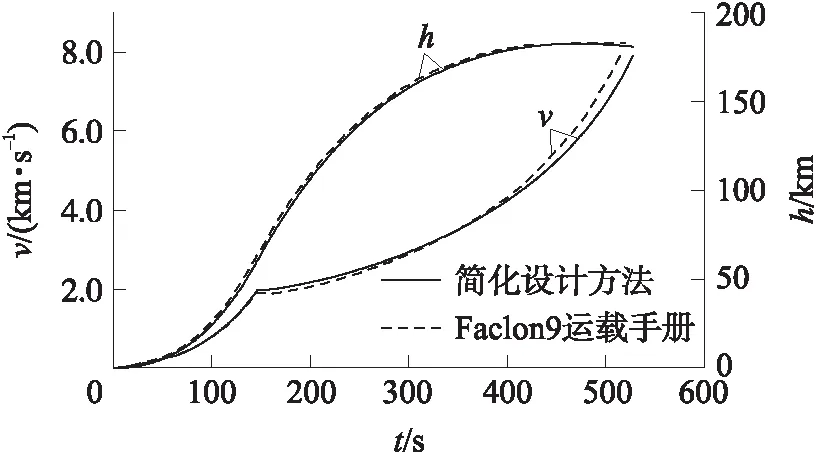
图5 Faclon9速度、高度对比曲线

图6中给出了Falcon9铱星任务使用简化弹道计算方法得出的飞行程序角。

图6 Falcon9铱星任务飞行程序角曲线

由CZ-3B、Falcon9 2种构型的火箭运载能力计算、实测数据比对可以看出,简化弹道模型通过较少的输入参数、更简单的控制变量和计算方法即可达到很高精度的弹道复现,证明了简化弹道设计方法的可行性。

4 结论

通过理论分析,本文对现有的弹道计算模型进行了简化,极大地减少了输入数据的类型和数量,并将不确定的非线性弹道设计问题简化为梯度寻优过程。使用简化弹道设计方法对CZ-3B、Falcon9 2种构型完全不同的现役运载火箭的实际飞行曲线进行了拟合,对比结果显示,尽管存在一定的偏差,但整体上曲线复现效果较好,运载能力接近,证明了简化弹道设计方法的可行性、正确性。因此,可以认为简化弹道设计方法可用于构型论证阶段的弹道计算。