初中数学“认识封闭”突破策略研究*

☉江苏省泰兴市黄桥初级中学 徐新燕

☉江苏省泰兴市西城初级中学 周小峰

认识封闭现象的存在，已经有不少人对其视而不见，但实际上，认识封闭现象对于数学学科的教学和学习带来一定的警示意义.“把不会当成不能”“对认识封闭现象的忽视”等，都是当前数学教学工作者和研究者需要解决的困境.无论是对一个问题或者技术的不会，还是将其视为自身能力有限，对于数学教学来讲，都需要全面认知，并找到认识封闭现象的认知方法和体系.

一、认识封闭现象的含义

所谓认识封闭现象，主要指针对一个问题，当事者是可以理解并且认知的，但是要解决这样的问题难以使用已有的知识和理论来突破，由此形成一个认识到实践的转化困境，这个过程被称为认识封闭现象.在认识封闭概念中，不是说能解决或者会解决，而是不具备解决问题的一些必要条件.对于问题解决的办法，从问题原因剖析的层面看，有许多角度的因素限制.在讨论为何会出现认识封闭现象时，我们有必要关注解答问题和解决问题当事人是否具备解决这个问题需要的方法论或者技巧.

主体没有把握相关数学知识的本质属性是导致认识封闭的主要原因.数学方法论或者问题都有对应的知识理论，如果没有把握这个适应的范围，就不能将正确的数学知识应用于对应正确的问题实践中.所以要科学把握数学知识的适应范围极为关键，这和数学问题实质性理解和数学问题认识深度有一定联系.此外，个体缺乏科学研究的精神是比与个体对数学知识的认知深度有关造成“认识封闭”更严重的现象，如果不能对一个知识适用的实践领域有可靠的证据证明，那么就不能给出成功的反驳例子.

二、教师的认识封闭现象

当数学教师为学生评价问题解答的状况时，需要判定是否存在认识封闭现象.避免因为教师的认识封闭导致学生正确的解答遭到误解，由此无形中对学生的学习成果产生误判，进而影响学生对学科的学习积极性.当学生在解答一个相对困难的题目时，若利用自身学习的知识不能解答，这就需要数学教师从自身去寻找原因，是否在题目设计和布置方面欠缺思考，找到产生认识封闭问题的原因.如例1中，题中条件的严谨程度导致了“认识封闭”现象的产生.

例1有长为32米的栅栏，想要利用一面墙来围成一个矩形草坪，若墙的长度不限，设AB=x，当AB为多少米时，草坪的面积最大？是多少？

所以当AB=16时，面积最大，为128平方米.

变式训练时，教师提出若墙的长度为10米，其他条件不变，草坪面积最大为多少？那么当x=10时，面积最大，为110平方米.

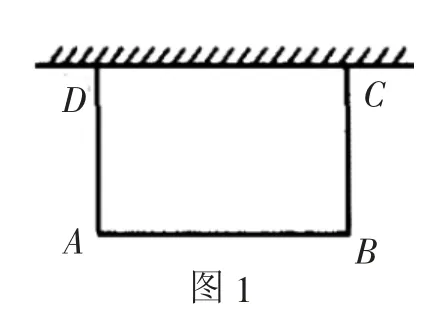
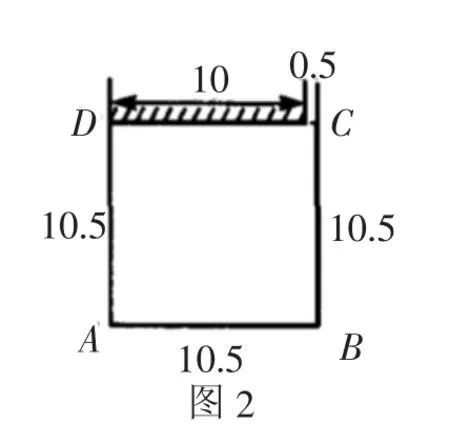
从二次函数角度看，解题思路完全没有问题，但是条件“利用墙”并没有规定其中一边只能为10，还可以如图2所示围成草坪，那么这样草坪的面积就变成110.25，比110大，若题中条件改为靠一面墙围草坪，就只有第一种情况了.出现这样的现象在于条件的给出不严谨，若学生在解题过程中，思考较多想到了这一点，而教师却误判，那么就会产生认识封闭现象.

数学本身就是一个严谨的学科，站在学生的角度思考认识封闭现象，教师应当避免这一现象给学生学习数学知识和解决数学问题造成不利影响，进而影响学生的身心健康和是非辨别能力.

认识封闭现象和认识通畅现象是相互对立的.但是不能认为有了认识通畅就能成功抵抗认识封闭，因为无论是否陷入认识封闭境地，都需要当事者对解决问题所需要的知识理论和概念进行重新的、全面的认知.当对知识和理论有了实质上的掌握后，才能获得打通认识封闭通道的根本办法.数学学科有自身适应的对象范围，也包括不适应的，所以，应当以辨证的视角和方法来探究认识封闭和认识畅通，这样才能从本质上解决问题.要辨证看待认识封闭现象，需要教学者跳出较低的视角范围，因为认识封闭现象实际上和认识通畅现象有着一定的认识联系，教学工作者可以通过正、反两方面的例子来研究认识封闭现象，避免在重复循环的认识模式中再次陷入认识封闭境地.

三、学生的认识封闭现象

“把不能当能”和“把能当不能”是认识封闭现象产生的主要体现.其中，前者主要指的是对一个知识理论的错误认识导致当事者认为能够利用这一知识解决问题的错误倾向；后者则是指本来可以使用一种知识或者理论解决现实问题的，但事实上并没有使用这一知识.

1.“把不能当能”

概念是任何一门知识学科的基础内容，也是整个知识体系得到有效结合的根本.数学学科也是由多个概念连接的有机体系.各类概念、符号、公式都是构成数学学科的主要部分.因此，每个组成部分都有其自身的逻辑特征.因此，在解题时，学生需要弄清楚每个题目中各个概念、公式之间的联系，厘清概念间的关系才能成功解题.但是关于认识封闭，也有一方面原因来自于思维错误，也就是对数学符号、公式等概念的理解错误导致.

例2图3是一个几何体的主视图及左视图，该几何体是由n个完全相同的正方体组成的，请问：正方体个数是几？

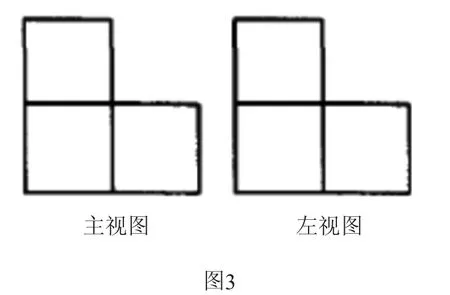
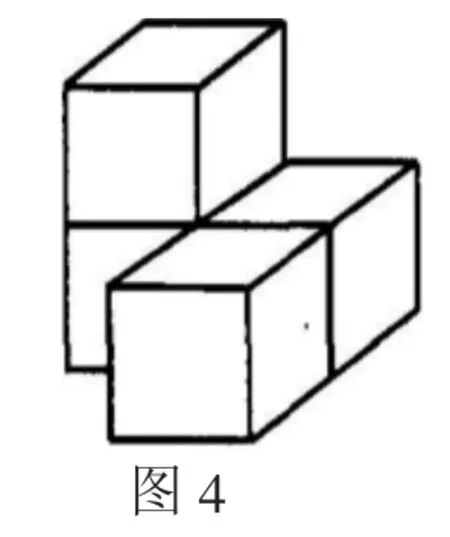
大部分学生的答案都如图4、图5所示，但也有少数学生给出了图6中所示几何体.这道例题不仅考查三视图相关知识点，还考查几何体的相关概念及性质，也就是说图6算不算一个几何体.根据运动的观点来看，面动得体，因此至少有一个面是几何体的公共面，还有内部需要具有空间连通性，图6是由两个几何体组合而成的，并不算作几何体.此题中将一个不能称为几何体的图形称为几何体，脱离几何体定义，“将不能当能”也是认识封闭的一种.由于数学公式或者概念认知误区的出现导致对实践应用范围的认识错误，这也是许多学生认识封闭的一种原因.

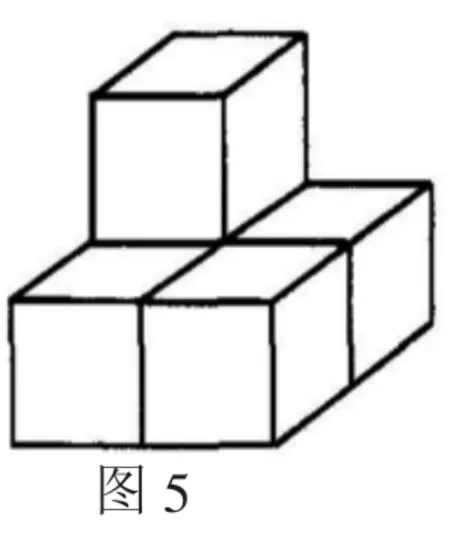
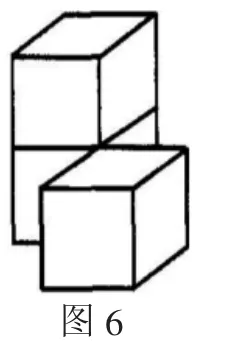
2.“把能当不能”

例3某花圃发现盆栽价格与盆栽中花株数有关，每盆植入3株时，平均单株盈利3元，以同样的栽培条件，若每盆增加1株，平均单株盈利就减少0.5元，要使每盆的盈利达到10元，每盆应该植多少株？

教师让学生A与B上黑板演示做题过程.

学生A：设每盆花增加x株，则每盆花有（x+3）株，每株盈利（3-0.5x）元，所以（x+3）（3-0.5x）=10，得x=1或x=2，所以每盆植入4或5株.

学生B：设每盆花应植入x株，则9+（x-3）（3-0.5x）=10，得x=4或x=5.

这时有些学生就会认为学生B是错误的，这就产生了“把能当做不能”的认识封闭现象.他们认为方程9+（x-3）（3-0.5x）=10中（x-3）与（3-0.5x）中的x含义不同，（x-3）中的x表示的是每盆应植入的株数，而（3-0.5x）中的x表示的是每盆应增加的株数，这是因为学生A的答案造成的定式思维，认为（3-0.5x）就应该表示单株花的平均盈利，但学生B的方程中（3-0.5x）其实表示的是增加盈利平均到增加的x-3 株花的单株花的平均盈利，若式子列成学生就易理解了.

作为教师，应当注重认识封闭对学生学习带来的不良影响.但是最终提醒我们的是，当前的考试模式已经不再适用新时代的教学需要.在学习成果的检验中，我们基本上都是应用考试的办法让学生和教师产生知识的交流，但是由于双方的思维不可直接接触，教师要完全弄清楚学生的思维和想法存在一定难度，所以对于学生的思维，教师在不能表述和理解的同时，也不能故意去抹杀.可以考虑改变以往的封闭式考试模式，提倡和鼓励面对面问答的形式让学生参与考试，避免教师陷入认识封闭境地.

四、总结

尽管有时教师在认识封闭现象中对学生的学习成果有所影响，但是这一问题若能及时被意识到，并正视问题，直面认识封闭现象，这就是数学教学工作者需要具备的科学精神和态度.无论是学生还是教师，都容易陷入认识封闭区域，因此都需要及时认知到这一点，从而认真对待.对此我们可以知道，对于任何一个学科来讲，教学的严谨和科学精神都会经历一系列挑战，这其中包括认识封闭.所以，教师唯有坚持研究“认识封闭”，终将以自己的科学态度战胜认识封闭，迎来教学认识的突破.