一种适用于多普勒高阶变化率的载波跟踪算法

宋青平1，余 跃1，齐建中，王 乐

(1.北京控制与电子技术研究所 信息系统工程重点实验室，北京 100038；2.北方工业大学 电子信息工程学院，北京 100144)

0 引言

在无线通信系统中，当通信发射端和接收端存在速度、加速度、加加速度时，会导致接收端本振与接收信号之间出现多普勒频偏、多普勒一、二阶变化率[1](通常最高只考虑二阶变化率)，从而影响信号的载波跟踪性能。现有的载波跟踪算法通常采用二阶锁频环辅助三阶锁相环[2-4]，可以无误差地跟踪含有多普勒一阶变化率的信号。但是当接收信号由于加加速度而存在多普勒二阶变化率成分时，三阶锁相环会存在一个固有相差，无法保证对此种信号的无误差跟踪。也有文献采用了单一四阶锁相环的方式，但是能够跟踪的频率范围有限，而且缺乏对环路相位误差和环路滤波器参数的系统性分析和计算。

本文提出了一种三阶锁频环辅助四阶锁相环的载波跟踪算法，分析了环路结构，根据环路传递函数和环路带宽，从理论上推导出了环路所有参数的计算方法，以及环路的稳态相位误差。该环路可以对含有多普勒二阶变化率成分的信号进行无误差跟踪。最后采用环路模式切换策略及环路带宽设置策略，进一步提高了频率精度，保证了跟踪的稳定性。仿真结果表明，当存在多普勒频偏、多普勒一、二阶变化率时，本文载波跟踪算法依然能够正常跟踪和解调。

1 频率动态特性

当发射源与接收体之间存在相对运动时，接收体接收的发射源发射信息的频率与发射源发射信息频率不相同，这种现象称为多普勒效应[5-6]，接收频率与发射频率之差称为多普勒频移或频偏。无线电波的传播也存在多普勒效应，当发射源与接收体之间有相对运动时，接收体接收的载波频率f′与发射端载波频率f存在多普勒频移Δf(doppler shift)，即:

Δf=f′-f

(1)

可以证明若接收体与声源相互靠近或相互远离的速度为v，光速为c，则接收体接收信息的多普勒频率为：

(2)

其中:f为发射频率，f′为接收频率。

若物体相对运动时，还存在加速度，加加速度等分量，则相应会产生多普勒变化率等变化量。

接收机接收到信号的频偏可表示为[7]:

(3)

其中:fi表示信号的第i阶变换，例如f0表示多普勒频偏，f1表示多普勒一阶变化率，f2表示多普勒二阶变化率。通常最高只考虑运动的加加速度分量，则可将频偏模型建为:

(4)

对应相位的变化为:

(5)

2 载波跟踪

当数字通信接收机采用相干解调时，接收机首先需要提供一个与发射机载波同频同相的相干载波，这个相干载波的获取就是载波同步，因此载波同步是实现相干解调的前提条件。载波同步首先要生成一个本地振荡信号，本地振荡信号是一个固定频率的自由振荡信号，它往往和输入信号的载波频率不相同，会产生一个频偏；相位噪声也会引起载波相位和频率偏差；同时第1节所述的多普勒效应也会对通信系统产生恶劣影响，使接收系统性能下降。因此，如何抵御噪声的干扰，从噪声中高质量提取相干载波，是载波同步的一个关键技术问题。

载波同步过程通常包括载波捕获和载波跟踪两个阶段[8]。经过载波捕获后，本振与接收信号依然存在一定多普勒频偏、多普勒一、二阶变化率[9]。载波跟踪是在载波捕获完成的基础上，进行载波频率和相位的精细跟踪，实现本地载波与接收信号载波同频同相，从而实现信号的正确解调。载波跟踪原理如图1所示。

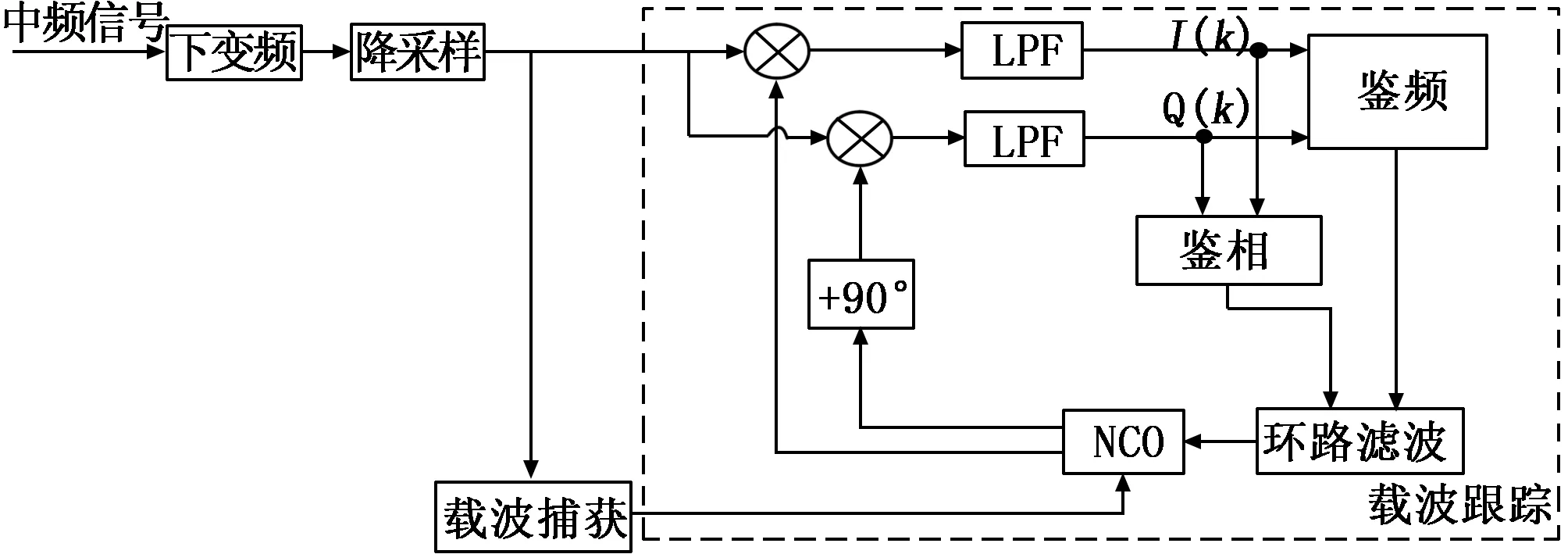
图1 载波跟踪整体结构框图

载波跟踪可分为频率跟踪和相位跟踪，频率跟踪一般通过锁频环实现对载波多普勒频率的本地复现[10]，相位跟踪一般通过锁相环实现对载波多普勒频率的本地复现。多普勒变化率的存在，使得多普勒频差会随着时间急剧变化，从而使得跟踪环路的鉴频和鉴相精度下降，为后级的同步解调带来很大的困难。本文采用三阶锁频环辅助四阶锁相环的跟踪环路，通过环路模式切换及锁频锁相环路带宽设置策略，对较大范围内的频差进行频率牵引，并通过高阶环路的精确鉴频鉴相和滤波，保证了跟踪精度。

3 相位跟踪

相位跟踪通常采用Costas环，结构如图2所示。

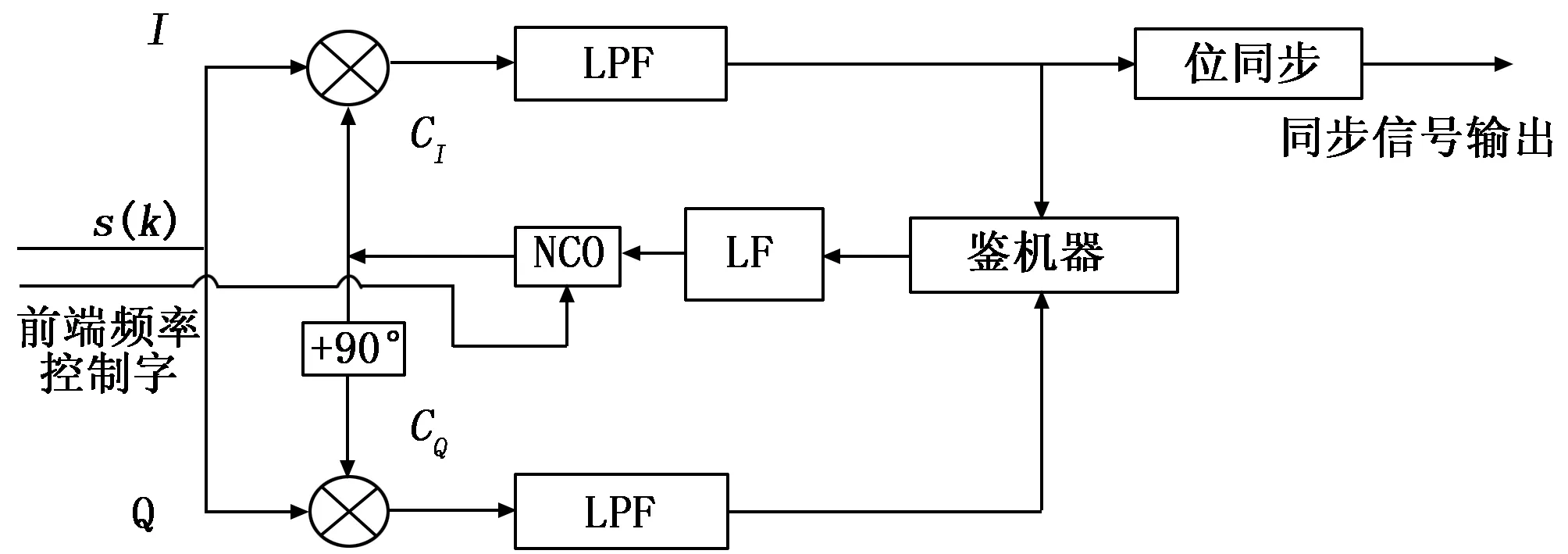
图2 Costas环跟踪单元框图

环路中，本地振荡器(NCO)产生两路相互正交的本地载波信号，与接收信号分别相乘，经过低通滤波(LPF)后滤除倍频项，二者鉴相后可以得到误差信号，经环路滤波器(LF)平滑处理后，输出一个控制信号，反馈至NCO，从而对NCO的频率和相位进行精确调整。

设载波跟踪环路中的输入信号为BPSK调制信号，对输入信号进行数字化采样，设采样频率为fs，采样时间间隔为1/fs，k为采样点序号，则输入信号的时间离散化表示方式如下:

sBPSK(k)=Ab(k)sin(2π(fi/fs)k+ψ)

(6)

式中,b(k)为信息比特，取值1或-1，A为输入信号幅度，fi和ψ分别为输入信号的频率和相位。此时NCO产生的本地载波信号为:

snco_s(k)=sin(2π(f0/fs)k+ψ0)

snco_c(k)=cos(2π(f0/fs)k+ψ0)

(7)

式中,f0和ψ0分别为NCO信号的频率和相位。sBPSK(k)与snco_s(k)和snco_c(k)分别相乘，可得到如下结果:

I(k)=Ab(k)sin(2π(fi/fs)k+ψ)sin(2π(f0/fs)k+ψ0)

Q(k)=Ab(k)sin(2π(fi/fs)k+ψ)cos(2π(f0/fs)k+ψ0)

(8)

经过LPF后输出为:

I(k)=A1b(k)cos(2π(Δf/fs)k+ψ-ψ0)

Q(k)=A1b(k)sin(2π(Δf/fs)k+ψ-ψ0)

(9)

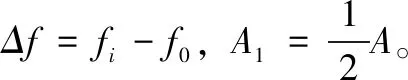
对于相位鉴别器，本文采用反正切鉴相器，鉴相结果表示为[11-13]。

(10)

式中,Δφ=2π(Δf/fs)k+ψ-ψ0。鉴相结果经过LF平滑处理后得到NCO相位控制值。

3.1 四阶锁相环的相位误差

四阶LF的基本传递函数为[14]:

(11)

环路的开环传递函数以及闭环传递函数为:

(12)

(13)

式中，K为环路增益。环路的误差传递函数为:

(14)

当输入信号为多普勒频偏信号时，信号的相位变化为:

θ1(t)=f0t

(15)

环路的相位误差为:

θe=He(s)θ1

(16)

环路稳定后的稳态相位误差为:

(17)

当输入信号为多普勒变化率信号时，信号的相位变化为:

(18)

环路稳定后的稳态相位误差为:

(19)

当输入信号为多普勒二阶变化率信号时，信号的相位变化为:

(20)

环路稳定后的稳态相位误差为:

(21)

由此可以看出，即使当信号由于加加速度而存在多普勒二阶变化率时，四阶锁相环的稳态相差依然为0，可以对此种信号进行无误差跟踪。

3.2 四阶锁相环的环路参数计算

四阶锁相环的LF结构如图3所示。

图3 四阶锁相环LF框图

图中Ts为每次采样时间间隔，pc1～pc4为锁相环LF参数。经过拉式变换后的结构如图4所示。

根据图4，四阶LF的基本传递函数可表示为:

(22)

将式(11)四阶LF的基本传递函数转化为:

(23)

将式(22)和式(23)对比可得:

(24)

(25)

(26)

(27)

其中:τ1、τ2与环路自然角频率、阻尼系数存在如下关系:

(28)

(29)

式中，ωn为环路自然角频率，ξ为阻尼系数。因此，根据ωn、ξ即可计算出τ1、τ2，从而计算出环路参数pc1～pc4。为了保持四阶环路的稳定性，需要满足以下条件[14]。

(30)

(31)

4 载波频率跟踪

锁频环直接跟踪载波频率，通过载波环路鉴频器输出频偏估计误差，具有较好的动态性能。其中叉积锁频环(CPAFC)抗噪声性能较好，且运算量最小，在工程中应用广泛，所以本文选用CPAFC，用来对载波频率进行直接跟踪。叉积鉴频器由同相和正交信号的叉积运算获得，可以去除相位信息。鉴频后的误差信号经过LF平滑处理后，反馈至NCO，控制NCO的振荡频率向接收信号频率靠近，最终使频差接近为0。锁频环的输出为频率分量，接入LF后经过积分，使得频率转化为相位。锁频环的环路阶数通常比锁相环低一阶，当锁相环为四阶时，锁频环为三阶。CPAFC环路结构如图5所示。

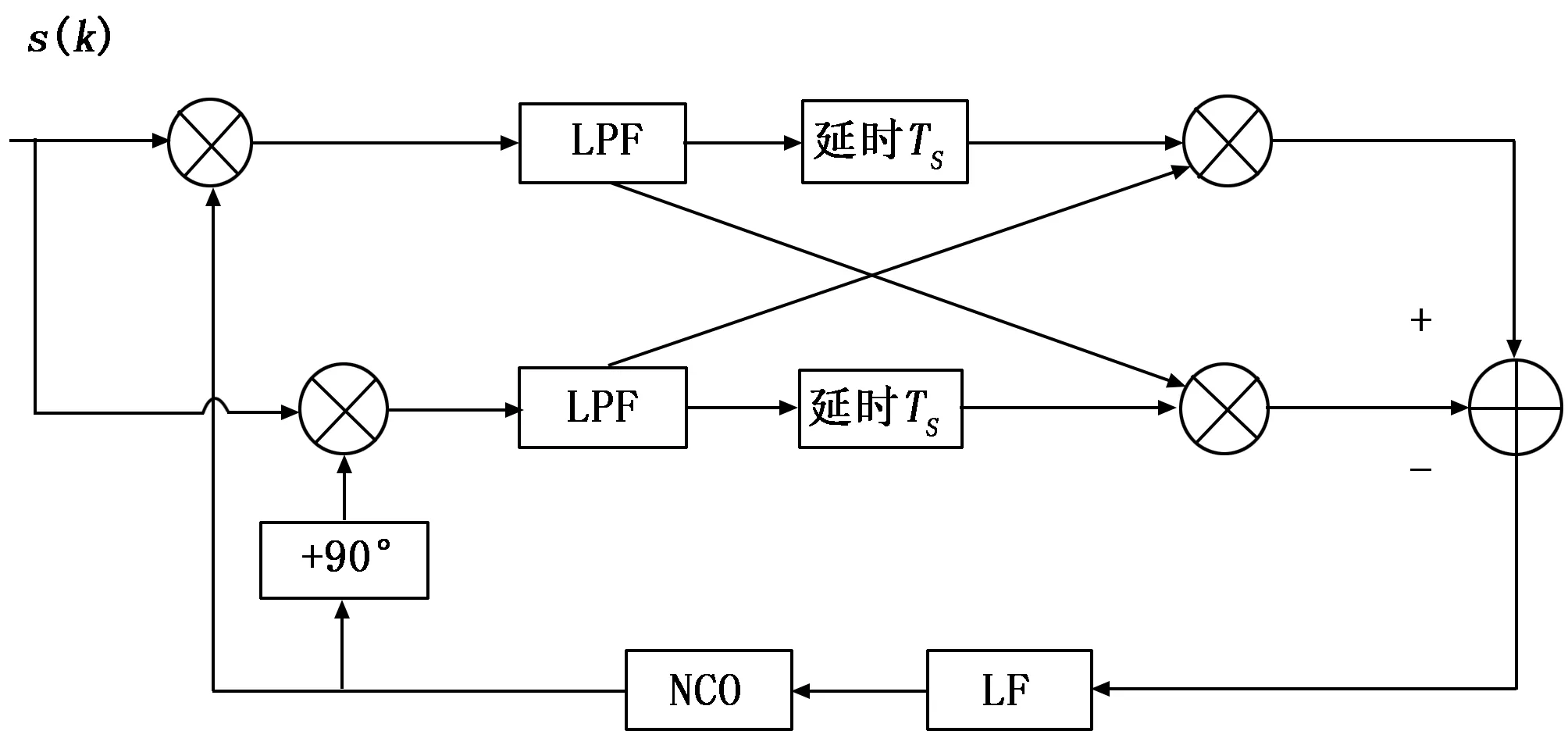
图5 CPAFC频率跟踪单元框图

对于式(9)中经过LPF的I(k)和Q(k)，叉积运算后的输出表示如下:

Ecross(k)=I(k-1)Q(k)-I(k)Q(k-1)

(32)

则由式(32)可得:

Ecross(k)=A2sin(2π(Δfd/fs)k)

(33)

式中,Δfd为多普勒频率估计残差。鉴频器输出的频率误差为:

(34)

对于三阶锁频环，LF结构如图6所示。

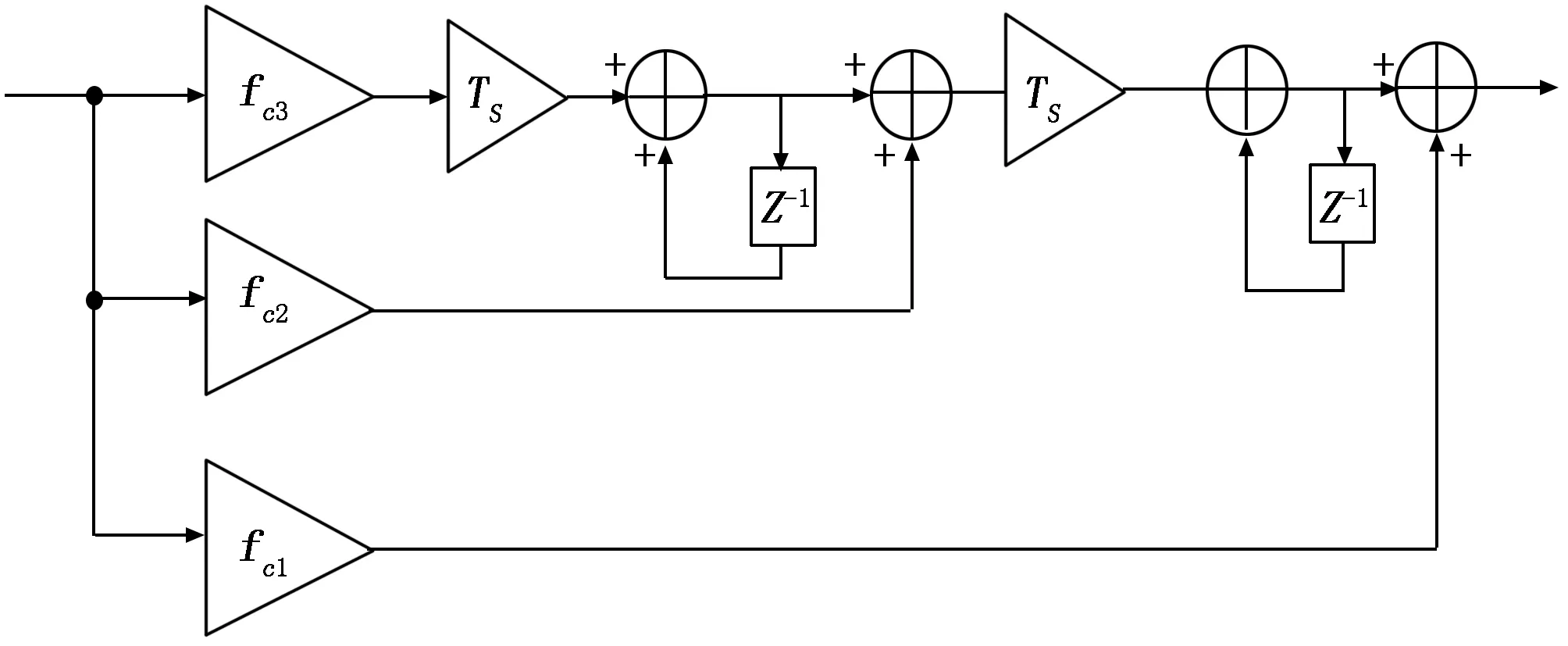
图6 三阶锁频环LF框图

图中，fc1～fc3为锁频环的LF参数。LF采用通用的三阶环路参数计算方法，表示如下：

ω0f=Bnf/0.7845

(35)

fc1=2.4ω0f

(36)

(37)

(38)

其中:Bnf为锁频环环路噪声带宽，Ts为每次采样时间间隔。

5 三阶锁频环辅助四阶锁相环

锁频环用于跟踪较大的多普勒初始频差和变化率，通过精确的频率鉴别，将计算得到的多普勒频率信息传递给锁相环。四阶锁相环能无误差跟踪含有多普勒二阶频率变化率的信号，但是在锁相环路开始工作时，仍然需要较为准确的多普勒频差及变化率信息才能快速入锁，而且锁频环的跟踪门限比锁相环低，具有良好的动态及抗干扰性能，但锁频环的缺点是频率跟踪误差较大。锁相环能够精确跟踪信号相位，跟踪误差较小，但是动态范围也较小。所以采用三阶锁频环辅助四阶锁相环的工作方式，可以既提高整个环路的闭合速度，降低信噪比门限，又能保证跟踪精度。

图7给出了三阶锁频环辅助四阶锁相环的LF结构框图。该环路对来自锁频环和锁相环的鉴别误差同时加以应用，因此对相位抖动较为敏感的同时具有较宽的动态范围。图7中fc1、fc2、fc3可由式(36)～(38)得出，pc1、pc2、pc3、pc4可由式(24)～(27)得出。锁频环的作用是为了提高锁相环的跟踪范围，但锁频环永久接入并非能持续保证良好的性能，信噪比较低时，鉴频器难以区分信号和噪声，并且在图7中的LF工作过程中，是将锁频环输出的频率误差和锁相环输出的相位误差进行融合处理，这种处理方式会引入较大的环路误差，因此锁频环和锁相环同时工作的方式会使得环路误差增大。所以锁频环完成频率牵引后，可以关闭锁频环，转为单一的锁相环工作模式，进一步提高频率精度。

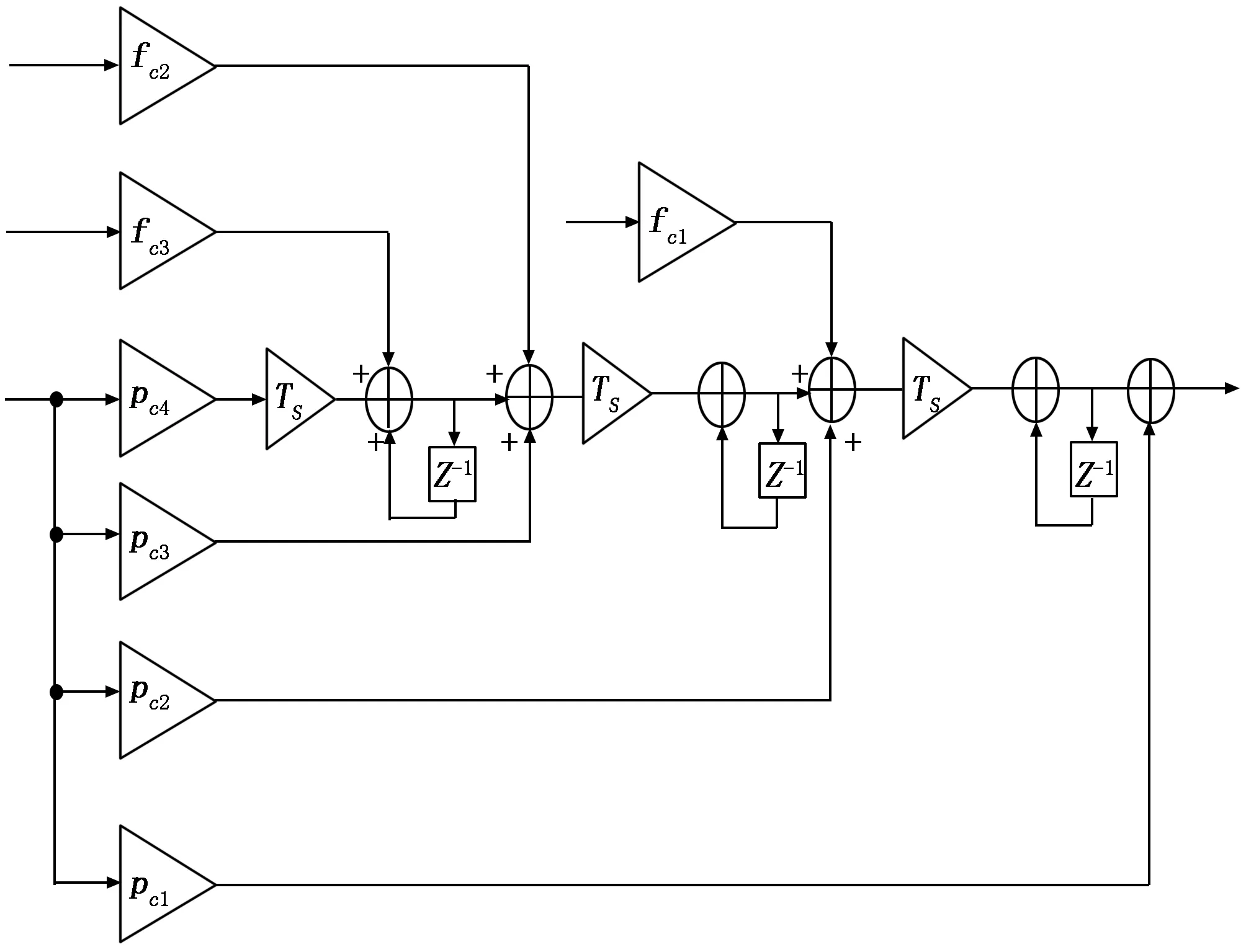
图7 三阶锁频环辅助的四阶锁相环LF设计框图

锁频锁相环路能捕获跟踪的多普勒频偏和变化率大小和接收信号的信噪比是一对矛盾约束关系。当需要跟踪的频偏和变化率较大时，则噪声带宽需要设置的较宽，但较宽的环路带宽会导致进入环路的噪声功率增加，使得环路的信噪比恶化。为了能正确解调出原始信号，环路内的信噪比必须保持在某个门限值以上，所以信号本身的信噪比就不能太低。反之，当信号本身的信噪比较低时，要想成功捕获跟踪载波信号，则环路噪声带宽需要设置的较窄，这样，进入环路的噪声功率会相对较小，依然可以保持环路内的信噪比在门限值以上，但是此时对频偏和变化率的跟踪能力就相对较差，而且当频率变化较快时，则环路有可能永远无法达到稳态，即LF的输出变化永远跟不上输入信号频率的变化。因此，本文在锁频环和锁相环初始同时工作时设置较大的锁频环带宽值，关闭锁频环之后，设置较小的锁相环带宽值或环路自然角频率。这种设置方式可以保证在频率牵引阶段，环路能够跟踪的频偏和变化率范围较大，锁定时间也较短；在单一锁相环工作阶段，环路能够保持稳定跟踪并开始解调信号。

6 算法仿真

针对本文提出的算法进行仿真。采样频率取为4 kHz，码速率取为100 bps，多普勒频偏取为300 Hz，多普勒变化率取为50 Hz/s，多普勒二阶变化率取为10 Hz/s2，加入高斯白噪声，比特信噪比Eb/N0取为12 dB。锁相环环路自然角频率设为4π，为了增大频率牵引范围，锁频环环路噪声带宽设为30 Hz。当环路增益K取为1，阻尼系数ξ为0.707时，经过计算得到的τ1、τ2满足式(30)、(31)的环路稳定性条件。仿真过程中取前20 000个采样点，在10 000个采样点处关闭锁频环。

频率鉴别结果如图8所示，接收本振频率跟踪结果如图9所示。从图8可以看出，鉴频误差小于0.1 Hz；从图9可以看出，锁频环辅助锁相环状态可以快速消除多普勒频偏、多普勒一、二阶变化率，快速达到锁定状态，但此时本振频率误差较大，当转变至单一锁相环精确跟踪状态后，可以看出本振频率误差明显减小，并且频率抖动幅度恒定。

图8 频率鉴别后结果

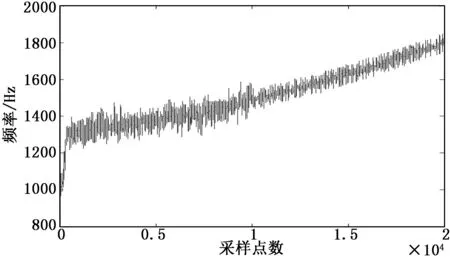
图9 接收本振频率跟踪图

图10为LPF输出的解调后的原始信号波形。可以看出，经过本文环路跟踪解调后，可以正常恢复出原始数字方波信号。

7 结论

本文针对多普勒条件下的载波跟踪问题，提出了一种三阶锁频环辅助四阶锁相环算法，首先从理论上证明了该环路能够无误差跟踪多普勒二阶变化率信号，然后根据环路传递函数和环路带宽，推导出了环路所有参数的计算方法，并在环路设计中考虑了环路的稳定性条件，最后通过环路模式切换，既提高了整个环路的闭合速度，降低了信噪比门限，又保证了跟踪精度。因此，此法在多普勒高阶变化率的情况下具有较高的应用价值。