移动机器人导航系统中的车道线检测方法及实现

2222

(1.芜湖安普机器人产业技术研究院有限公司 研发部，安徽 芜湖 241007;2.芜湖安普机器人产业技术研究院有限公司 院士工作站，安徽 芜湖 241007;3.安徽工程大学 机械与汽车工程学院，安徽 芜湖 241000)

0 引言

GPS与惯性导航技术一直是室外移动机器人的重要导航方式之一。但是，在不使用RTK技术时，民用GPS的定位精度通常最高只能做到动态误差1米左右，静态误差1.5米左右，在很多工况下，这种精度并不够；同时，当周围建筑物较多的室外环境下，GPS信号容易受遮挡并丢失信号，造成GPS定位不准或者根本不能定位；当失去GPS信号后，如果以纯惯性导航模式工作时，其误差将随着导航时间增加而累积[1]，所以很难依赖纯惯导模式单独工作。为弥补GPS与惯性导航组合不足之处。提出采用机器视觉识别车道线作为辅助定位技术手段。当前，车道线检测广泛应用于汽车的无人驾驶过程，常用于车道偏离报警、高级辅助驾驶等。通过识别路面车道线，对是移动机器人GPS+惯性导航进行补充修正，提高移动机器人室外导航的可靠性及稳定性。

路面车道线检测基本流程可以分解为以下几个步骤[2]：系统读取图像信息，对读取到的图像信息做灰度处理，对图像做二值化处理，提取图像的边缘特征并进行滤波处理，霍夫变换，最后计算移动机器人相对车道线的偏转角度和偏离距离。

1 车道线检测预处理

1.1 图像的灰度处理和降噪处理

因为摄像头采集的是彩色图像，而彩色图像信息量非常大，为了不影响系统处理的实时性，需要先对图像做灰度处理。灰度处理后信息量较少但是能非常好的读取R、G、B三方位的信息量[3]。因为移动机器人测试的路面主要集中在柏油路面，道路的背景色偏黑色，同时获取的路面车道线信息主要是白色和黄色两种，所以在对路面图像灰度化处理中给予G方位信息较大权重，从而将车道线信息从路面背景图像中突显出来。

灰度处理可表示为：

f(i,j)=a×R(i,j)+b×G(i,j)+c×B(i,j)

(1)

其中：f(i,j)为处理后的灰度图，R(i,j)、G(i,j)、B(i,j)分别表示R、G、B三方位的信息量。根据以往经验，a=0.3，b=0.59，c=0.11。

车道路面图像信息主要是加性干扰噪声，由于受到天气、周围环境以及传感器自身的电子噪声干扰影响，图像信息在传输过程中，会受噪声信号影响而失真。为了降低噪声对后续处理过程的影响，需要消除噪声信号。

为了提高图像处理的实时性，采用空域滤波器进行降噪处理。常见的空域滤波器分为线性滤波器和非线性滤波器。线性滤波器在使用过程中，会使得图像中的车道线边缘和轮毂信息变得模糊，在后续处理过程中，降低车道线信息的识别率，为了既能有效降低图像噪声提高图像质量，又不会使车道线信息过分丢失，采用非线性滤波器对图像进行降噪处理。

中值滤波器是一种常见的非线性滤波器，具有算法简单，实时性好的优点。其基本原理是将读取到的图像中某一像素邻域的像素值按照大小进行降序排列，并将获取到的中间值作为这个像素点的灰度值。

中值滤波器的表达式可表示为：

f(i,j)=median{Sf(i,j)}

(2)

上述公式(2)中：{Sf(i,j)}是像素点f(i,j)的领域。

1.2 图像感兴趣区域划分

在进行车道线检测的过程中，通常图像的上半部分是天空或者其它背景部分，而路面车道线等关键信息则主要出现在图像的下下半部分。为了提高系统工作的准确性以及实时性，滤出图像中其它无关信息的干扰，需要系统只对感兴趣的区域进行搜索，这样就需要对图像的感兴趣区域进行划分。

假设从视觉摄像头上获得的原始路面图像信息是Im×n，m和n分别表示图像Im×n的行数以及列数。在视觉摄像头固定到移动机器人车体上后，路面车道线图像感兴趣区域的下部分边界就处于车体前部的某一个固定区域，车道线图像感兴趣区域的上半部分位于两条车道的交汇处，这个交汇区域也基本是固定的。因此，路面车道线图像感兴趣区域就位于下半部分边界区域以及上半部分边界车道线交汇区域内。

k1和k2与原始图像Im×n的关系可以表示为：

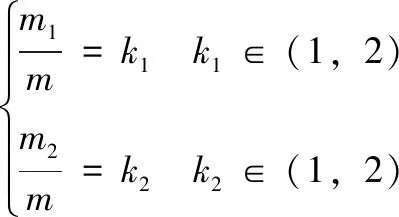
(3)

上述公式(3)中m1和m2分别是上边界和下边界在原始图像中像素点的行数，k1和k2分别是上边界与下边界与原始图像之间比值，且根据实际测量结果，令k1=0.6，k2=0.2。

1.3 图像的二值化处理

在对采集到的车道线视频图像做灰度处理后，为了使车道线轮廓更突显，剔除更多干扰信息，提高系统的鲁棒性及实时性，还需要对图像作二值化处理。文章采用Otsu算法对图像做二值化处理[4]。

Otsu算法又称为最大类间方差法或大律法，其基本思路是按照图像灰度特性(某个阀值T)分割 的图像像素点两部分(车道线像素和背景像素集)的最大类间方差σ2。类间方差σ2越大，车道线像素集和背景像素的差异就越大，二值化效果就越好[5]。Otsu算法的二值化阀值确定如下：

σ2(t)=ω1(t)(μ1(t)-μ)2+ω2(μ2(t)-μ)2

(4)

其中：t为某个时刻阀值，t1为被背景像素集，ω1灰度平均值，μ2为车道线像素集,ω2灰度平均值，μ为整幅图像的平均灰度值。t∈{0,1,2,3,…,L,…,255}，arg表示求反函数。

二值化处理过程如下式(3)：

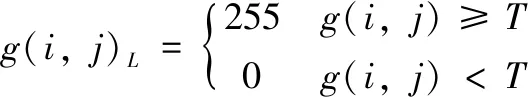
(5)

其中：g(i,j)L为二值化处理后图像，g(i,j)为处理前的灰度图。

1.4 改进型小波阀值函数与Canny算子融合

图像边沿特征提取是对图像剧烈变化或者不连续的像素点的集合，如灰度值突变、颜色突变、结构突变的像素点等。图像的边沿特征提取是车道线检测的一个重要环节，边缘特征信息提取的准确性对系统的检测效果有着重要影响。常用的边缘检测算子有Canny检测算子、LOG检测算子、Soble检测算子。由于Canny检测算子具有检测精度高、检测速度快的特点，因而应用较为广泛。

传统的Canny检测算子边缘特征提取可分为以下几个步骤[6]：

1)采用高斯滤波器对图像进行平滑处理；

2)计算梯度的幅值方向；

3)非极大值抑制；

4)采用双阀值算法对边缘作检测和连接。

上述第一步的高斯滤波器，传统方法是采用二维高斯函数下式(7)来构造滤波函数，过程是先对原始图像按行和列作平滑处理，σ是高斯函数的标准差，决定了函数的平滑程度；然后采用下式(7)计算I在(i,j)处垂直和水平方向上的偏导数；之后根据下式(8)分别计算出I在(i,j)处的梯度模和梯度方向；若图像I在(i,j)处的像素点梯度模大于或等于沿梯度方向两个相近像素点的梯度模，则说明这个当前的像素点可能是边缘点；最后使用双阀值算法对边缘作检测及连接。

(6)

(7)

上述公式(7)中:Gx[x,y]为水平方向偏导数，Gy[x,y]为垂直方向偏导数。

(8)

上述公式(8)中：M(i,j)为梯度模,θ(i,j)为梯度方向。

传统的Canny算子边沿特征提取算法因为首先使用高斯低通滤波器对图像作平滑处理，但是高斯滤波器存在对图像的过度平滑问题[7]，为了改善边沿特征提取效果，提出一种改进型的小波阀值算法代替高斯滤波器对图像进行平滑处理，取得了较好的效果。

常见的小波阀值函数分为软阀值函数和硬阀值函数两种[8]，文章采用一种新的小波阀值函数如下：

(9)

当参数m=1时，改进型阀值函数与软阀值函数的曲线几乎重合；当m>1时，函数的曲线逐渐接近于硬阀值函数。

使用改进型小波函数与Canny算子边缘检测的相融合的算法处理过程如下：

1)对原始含噪图像f(i,j)使用Canny算子作边缘检测，并得到处理后的边缘图像fe(i,j)；

2)对原始图像f(i,j)和处理后的图像fe(i,j)作3层小波分解，分别得到小波域图像Wf(i,j)和Wfe(i,j)；

4)对图像的对应像素使用公式(10)作加权处理,其中加权系数r∈(0,1)；

(10)

第五步：对双阀值处理得到的图像W作小波变换，得到最终的重构图像。

下图分别是传统Canny算子边缘提取算法和改进型算法的效果对比：可以看出相对于传统Canny算法，改进型算法通过选择合适的小波阈值参数m值，图像边缘的细节特征保留更好，车道线的轮廓清晰；传统的Canny算法由于高斯滤波器对图像的过渡平滑而造成车道线的边缘模糊且有不同程度的信息丢失[9]。

图1 原图像的边沿特征提取 图2 传统Canny算子边沿特征提取

图3 改进型Canny算子边沿特征提取

为了定性分析实验结果，使用方差、平均梯度、信息熵作为评价指标。方差评价灰度值的分散程度；平均梯度评价图像清晰程度，也就是图像边缘细节的保留程度，这是分析的关键指标；信息熵评价图像灰度值的一致性。

根据表1可知，从平均梯度值来看，使用改进的小波阀值函数与canny算子融合，相对于传统的高斯滤波器与canny算子融合，前者的平均梯度值较大，说明改进型算法在保留边缘细节信息上效果较为明显，也就是边沿特征提取的效果更好。从信息熵来看，改进的小波阀值函数与canny算子融合算法的值比传统算法值大，则说明改进型算法保持灰度的一致性效果更好。综上，改进的小波阀值函数与canny算子融合算法相对于传统高斯滤波器与canny算子融合算法有优势。

1.5 霍夫变换

最后采用霍夫变换，识别图像中感兴趣区域的中的直线。霍夫变换是一种用于机器视觉、图像分析处理、数字图像处理等的一种图像特征提取技术。常用于检测图像中的直线特征集合点。在一个直角坐标系中，过其中点A(x1,y1)的直线可以描述为：y1=kx1+b，过其中另一点B(x1,y2)的直线描述为：y2=kx2+b。如果把上述两组方程视作(k,b)参数空间表达式，那么上述两个方程的解即通过点A(x1,y1)和点B(x1,y2)的直线。

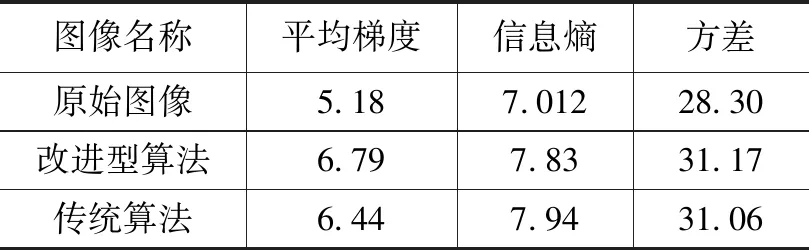
表1 两种算法参数评价

之后把原直角坐标系的点转换到极坐标系，则两点A(x1,y1)和B(x1,y2)在参数空间(ρ,θ)表示为两条曲线。A和B在极坐标系内的交点就是二者在直角坐标系中经过A.B的直线，这时ρ就是直线到原点之间的距离，θ就是直线与x轴之间的夹角[10]。即说明当直角坐标系中的任意一点转换到极坐标下时，则表达为一条正弦或余弦曲线，而当任意两条曲线在极坐标系(ρi,θi)处有交点，则说明这条曲线在直角坐标系中相应的处于斜率-截距的参数空间(ki,θi)上。

具体转换关系如图4所示。

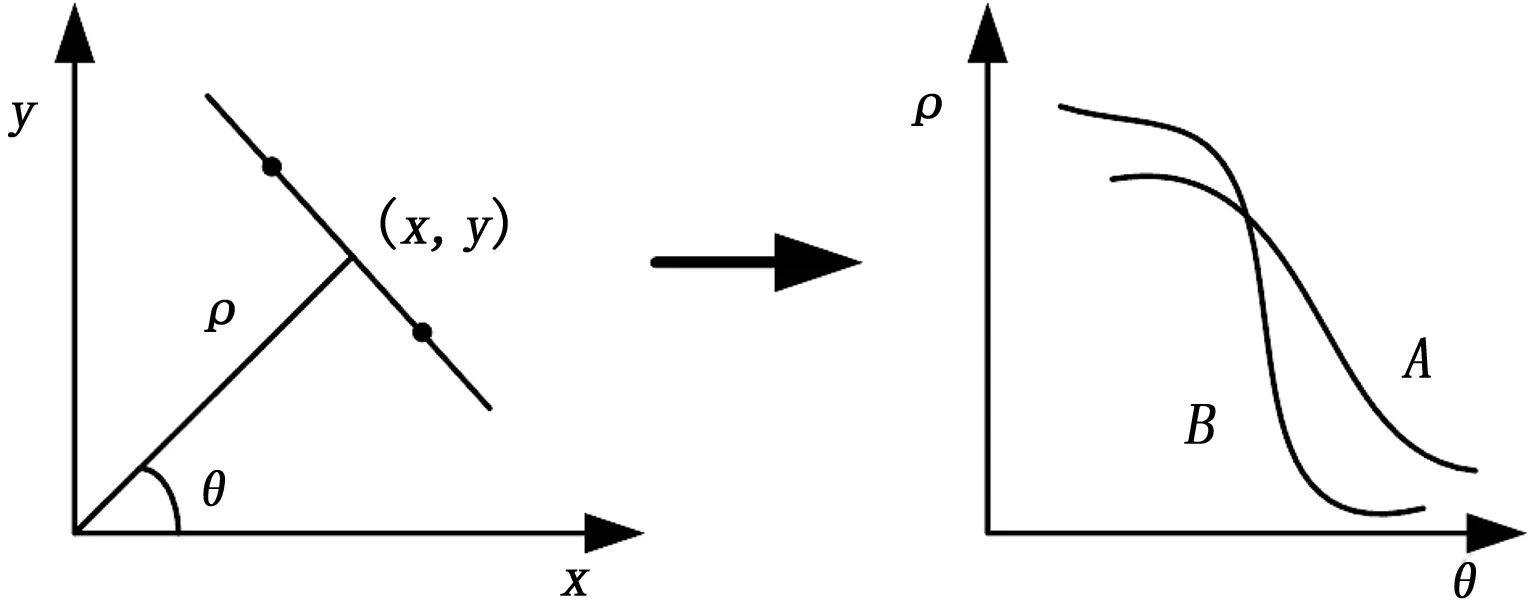
图4 霍夫变换原理图

由霍夫变换的原理可得知，在极坐标空间中曲线可由任意两点构成，曲线的交点在参数(ki,bi)确定的直线上。由此，我们可以确定在原图中是否存在该直线。

在使用霍夫变换时，通常采用投票方式对图像中的直线进行统计。预先设定阈值η，当处于(ki,bi)上的点的数量大于阈值η，则可以认定确实有一条直线y=kix+bi存在于图像中。在直角坐标系中的参数(k,b)和极坐标系中的参数(ρ,θ)是相互对应的，其关系如下所示：

(11)

上述公式(11)中：ρ为直线与原点间的距离，θ为直角坐标系下直线与横坐标之间的夹角。

通过霍夫变换之后，直角坐标系(x,y)平面内的直线就被映射到了极坐标系平面。统计处于极坐标系参数(ρi,θi)上点的数量，当其中的点数量达到预先设定的阈值η时，则可以确定其中的一条直线[12]。

在实际测试过程中，为了方便编程，采用如下方法获取交点：设某图像的对角线为n，ρ∈[0,n]，θ∈[-π/2,π/2]，使用二维数组Hough[ρ][θ]用来统计处于(ρ,θ)参数空间中的交点数，其中θ将1°作为基本增量单位，ρ将1作为基本增量单位，增量单位愈小则计算愈精确。

2 移动机器人偏离车道线的角度及距离测算

2.1 系统模型及参数

将视觉摄像头安装于机器人前方，记录摄像头的安装高度h和俯角θ，参数h和θ在机器人移动期间为固定参数。因此，机器人的位置可以由偏转角度β和到车道线的偏离距离d决定[13]。系统模型如图5所示。

图5 系统模型

将摄像头作为坐标原点O，并建立空间坐标系，将摄像头朝向定义为Z轴，和路面相交于D点，OQ为摄像头的高度h，∠ODQ为摄像俯角θ。

在ODQ平面内，离z相较于图像尺寸u、v很大时，其变换关系可由下式(12)过O点作OD垂线与路面相交于E点，OE定义为y轴，过O点作ZOY平面的垂线，定义为x轴。从而xyz构成了一组空间直角坐标系。同时，在图像平面建立一组二维坐标系，图中的点O′作为原点，其横坐标分别为u、v。当成像距)表示：

(12)

其中：f定义为成像系统焦距。

在移动机器人与车道线停放夹角为β=45°情况下，通过下式(13)推导出来：

(13)

其中：θ为摄像头俯角，n0和m0分别是每一帧车道线的直线方程参数。

2.2 移动机器人偏离车道线参数计算

根据摄像头的高度h、俯角θ和测算得到的f，可以计算出移动机器人的偏转角β和相对车道线的偏离距离d。取车道线上的任意一点P，其在空间坐标系xyz中的坐标为(a,b,c)，P′为其在拍摄图像中的对应的像素点，可以推导出以下两个表达式：

ncosθcosβ+fsinθcosβ-mfsinβ=0

(14)

mhsinθsinβ+mdcosθ-hcosβ=0

(15)

根据上式(14)和(15)可以计算出偏转角β和偏离距离d。

(16)

(17)

其中：f定义为成像系统焦距，h为摄像头高度值，θ为摄像头的俯角[12]。

3 实验结果

为了模拟移动机器人在普通路面上移动的情况，采用在公路上的5段行车记录仪视频作为模拟，对每段行车视频采样2400帧图片，并对最终采集到的车道线视频图像通过matlab仿真软件进行计算。下图6和图7是任意两张从系统中截取的实时图像信息，蓝线部分及为系统识别到的车道线信息。

图6 第1帧图片

图7 第1280帧图片

表2是图6和图7对应的偏转角度β和偏离距离d。采用3.2节的偏离车道线参数计算方法，实时获取到了当前偏转角度β和偏离距离d。系统实时识别了当前第1帧图像中的偏转角度β=4.922379°，偏离距离d=1.13754 m，第1280帧图像中偏转角度β=7.138246°，偏离距离d=0.870839 m。实验达到了预期效果。

4 结论

文章在GPS与惯性导航基础上增加了视觉检测车道线作辅助定位手段。提出了一种改进型边沿特征提取算法，使用改进型小波阀值算法代替传统的高斯滤波器，对图像进行平滑及降噪处理，并取得了较好的效果。最后对视频进行车道线检测，采样了12 000帧图像，分别实时获得了每帧车道线图像的偏转角度β和偏离距离d。实验发现12 000帧图像中有仅有892帧图像检测失败，成功率达到92.6%，取得了较好的效果。模拟仿真实验对下一步进行移动机器人自主导航测试打下了良好基础。

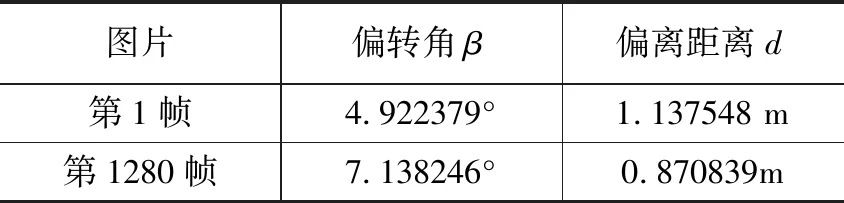
表2 偏转角度和偏离距离值实验数据表