一种枪械射弹散布预测方法
2019-09-25张晓云杨宇召
张晓云,杨宇召,徐 诚
(南京理工大学 机械工程学院,江苏 南京 210094)
枪械的射弹散布是射击精度的重要指标之一,而提高射击精度一直是世界各国的研究重点。美国的Celmins[1]对5.56 mm M855弹的散布进行了测试,重点研究了该型号弹由M4发射时的跳动特性。在试验数据的基础上,针对系统的误差源进行了量化分析。国内相关研究人员也对枪械射弹散布进行了一定的研究,研究重点主要集中在试验与验证匹配上。
在枪械的实际射击过程中,影响射弹散布的因素很多,其中还包括内弹道、外弹道过程中产生的各种随机因素。为了在设计研发或者论证阶段对枪械的射弹散布进行快速研究分析,近年来,越来越多的仿真技术被应用到枪械各个弹道阶段的研究中,为射弹散布的预测提供了理论基础和实现手段。
在枪械内弹道研究方面,王瑞[2]采用MATLAB软件建立了某5.8 mm自动步枪的随机内弹道模型,结合在ADAMS软件中建立的自动机动力学模型,进行了弹药和自动机相关参数的随机数值模拟实验。通过数值模拟,得到了弹丸初速分布的变化规律,并分析了各生产制造误差对弹丸初速稳定性的影响。在弹/枪相互作用研究方面,刘国庆等[3-5]基于非线性有限元理论,建立了弹/枪膛内相互作用数值计算模型,在此基础上提出了某高精度狙击步枪的弹/枪匹配设计方法,在设计阶段优化了弹/枪参数。他们在匹配优化设计中,引入弹丸质量偏心为误差源,并考虑了其对弹丸摆动角的影响。杨宇召等[6]则通过枪管和弹丸壳体材料力学性能试验,明确了某型枪弹材料的相关材料参数,建立了铜被甲弹丸的网格模型和材料模型。通过ABAQUS软件的数值模拟,研究了铜被甲弹丸从挤进到出膛的运动姿态,分析了温度对弹丸在膛内摆动的影响。国外的Liennard等[7],为了提高某枪械的射击精度,研究了枪管直线度对弹丸出膛状态的影响。他们同样建立了相应的弹/枪相互作用有限元模型,并通过测量枪管的周向应变与LS-Dyna的仿真结果对比,验证了模型的准确性。在此基础上,采用仿真的方法,定量分析了4种不同直线度的枪管模型对弹丸出膛偏角和速度的影响。
在枪械外弹道研究方面,常用的外弹道计算模型有质点外弹道和六自由度模型。对于口径较小的枪弹,常使用质点外弹道估算其外弹道性能。除了用高级语言编程进行外弹道建模计算,还可采用MATLAB/Simulink搭建系统模型,很大程度上缩短了建模的时间[8]。柏迅等[9]深入研究了弹着点相对于预估点的随机性,基于蒙特卡罗法,通过MATLAB产生随机数,用C++语言进行了外弹道方程的解算,建立了随机外弹道模型。在此基础上分析了初速、射击、横风等各随机因素影响下的枪弹弹丸外弹道散布特性。
迄今为止,通过全弹道预测枪械射击精度的方法很少报道。本文在现有研究的基础上,以某型5.8 mm自动步枪及5.8 mm通用弹为例,提出一种枪械协同仿真模型预测方法,可以在设计阶段方便快捷地对枪械精度进行有效的预测与评估,缩短研发周期。
1 基本原理与方法
1.1 协同仿真模型
本文提出的枪械协同仿真模型主要由枪械随机内弹道模型、弹/枪相互作用模型和质点外弹道模型组成,通过全弹道模型来预测枪械的射击精度。协同仿真各模型之间的联系和相关参数传递过程如图1所示。图中,p-t表示膛压p随时间的变化,Δpm为最大膛压的变化值;θ0为弹丸初始射角;Δθ为弹丸质心速度偏角;v0为弹丸初速;Δv0为初速的偏差;R50,R100分别为包含50%和100%弹着点的最小圆半径。首先,在经典内弹道方程的基础上,引入随机变量进行抽样,构建随机内弹道模型,然后将计算所得的膛压变化结果传递给弹/枪相互作用模型。弹/枪相互作用模型建立在有限元模型的基础上,可以通过数值模拟的方法,得到弹丸在膛内运动的情况。将弹/枪相互作用模型计算得到的弹丸初始偏角传递给外弹道模型,同时结合随机内弹道模型得到的弹丸初速及其偏差,通过外弹道模型的多次计算得到射弹散布。

图1 协同仿真模型参数传递过程
1.2 随机内弹道模型
在经典内弹道模型的基础上建立枪械随机内弹道模型。经典内弹道方程组包括:火药燃气生成函数、燃烧速度方程、能量转换方程、弹丸运动方程和弹丸运动与行程关系式,各方程如下[10]:
(1)
(2)
式中:ψ为火药燃烧的相对质量;χ,λ,μ为火药形状特征量;Z为火药相对已燃厚度;u1为火药燃烧系数;δ1为1/2火药药厚;p为膛内平均压力;n为燃速指数;φ为次要功系数;mp为弹丸质量;v为弹丸速度;S为线膛内横断面积;Lψ为药室自由容积缩径长,即以火药燃烧ψ时药室中的自由容积Vψ除以S所得的长度;l为弹丸行程;f为火药力;mc为装药量;θq为绝热系数;V0为药室容积;ρm为火药密度;α为火药气体余容。

1.3 弹/枪相互作用模型
弹丸在膛内不仅具有轴向运动与旋转运动,而且还会出现绕弹轴的摆动,这将对枪管本身产生较大的振动激励,从而影响弹丸在膛内及出膛时刻的运动状态。此外,枪管结构参数的改变与弯曲等状态也会影响弹丸的膛内运动,弹丸运动与枪管振动相互耦合决定了弹丸出膛的最终状态。
本文根据某型号5.8 mm自动步枪及其弹丸的结构参数,建立了三维实体模型,采用Hypermesh软件对其进行了网格划分,网格类型以六面体网格(C3D8R)为主。考虑到弹丸的变形(尤其是铜被甲的变形)较大,所以弹丸的网格密度要高于枪管内表面的网格密度,各部分具体网格数如表1所示,枪管和弹丸相互作用的有限元模型如图2所示。

表1 各部件网格数
考虑在重力影响下枪管会出现弯曲,对弹丸运动有一定的影响,所以对枪管模型施加重力载荷,并约束枪管尾部全部自由度。膛内火药气体燃烧产生的压力载荷施加在弹丸底部及尾锥部表面,如图3所示。

图3 火药压力载荷的施加
枪管、铅套和钢芯的相关材料力学性能(弹性模量E、泊松比μ和密度ρ)如表2所示。

表2 枪管、铅套和钢芯材料力学性能
铜被甲材料的力学性能采用Johnson-Cook本构模型来描述[13]:
(3)

铜被甲Johnson-Cook材料参数的定义参考文献[13],具体如表3所示。

表3 铜被甲材料参数
1.4 外弹道模型
在枪弹外弹道计算中,经典质点外弹道模型较为常用,其计算主要参数包括弹丸初速、弹丸质量、射角以及弹形系数(或弹道系数)等,该模型可以计算弹丸在弹道上各点的速度、位移等参数。对于步枪弹而言,质点外弹道模型虽然较为简单,但对于估算弹丸的落点状况具有一定的意义。
质点外弹道的基本方程为[14]
(4)
式中:H(y)为空气密度函数,有
(5)
G(v)为空气阻力函数:
G(v)=4.736×10-4vCx,on(v/cs)
(6)
式中:c为弹道系数;v为弹丸初速;vx为弹丸速度水平分量;vy为弹丸速度垂直分量;θ0为初始射角;ρ,ρon分别为地面空气密度和标准空气密度;p,pon分别为地面实际气压和标准气压;τ,τon分别为地面气温和标准气温;cs为声速;Cx,on(v/cs)为标准弹阻力系数。积分起始条件:t=0,vx=v0cosθ0,vy=v0sinθ0,其中,v0为弹丸初速。
本文所提协同仿真模型中的外弹道模型的初始参数(初速及射角偏差)由内弹道模型和弹/枪相互作用模型计算结果得到。
2 仿真实例与试验对比
2.1 随机内弹道计算结果
采用本课题组自编的弹道计算程序进行随机内弹道计算,随机参数包括弹丸质量和装药量等,其界面如图4所示。对弹丸质量和装药量在正态分布范围内进行20组随机抽样,结合经典内弹道方程进行随机内弹道计算,得到的膛压曲线如图5所示。

图4 随机内弹道计算程序
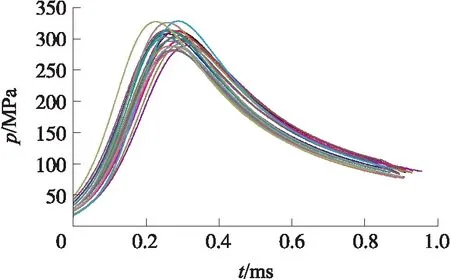
图5 20组随机内弹道膛压曲线
各算例的弹丸质量和装药量的抽样如表4所示,弹丸初速的随机散布结果也在表4中列出。

表4 内弹道计算结果
2.2 弹/枪相互作用计算结果
在随机内弹道结果的基础上,将相应的膛压载荷施加到弹/枪相互作用有限元模型上,采用ABAQUS软件,分别对20组数据进行仿真,得到了内弹道随机偏差对弹丸出膛时刻状态的影响。弹丸出膛时刻的质心速度偏角如表5所示,表中,横向偏角θx较小,在-0.01°~0.1°范围内变化;纵向偏角θy角度较大,在-0.21°~-0.03°范围内变化。
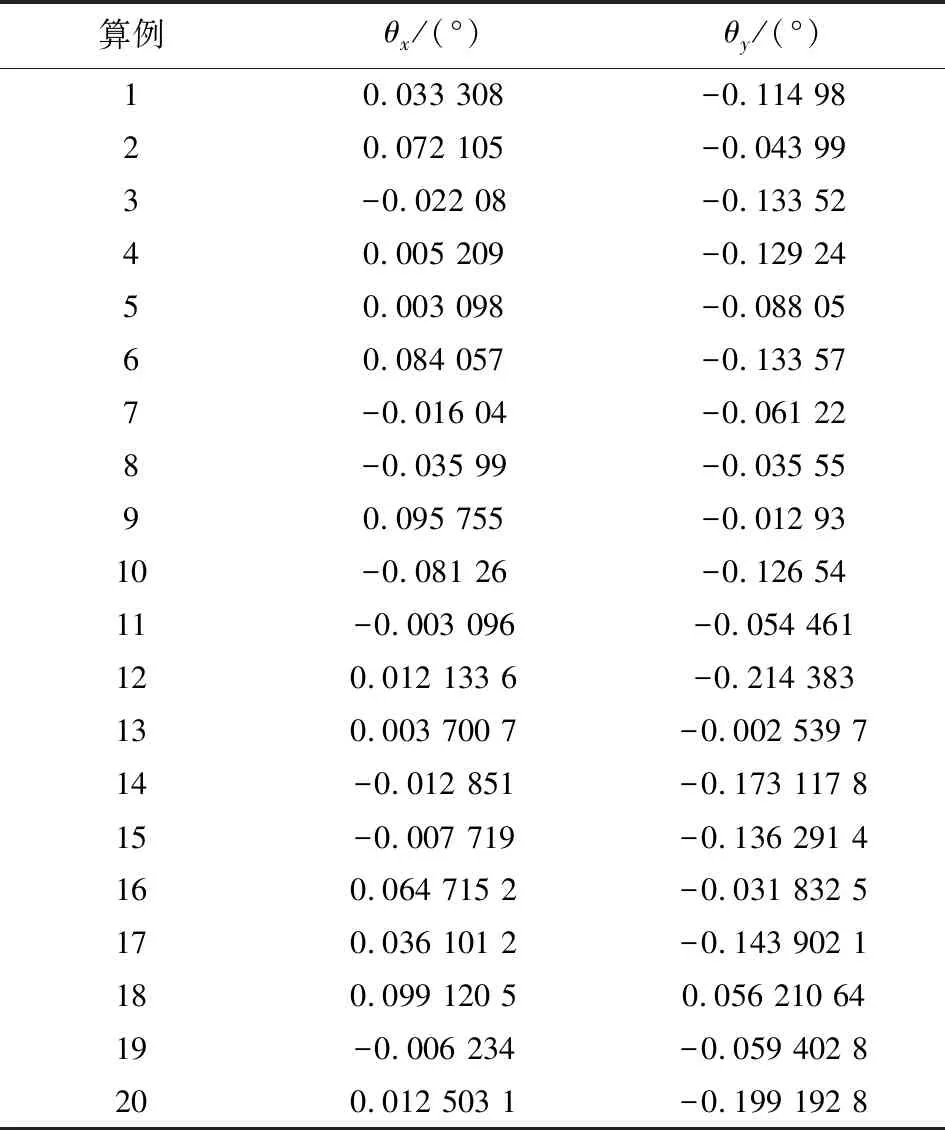
表5 弹/枪相互作用模型计算结果
2.3 外弹道计算结果
通过内弹道模型的20组随机抽样计算,可得到弹丸初速的散布,如表4所示;通过弹/枪相互作用模型的20组数值模拟结果,可以得到弹丸出膛时的质心速度偏角的散布,如表5所示。将随机内弹道模型和弹/枪相互作用模型的计算结果传递到外弹道模型,在相关参数的散布范围内,采用MATLAB自编软件进行外弹道的计算,可得到枪械在一定距离处的立靶射弹散布。计算所得100 m立靶处的3组(每组20发)射弹散布仿真结果及散布圆(R50和R100)如图6(a)~6(c)所示,图中,Y和Z分别为弹着点在立靶上垂直和横向的坐标。
2.4 仿真与实验结果的对比
为了验证仿真结果的正确性,进行了实弹射击的验证。协同仿真法对射弹散布的预测与实验结果的对比如表6所示,结果表明,协同仿真法能够较好地预测枪械的射弹散布,仿真结果R50和R100与实际射击结果平均相对误差分别为13%和8%,绝对误差小于1 cm。
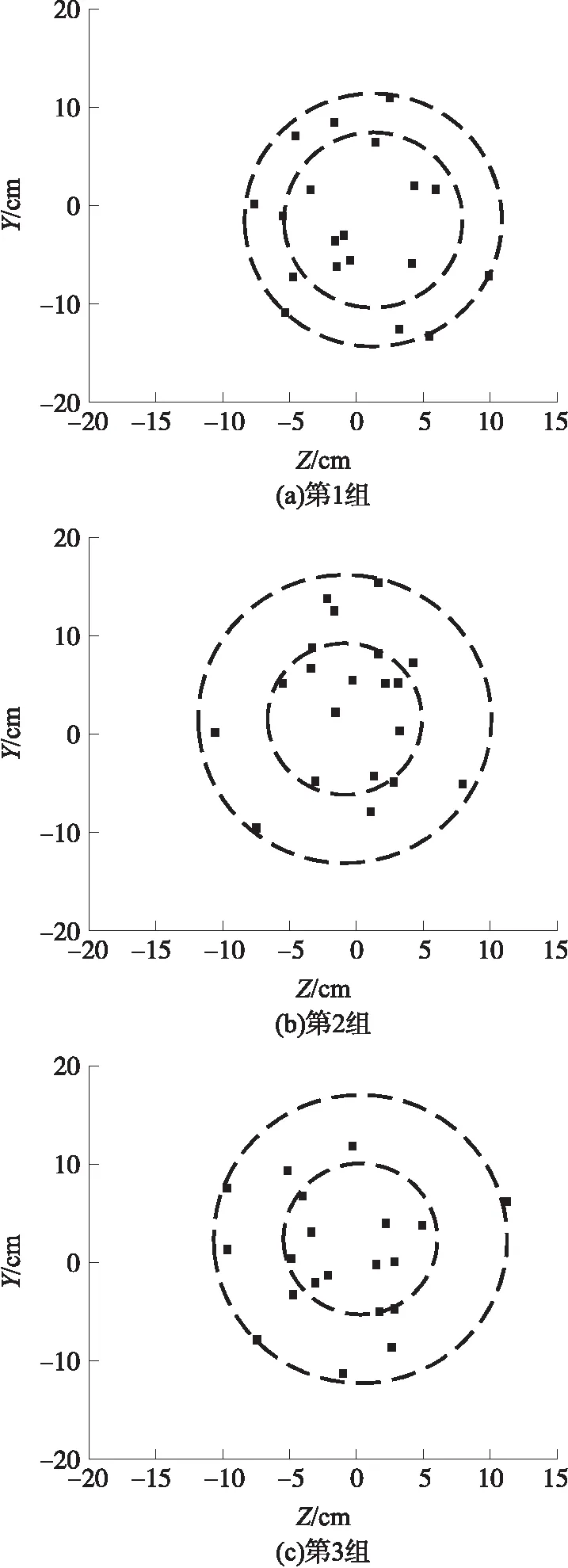
图6 100 m立靶处射弹散布仿真结果

R50/cm第1组试验仿真第2组试验仿真第3组试验仿真R50/cm试验仿真4.96.85.25.85.75.55.36R100/cm第1组试验仿真第2组试验仿真第3组试验仿真R100/cm试验仿真10.89.511.51112.21111.510.5
3 结论
本文提出了一种枪械射弹散布的预测方法,该方法在枪械随机内弹道模型、弹/枪相互作用模型和外弹道模型的基础上,通过各模型之间的协同仿真进行参数传递,实现了整个射击过程的仿真模拟。通过引入误差源,模拟了实际射击过程中的随机因素,从而预测枪械射弹散布。本文提出的枪械射弹散布预测方法,为发展面向射击精度的设计理论奠定了基础。
