导气式步枪单发精度仿真分析方法
2019-09-25苑大威沙金龙王雪皎
苑大威,沙金龙,王雪皎
(1.瞬态冲击技术重点实验室,北京 102202;2.中国兵器工业第208研究所,北京 102202)
目前步枪射击精度指标主要靠试验获取,现有的射击精度仿真分析方法大多只考虑枪弹因素,无法在设计初期仿真分析精度指标,缺乏一种行之有效的射击精度仿真分析方法用以指导设计。
随着仿真技术的发展,研究人员相继开展了枪械射击精度仿真分析,李涛等[1-2]仿真分析了射频、发射动力学对射击精度的影响,王兆胜等[3-4]从试验的角度分析了枪械射击精度的影响因素、表征方法。上述仿真分析因素较为单一,需要进行更加系统、深入的研究。
本文主要研究固定架状态步枪的单发射击精度,研究中排除了人体因素的影响。本射击精度仿真分析方法基于随机内、外弹道方程,结合仿真分析,在考虑全枪和弹药结构及参数的基础上,研究影响射击精度的随机因素,在立靶散布上,获得规定射程处R50、R100值(R50为半数弹着圆半径,R100为全数弹着圆半径),该方法可以用于指导枪械结构优化设计,达到提高射击精度的目的。
1 射击精度仿真分析方案
本文单发射击精度仿真分析的具体方案为:将初速误差、弹形系数误差、射角误差(包括横向及纵向射角)等影响步枪射击精度的因素融入到随机外弹道方程[5](本研究聚焦枪械结构因素的影响,暂不考虑后效期影响产生的起始扰动和气动跳角)。其中,弹形系数误差来自加工尺寸公差要求;初速误差来源于影响内弹道的装药量、弹丸质量、药室容积、启动压力等随机因素,通过融入随机内弹道方程计算获得;横向及纵向射角误差主要通过仿真分析提取,并进行试验验证;最终针对4个误差变量建立概率密度函数数学模型,并输入到随机外弹道方程,可仿真分析出枪械射击精度,获得100 m处R50和R100值,并进行试验验证。方案流程如图1所示。

图1 导气式步枪射击精度仿真分析方案
2 弹丸初速误差分析计算
弹丸初速误差主要来源于影响内弹道的随机因素,包括:装药量mc、弹丸质量mp、药室容积V、启动压力p0[6-7]。将这些随机量融入内弹道方程,建立随机内弹道数学模型,设随机变量X服从正态分布,即X~N(μ,σ2),概率密度函数:
(1)
则随机量正态分布概率模型可用x=σ+μ得到,其中各随机变量的均值为名义数值,标准差来自实际加工或工艺误差,如表1所示。

表1 内弹道随机变量
将这些随机因素生成1 000组的组合作为随机内弹道仿真的输入,求解得到如图2、图3所示的最大膛压及弹丸初速的随机分布,图中,ε为射弹数,最大膛压均值为310 MPa,标准差为25 MPa;弹丸初速均值为910 m/s,标准差为20 m/s。
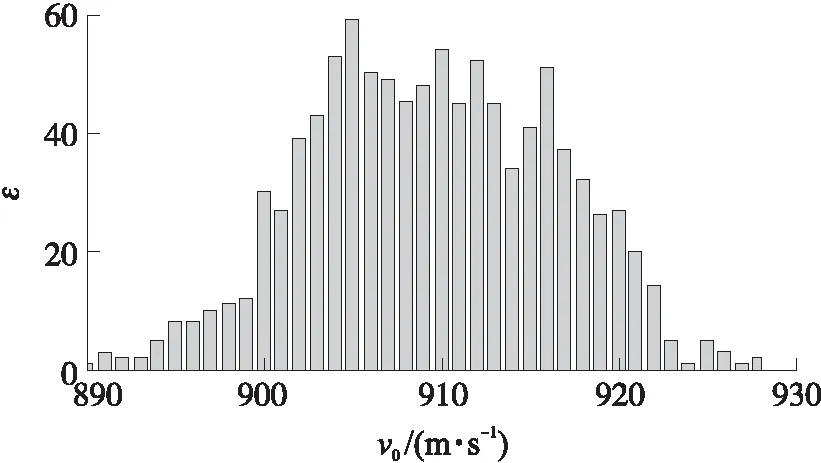
图2 初速随机分布

图3 膛压随机分布
假设:①火药燃烧服从几何燃烧定律;②弹丸运动在平均压力下进行;③膛壁热散失忽略不计;④火药燃烧生成物成分始终不变。内弹道方程如下:
(2)
式中:χ,μ为火药形状特征量;ψ为火药已燃百分比;Ik为火药燃烧结束瞬间压力全冲量;φ为次要功系数;t为火药燃烧时间;tq为弹丸经过导气孔的时间;α为余容;lψ为药室容积缩径长;ζ=k-1,k为绝热系数;B为时间参数;l为弹丸行程;β为导气室结构参数;pq为导气室压力;pφ为弹丸经过导气孔瞬间膛内火药气体压力;n为燃速指数;μ1为燃速系数;e1为弧厚;e为药粒已燃厚度;v为弹丸速度;p为平均压力;Z为火药已燃相对厚度;S为枪膛截面积;f为火药力。
3 射角误差仿真分析
射角误差主要来源于枪管的振动和角位移,弹丸出枪口时枪管轴线与发射前产生一个小的角度。引起射角误差的主要原因包括自动机运动和导气压力作用,可采用仿真的方法分析枪口的跳动量和位移量。
3.1 自动机运动下枪口跳动量分析
通过多体动力学软件[8]分析全枪机构动作,仿真模型如图4所示。枪托和护手设置固定约束,膛底施加膛压曲线,采用刚柔耦合的方法将枪管柔性化,获得枪口跳动量值,枪口横向最大跳动量为0.02 mm,枪口纵向最大跳动量为0.08 mm。

图4 全枪机构运动引起枪口跳动的仿真模型
3.2 导气压力作用下枪口偏移量仿真分析
膛压存在的跳差导致导气室压力也存在跳差,经布拉文公式计算,导气室压力峰值为66 MPa,跳差为±8 MPa,通过仿真分析,导气室压力作用下枪口位移量为1.54 mm,跳差为±0.4 mm,如图5所示,图中,s为枪口纵向位移,位移曲线如图6所示。

图5 导气室压力作用下枪口偏移量仿真
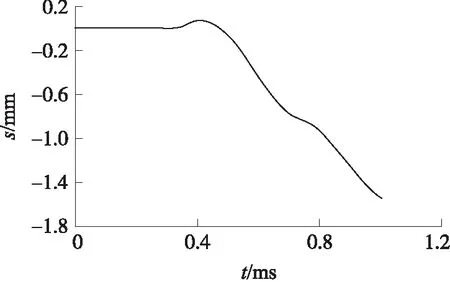
图6 导气室压力作用下枪口偏移量曲线
3.3 弹丸挤进作用下枪口偏移量仿真分析
在弹丸与枪管实际装配位置的弹丸尾部施加膛压曲线,弹丸枪管全部划分成六面体网格,如图7所示。仿真分析弹丸挤进枪管全过程中弹丸和枪口的运动规律,枪口最大位移量为0.001 mm,虽然变化明显,但是由于数量级太小,转换到枪管射角变化,基本为0。实际上弹丸挤进枪管的过程中,枪管受力是轴对称的,没有使枪管径向运动的力。

图7 弹丸挤进枪管仿真模型
3.4 枪口纵向跳角
纵向跳角θ可由图8计算得出,弹尖处的偏差可近似等于枪口位移量与全枪机构动作引起的枪口跳动量之和,枪口位移量为自动机运动及导气室压力作用2个仿真位移量之和,则θ=arctan(1.63/120)=0.78°,跳差为±0.2°。
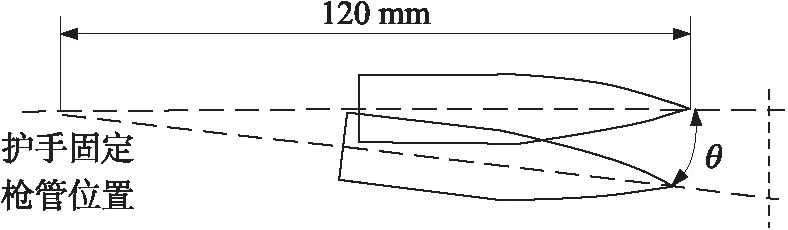
图8 枪口纵向跳角
4 立靶散布仿真分析模型的建立
立靶散布偏差通常包括纵向偏差和横向偏差。本文建立在初速、射角影响下的射弹立靶散布统计模型,分析枪弹外弹道散布特性。
确定影响射弹立靶散布的随机因素,这些因素包括:初速v0、纵向跳角θz、横向跳角θh、弹形系数i。设随机因素服从正态分布,弹丸初速均值及标准差来自随机内弹道计算结果,跳角均值及标准差来自仿真结果,弹形系数均值及标准差来自设计要求及经验,将这些因素随机生成20组的组合,作为随机外弹道仿真的输入。外弹道随机变量见表2。

表2 外弹道随机变量
本文重点研究枪械因素对射击精度的影响,采用质点外弹道方程,通过循环调用质点外弹道计算程序进行20发随机外弹道仿真计算,求出4种随机因素下的20发落点坐标并保存,生成立靶散布图,并求出平均弹着点R50,R100。3组100 m处立靶散布如图9所示。
质点外弹道方程采用四阶龙格库塔方法解算,并用C++Builder软件开发建立解算程序。
考虑气温、气压非标准的影响,不考虑地球曲率及科氏加速度的影响,质点弹道方程为
(3)
式中:c为弹道系数,H(y)为空气密度函数,G(v,cs)为阻力函数。

图9 立靶散布图(X=100 m)
5 试验验证
试验以某自动步枪为研究对象,将枪托和护手夹持固定,如图10所示,射击距离100 m,目标为胸环靶。在枪口附近进行高速摄影,见图11,拍摄弹丸出枪口瞬间纵向跳动情况,获取枪口纵向位移s,如表3所示。

图10 枪械射击试验图

图11 弹丸出枪口瞬间

序号s/mm试验仿真12345-1.22-1.89-1.22-1.83-1.871.54均值-1.611.54
分别进行3组射击,每组20发,获取胸环靶射击结果,如图12所示,计算得出R50,R100,与仿真结果对比分析,如表4所示。计算可得,仿真结果:σR50=0.29 cm,σR100=2.55 cm;试验结果:σR50=0.45 cm,σR100=4.42 cm;仿真与试验均值的相对误差:rR50=2%,rR100=13.9%。

图12 胸环靶射击结果
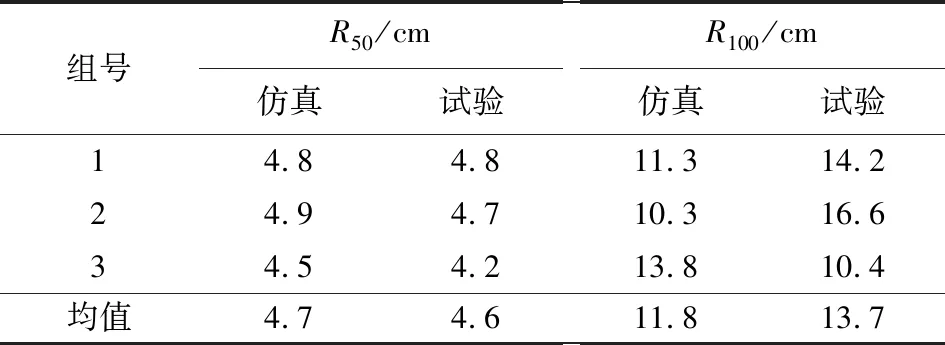
组号R50/cm仿真试验R100/cm仿真试验14.84.811.314.224.94.710.316.634.54.213.810.4均值4.74.611.813.7
6 结论
本文基于多体动力学仿真、结构力学仿真、随机内、外弹道方程,建立了导气式枪械射击精度仿真分析模型,初步预测了100 m处的R50,R100,并进行试验验证,得到如下结论:
①经对比分析,该枪械枪口偏移量仿真与试验相对误差、R50均值相对误差、R100均值相对误差均小于15%,说明该技术可用于新型枪械研制中的精度分析。
②本文聚焦于步枪本身对单发射击精度的影响,尚未充分考虑枪弹因素,如枪弹攻角变化以及后效期膛口流场的影响。本文方法可以分析枪械零部件(如上、下机匣)的公差配合对射击精度的影响,具有一定的工程应用价值。
