基于自适应容积卡尔曼滤波的交互多模型算法
2019-09-24杜云张静怡
杜云 张静怡


摘 要:ADS-B航迹处理主要包括航迹数据滤波和滤波后数据可靠性的判断。飞机飞行运动复杂,而报文需要在飞行过程中向外界发送,此时报文会受到来自外界的影响和干扰,从而使航迹信息出现误差或丢失。为提高ADS-B航迹报文的准确性,文章采用了交互多模型滤波算法,将自适应容积卡尔曼滤波器作为交互多模型滤波算法的滤波器,并将当前统计模型作为交互多模型的子模型。仿真结果表明,论文改进的算法提高了滤波算法的滤波性能,相较于传统的交互多模型滤波算法具有更高的滤波精度。
关键词:航迹滤波;当前统计模型;交互多模型;自适应容积卡尔曼滤波算法
中图分类号:O159 文献标志码:A 文章编号:2095-2945(2019)25-0022-04
Abstract: ADS-B track processing mainly includes track data filtering and judgment of data reliability after filtering. The flight motion of the aircraft is complex, and the message needs to be sent to the outside world during the flight. At this time, the message will be affected and disturbed by the outside world, resulting in the error or loss of track information. In order to improve the accuracy of ADS-B track message, the interactive multi-model filtering algorithm is adopted, and the adaptive volume Kalman filter is used as the filter of interactive multi-model filtering algorithm. The current statistical model is regarded as a submodel of the interactive multi-model. The simulation results show that the improved algorithm improves the filtering performance of the filtering algorithm, and has higher filtering accuracy than the traditional interactive multi-model filtering algorithm.
Keywords: track filtering; current statistical model; interactive multiple model; adaptive volume Kalman filtering algorithm
廣播式自动相关监视(Automatic Dependent Surveillance-Broadcast),简称ADS-B[1]是一种协同监视技术。ADS-B报文产生的精准航迹信息是航空管制的数据依据,报文的丢失或错误,目标运动状态的改变都会导致目标跟踪算法精度降低或发散;环境的变化引起过程噪声和观测噪声统计性能变化;目标运动模型的非线性会引起模型误差。这就需要通过滤波的方法对数据进行预测和修正,使航迹更加准确。提高滤波算法的滤波精度、自适应能力、与目标运动模型匹配度,能够减少误差,获得更好的性能。文献[2]采用经典的交互多模型算法,滤波器和运动模型集选取都较为基础,所以滤波精度不理想[2]。文献[3]采用交互多模型算法,对直线运动模型具有很好地滤波精度,对其他运动模型效果不佳[3]。文献[4]将“当前”统计模型和修正转弯模型作为交互多模型算法的模型集,增强了算法的自适应能力[4]。本论文将自适应容积卡尔曼滤波算法与交互多模型算法相结合,用自适应容积卡尔曼滤波器代替卡尔曼滤波器,进一步提高了滤波算法的滤波性能,相较于传统的IMM滤波算法具有更高的滤波精度。
1 目标运动系统模型
首先建立系统模型来描述飞机的运动状态,就是把飞机的运动状态抽象成两个数学模型:状态模型和量测模型。该方法把某一时刻系统状态描述为前一时刻的系统状态的函数,系统的输入输出用状态转移模型和输出量测模型表示。飞机离散时间系统的状态方程和量测方程分别表示为:
其中,W(k)为k时刻系统的过程噪声,X(k)为k时刻的状态,F(k)为状态转移矩阵,?祝(k)为噪声转移矩阵,H(k)为观测矩阵,V(k)为观测噪声。
2 自适应容积卡尔曼滤波算法
2.1 容积卡尔曼滤波算法
由Arasaratnam等人提出的容积卡尔曼滤波算法(CKF)是新兴的一种非线性滤波算法,其核心是采用三阶球面-相径容积规则近似非线性函数传递的后验均值和协方差,有强大的数学理论作支撑[5,6]。相较于较为常用的扩展卡尔曼滤波算法[7]和无迹卡尔曼滤波算法[8]其计算量更小,精度更高。从CKF的实施流程来看,其数学理论严谨,参数选取方便,收敛效果好,设计方法简洁,需要调节的参数较少,所以该算法自被提出,就受到了广泛的关注。
CKF算法需要计算容积点,而后利用2n个容积点进行加权求和来近似高斯积分,对于解决任意分布函数利用容积积分准则求解积分问题,可以表示为:
式中,表示正态分布,其均值为?滋、协方差为P,?棕i表示容积点的权值,?孜i表示传播的容积点集,L表示等权容积点数。
CKF算法的实现步骤为:
时间更新
已知k-1时刻的状态xk-1误差协方差为Pk-1,对Pk-1做Cholesky分解,
选择容积点为:
经系统传递后的容积点:
k时刻的状态预测值:
k时刻的误差协方差:
量测更新
对Pk|k-1做Cholesky分解:
计算容积点:
通过测量方程传递容积点:
估计k时刻的观测预测值:
估计k时刻量测误差协方差:
估计k时刻一步预测相关协方差:
估计k时刻滤波增益:
求取k时刻状态估计更新值:
求取k时刻状态误差协方差估计值:
2.2 自适应卡尔曼滤波算法
在实际情况中,由于外界环境的复杂性,量测误差就会改变,但是当量测误差协方差矩阵Rk一直用固定的初始值,容积卡尔曼算法就不能根据环境的变化进行自我调整。因此,对容积卡尔曼算法进行自适应改进。
新息序列为:
新息协方差矩阵为:
用新息样本数据对新息协方差矩阵进行近似估计
其中,L表示样本数据个数。结合卡尔曼滤波算法中量测误差协方差,Rk可以表示为:
(21)
3 基于自适应容积卡尔曼滤波的交互多模型算法
交互多模型滤波(IMM)算法是一种软切换算法,目前在机动目标跟踪领域得到了广泛的应用[9,10]。IMM算法使用两个或更多的模型来描述工作过程中可能的状态,最后通过有效的加权融合进行系统状态估计,很好地克服了单模型估计误差较大的问题。IMM算法采用的是多个卡尔曼滤波器进行并行处理。但处理后的精度效果不理想,所以论文用自适应容积卡尔曼滤波器代替卡尔曼滤波器。基于自适应容积卡尔曼滤波的交互多模型算法的步骤如下:
步骤1.输入交互
由目标的状态估计 与每个滤波器的模型概率?滋j(k-1)得到混合估计 和协方差 ,将混合估计作为当前循环的初始状态。具体参数计算如式(26)
预测概率(归一化常数)为:
混合概率为
混合状态估计为:
混合协方差估计为:
式中,Pij模型i到模型j的转移概率;?滋j(k-1)为模型j在k-1时刻的概率。
步骤2:自适应容积卡尔曼滤波
使用混合估计作为单个滤波器的输入用自适应容积卡尔曼滤波进行预测和更新步骤,按照式(3)~(21),得到残差,残差协方差和协方差。
步骤3:模型概率更新
第j个模型的似然函数为:
模型j的概率为:
其中,c为归一化常数,
步骤4:输出交互
IMM估计量的总体估计量以单个滤波器估计量的加权和计算,即
4 仿真结果及分析
选择匀速运动模型、匀加速运动模型及“当前”统计模型作为算法的模型集。k时刻目标状态向量为Xk=[x ■ ■ y ■ ■]T,分别为x和y方向的位置、速度和加速度。假设目标初始条件为X0=[10000 0 0 2000 -15 0]。目标在400s~600s向x轴慢转弯,x方向和y方向的加速度为0.08m/s,转弯结束后加速度降成零,从610s开始做快转弯运动,加速度为0.3m/s2。控制模型转换的马尔科夫链的转移概率矩阵为
设定各模型在此时刻的概率分别为?滋=[0.4 0.3 0.3],采样周期T=2s,量测噪声是均值为0、标准偏差为100m的高斯序列。
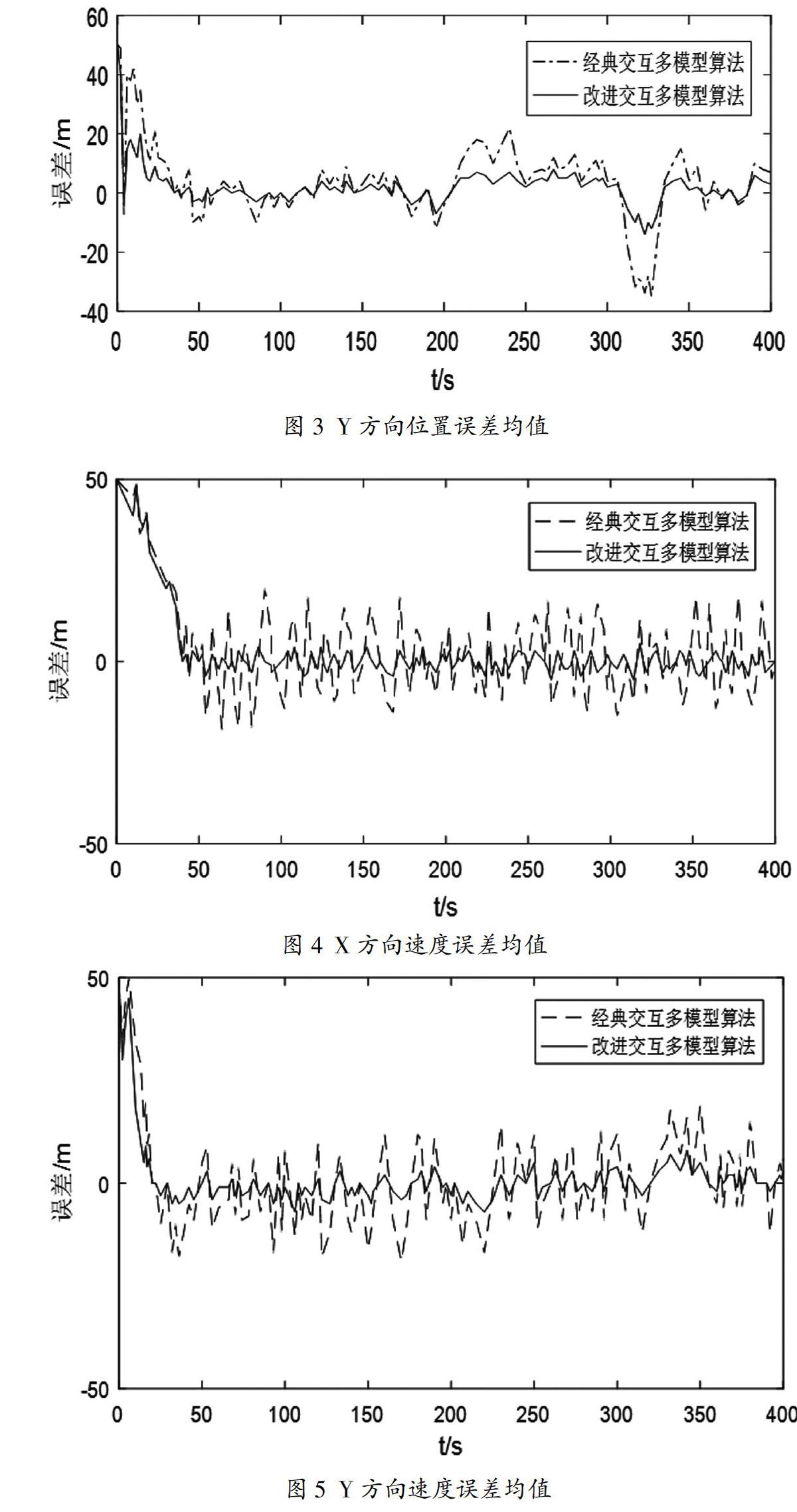
图2和图3表示的是经典交互多模型算法和基于自适应容积卡尔曼滤波的交互多模型算法在X方向和Y方向上的位置误差均值,从图中可以看出基于自适应容积卡尔曼滤波的交互多模型算法的误差均值整体要小于经典交互多模型算法。
图4和图5表示的是经典交互多模型算法和基于自适应容积卡尔曼滤波的交互多模型算法在X方向和Y方向上的速度误差均值,从图中可以看出基于自适应容积卡尔曼滤波的交互多模型算法的速度误差均值整体要小于经典交互多模型算法。
5 结束语
本文研究的算法将自适应容积卡尔曼滤波算法作为交互多模型滤波算法的滤波器,自适应能力减少了误差,获得了更好的性能,并将“当前”统计模型作为交互多模型算法的模型集,提高了滤波算法的滤波精度。仿真结果表明,基于自适应容积卡尔曼滤波的交互多模型算法要优于经典交互多模型算法。
参考文献:
[1]陈蕾,吴仁彪,卢丹.利用多普勒效应的ADS-B欺骗式干扰检测方法[J].信号处理,2018,6(11):722-728.
[2]张朝柱,杜瑞敏.IMM算法的高机动目标航迹滤波在ADS-B中的應用[J].应用科技,2016,43(5):24-29.
[3]翟海涛.基于IMM模型的目标跟踪算法[J].中国制造业信息化,2010,39(13):61-63.
[4]王尔申,翟秋刚,徐嵩,等.基于改进交互式多模型算法的ADS-B航迹滤波方法研究[J].电光与控制,2018(07).
[5]Arasaratnam I, Haykin S.A numerical-integration perspective on Gaussian filters[J]. IEEE Transactions on Automatic Control, 2009,54(8):1254-1269.
[6]Nielsen R O. Accuracy of angle estimation with monopulse processing using two beams [J]. Aerospace & Electronic Systems IEEE Transactions on,2001,37(4):1419-1423.
[7]Einicke G A,White L B. Robust extended Kalman filtering[J].Signal Processing IEEE Transactions on,1999,47(9):2596-2599.
[8]Julier S J,Uhlmann J K. Unscented filtering and nonlinear estimation [J]. Proceedings of the IEEE,2004,92(3):401-422.
[9]GAO L, XING J P, MA Z, et al. Improved IMM algorithm for nonlinear maneuvering target tracking [J]. Procedia Engineering, 2012(29):4117-4123.
[10]YUAN G,ZHU W, WANG W, et al. Maneuvering target tracking algorithm based on interacting multiple models[J].Mathematical Problems in Enginerring,2015,2015(5):1-7.
