基于“四能”的学习内容开发与实践①
——以“三角形分割为两个等腰三角形”的探究为例
2019-09-24伍春兰
张 勃 伍春兰
(北京市房山区良乡第二中学 102488; 北京教育学院数学系 100120)
《义务教育数学课程标准(2011年版)》提出了“运用数学的思维方式进行思考,增强发现和提出问题的能力、分析和解决问题的能力”的“四能”总目标. 《普通高中数学课程标准(2017年版)》也提出了“提高从数学角度发现和提出问题的能力、分析和解决问题的能力”的“四能”课程目标. 因此,在核心素养大背景下,如何基于学生“四能”的提升,开发学习内容并实施是值得深入研究的.
下面以“三角形分割为两个等腰三角形”的探究为例,阐述我们的实践与思考.
1 三角形分割
任意一个三角形都可以从一个顶点引出一条射线与对边相交,顶点与交点之间的线段(分割线)把三角形分割成两个小三角形. 但是如果分割后的小三角形是特殊的,则被分割的三角形就要有一定的条件限制. 探讨何种三角形分割后符合目标定位的小三角形,或者已知的三角形分割后是否存在符合目标定位的小三角形,可以考量学生的思维品质,以及分析问题、解决问题的能力. 因此近年(模拟)中考,涉及三角形分割的试题数见不鲜.
比如,2014年南京市建邺区中考数学一模27题,将三角形分割为一个等腰三角形和一个直角三角形,称分割线为伴侣分割线,并探讨伴侣分割线存在的三角形角度的关系. 再如,2016年宁波市中考数学25题,将三角形分割为一个等腰三角形和一个与原三角形相似的三角形,称分割线为完美分割线,并证明或求解与完美分割线相关的问题. 又如,2016宁波市北仑区中考一模25题,将三角形分割为两个等腰三角形,称分割线为特异线,并证明或求解与特异线相关的问题.
特异线存在的经典三角形有两类,一类是黄金三角形(顶角为36°或108°的等腰三角形),因其腰与底之比成黄金比而得名. 有趣的是分割后得到的两个小三角形不仅还是黄金三角形(其中一个与原黄金三角形相似,见图1和图2),而且分割线将对边分割成黄金比的线段. 另一类是直角三角形,由“斜边中线等于斜边一半”的定理,易证明结论的正确.

图2
文献[1]证明了非直角三角形可分割为2个等腰三角形的充要条件是: 有两个内角之比为1∶2或1∶3,而且这两角中的较小者小于π/4.
2 文献分析
对于分割成两个等腰三角形的三角形,文献[2-4]都采用了分类的方式详细探讨. 文献[2]按三角形三个角的关系:3个角相等、2个角相等(顶角小于底角;顶角大于底角)、3个角都不相等的三角形分类探索;文献[3]先按角将三角形分类,再按三角形最小角为分割后的小等腰三角形的顶角、底角分类探究;文献[4]按三角形类型(直角三角形、一般三角形、等腰三角形)分类探讨. 上述文献虽然结论还不完备,但逻辑还是清楚的.
一些教师以“三角形分割为两个等腰三角形”为主题尝试课堂教学,从问题解决[5]、数学活动课[6]、积累数学活动经验[7]、支架式教学理论指导[8]等视角积极探索,为相关内容的教学提供了经验.
3 教学实践
3.1 第一次教学实践
3.1.1引出猜想
教师通过创设情境或提出问题(见表1),使学生明确了研究方向,猜想出具有2倍角、3倍角关系的一般三角形可以分割为两个等腰三角形.

表1 教师创设的情境或提出的问题
3.1.2初步验证
师:请自己设计一个三角形,使这个三角形可以被分割成两个等腰三角形.先独立思考,然后小组合作.
教师让完成的小组把分割成两个等腰三角形的三角形内角度数写在黑板上,并引导学生发现角之间的关系并归类(见表2).

表2 学生小组列举可分割等腰三角形的三角形
3.1.3探索条件
师:刚才有小组发现,具备2倍角关系的三角形也有的不能分割成两个等腰三角形,比如三个内角分别是50°、100°、30°的三角形.问题是哪些三角形可以被分割成两个等腰三角形?
师:在△ABC中,设∠A=α,∠B=β,∠C=γ(α>β)(图4),当α,β,γ满足什么数量关系时,△ABC可以被分割成两个等腰三角形?
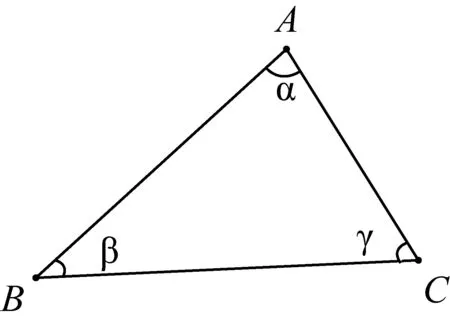
图4

图5
师:因为α>β,作∠BAD=β(图5),这样就构造了一个等腰三角形△ABD. 欲使△ADC也是等腰三角形,要满足什么条件?
生:只需△ADC有两个角相等,分类讨论.
(1)若∠ADC=∠C,则γ=2β;
(2)若∠ADC=∠DAC,则α-β=2β,有α=3β;
(3)若∠DAC=∠C,则α-β=γ,有α=β+γ.
师:情形(1)、(2)得到的结论,说明能分割成两个等腰三角形的三角形,具有2倍或3倍角关系. 前面遇到过有2倍角关系的三角形,但不能分割成两个等腰三角形,因此还要深入探究角的其它限制条件.
当γ=2β,因为α>β,所以180°-β-2β>β,解得β<45°;当α=3β,因为γ>0°,所以180°-β-3β>0°,解得β<45°.于是得到以下结论:当1倍角小于45°时,有2倍角、3倍角关系的三角形可分割成两个等腰三角形.
师:α=β+γ,这是什么特征的三角形?
生:直角三角形.
师:直角三角形如何分割成两个等腰三角形?
生:利用斜边中线分割.
3.2 第二次教学实践
3.2.1问题的提出
学生经历黄金三角形(顶角为36°)的分割为两个等腰三角形后,教师引导学生尝试提出相关问题,结果他们基本上提出了预设的问题(见表3),不过也没有超出预设的范围.
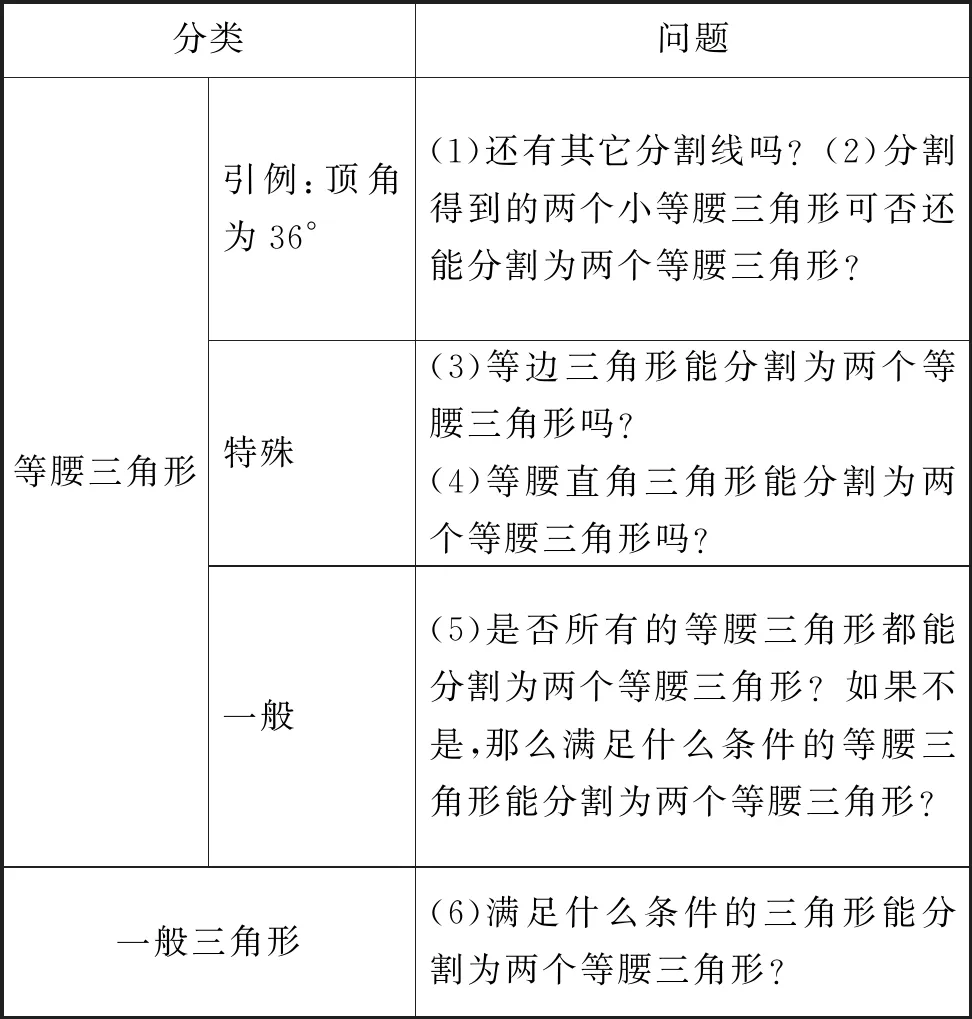
表3 学生尝试提出相关问题归类(预设)
3.2.2等腰三角形的分割探究

图6
尝试对问题(3)(等边三角形)的分割未果,学生发现不是所有的等腰三角形都能分割为两个等腰三角形.
对引例和问题(2)的分割,学生体会到:不能分割最小角;顶角是锐角和钝角时,分割的角是不一样的. 于是在分析满足什么条件的等腰三角形能分割为两个等腰三角形时,学生认为需要分类讨论:顶角为锐角(见图6)、直角(已解决)及钝角(见图7). 经过探究,学生发现:只有顶角是36°、180°/7、90°及108°的等腰三角形,才能分割为两个等腰三角形.

图7
3.2.3一般三角形的分割探究
4个能分割的等腰三角形,除了有两个角相等,学生发现还有两个角具备2倍或3倍的关系,提出猜想:具有2倍或3倍角的关系的一般三角形,可能分割为两个等腰三角形. 为了验证猜想,按照特殊到一般的原则,教师引导学生挑选具备2倍或3倍角的关系的特殊三角形(见表4),然后尝试分割积累活动经验,最后探究一般三角形分割成两个等腰三角形的条件.
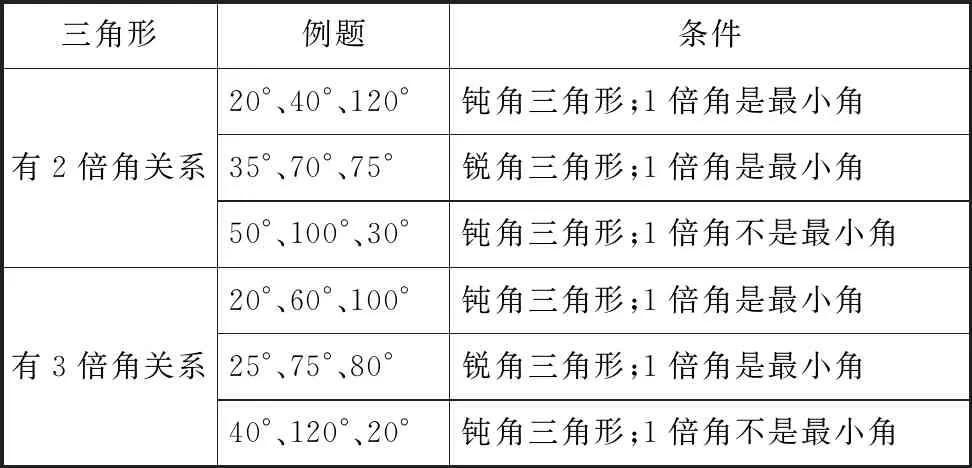
表4 具备2倍或3倍角的关系的三角形(举例)
4 思考建议
4. 1 “四能”的培养既需要活动经验的支撑,更需要理性思考的融入
学生在本节课学习之前,对三角形的分割是有体验的. 比如中线将三角形分割为2个等(面)积三角形,高线可将三角形分割为2个直角三角形. 换个角度观察中线、高线,不仅对这两个重要线段有了新的认识,也唤起了学习本节课的活动经验.
专题课是一种普遍教学形态,教师往往将同一类考(习)题聚在一起组成一个专题,旨在学会解决这类问题的套路. 学生缺少题目来龙去脉的考察,题目之间关联的分析,以及思想方法的感悟. 因此,将一个特殊问题变式为一类问题的专题课,在日常教学中并不多见. 所以三角形分割的第一次教学实践,得到很多观摩教师的好评. 但我们也发现一些不足,主要是学生的思维参与欠缺.
在第二次教学实践中,学生两次经历了从特殊到一般的探究,特殊情形的分割,不仅让学生发现、提出了问题,也为分析、解决问题提供了方向. 同时,第一次从特殊到一般的探究(等腰三角形的分割)为第二次探究(一般三角形的分割)提供思路和方法. 在整个活动中思考贯穿始终,并在活动前后通过交流促进学生思考. 作为延拓,鼓励学生就三角形分割,发现、提出新的研究问题(作为作业),比如,研究三角形分割为一个等腰三角形和一个直角三角形的条件,并分析解决问题.
4.2 教师要成为学习资源的研究者和开发者
教师通过对典型问题的多角度的审视与探究,将适宜学生学习的、富含数学思维价值的资源开发成教学内容. 经历生成式的探究教学,实现巩固“四基”、感悟思想、获得经验的近期目标,也为提升“四能”、涵养核心素养的远期目标“添砖加瓦”.
4.3 信息技术成为探究教与学的工具
非直角三角形分割为2个等腰三角形,当两个内角之比为1∶2或1∶3时,许多研究者(教师)都忽略了“较小者小于π/4”这个条件,包括已发表的研究成果. 事实上这个条件对初中生也是不易发现的,所以师生借助动态软件启发思考,突破难点是非常有裨益的. 比如,两个内角之比为1:2(∠A:∠B)的三角形,分别从顶点C(见图8)、顶点B(见图9)引分割线,利用滑动条的变动,感受∠A范围的限制. 当从顶点C分割时,∠A需要小于45°;当从顶点B分割时,∠A只能等于45°(见图10)或等于36°(见图11). 当然动态课件的嵌入,既可作为理性证明后的直观演示,也可作为理性思考前的合理猜想,还可作为理性与直观交互思考的媒介. 因此何时、怎样融入信息技术,需要教师根据教学目标与学情抉择.

图8
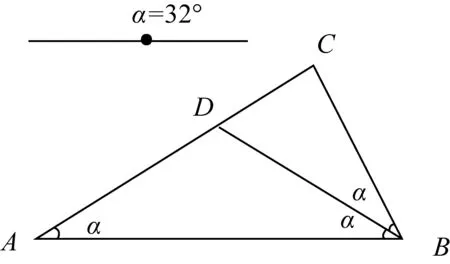
图9

图10

图11
4.4 “四能”成为核心素养落地的现实力量
目前课程构建、开发与实施都声称基于核心素养的,然而实际上有些与“核心素养”立意存在较大的出入. 因此以课程为载体,在构建、开发与实施过程中,以“四能”为抓手是促进核心素养落地的有效途径.
